
Concept explainers
Refer to the Buena School District bus data.
- a. Suppose we consider a bus “old” if it has been in service more than 8 years. At the .01 significance level, can we conclude that less than 40% of the district’s buses are old? Report the p-value.
- b. Find the
median maintenance cost and the median age of the buses. Organize the data into a two-by-twocontingency table , with buses above and below the median of each variable. Determine whether the age of the bus is related to the amount of the maintenance cost. Use the .05 significance level. - c. Is there a relationship between the maintenance cost and the manufacturer of the bus? Use the breakdown in part (b) for the buses above and below the median maintenance cost and the bus manufacturers to create a contingency table. Use the .05 significance level.
a.
Check whether one can conclude that less than 40% of the district buses are old.
Find the p-value.
Answer to Problem 64DE
It cannot be concluded that less than 40% of the district buses are old.
The p-value is 0.181.
Explanation of Solution
Let
The null and alternative hypotheses are stated as follows:
The sample proportion of the old buses can be obtained as follows:
Thus, the sample proportion of the old buses is 0.35.
The sample size n is 80 and
Step-by-step procedure to find the test statistic using the MINITAB software:
- Choose Stat > Basic Statistics > 1 Proportion.
- Choose Summarized data.
- In Number of events, enter 28. In Number of trials, enter 80.
- Enter Hypothesized proportion as 0.40.
- Check Options, enter Confidence level as 99.0.
- Choose less than in alternative.
- Select Method as Normal approximation.
- Click OK in all dialogue boxes.
Output is obtained as follows:

Thus, the value of the test statistic is –0.91and the p-value is 0.181.
Decision rule:
If the p-value is less than the significance level, reject the null. Otherwise, fail to reject the null hypothesis.
Conclusion:
The significance level is 0.01 and the p-value is 0.181. Here, the p-value is greater than the significance level 0.01. By the rejection rule, fail to reject the null hypothesis.
Therefore, one cannot conclude that less than 40% of the district buses are old.
b.
Find the median maintenance cost.
Find the median age of the buses.
Construct a two-way contingency table for the maintenance cost and age of the buses.
Check whether there is a relationship between the age of the buses and maintenance cost.
Answer to Problem 64DE
The median maintenance cost is $456.
The median age of the bus is 4.5 years.
The age of the bus is related to the amount of the maintenance cost.
Explanation of Solution
The median maintenance cost for the bus is calculated as follows:
First, arrange the data into ascending or descending order and then, find the median for the maintenance cost. Since there is even number of observations in the maintenance cost variable, the median is the average of the 40th and 41th observations. That is,
Thus, the median maintenance cost is $456.
The median age of the bus can be obtained as follows:
First, arrange the data into ascending or descending order and then, find the median of the bus. Therefore, the median is the average of the 40th and 41th observations. That is,
Thus, the median age of the bus is 4.5 years.
The contingency table for the maintenance cost and age of the buses is as follows:
| Maintenance cost | Age | ||
| Below median | Above median | Total | |
| Below median | 29 | 11 | 40 |
| Above median | 13 | 27 | 40 |
| Total | 42 | 38 | 80 |
The null and alternative hypotheses are stated below:
The number of degrees of freedom for a contingency table is obtained as follows:
Therefore, the number of degrees of freedom is 1.
Step-by-step procedure to find the test statistic using the MINITAB software:
- Choose Stat > Tables > Chi-Square Test for Association.
- Choose Summarized data in a two-way table.
- In Columns containing the table, enter the columns of Less than median age, and More than median age.
- Under Labels for the table, in Rows enter Maintenance cost and in the columns enter the Age.
- Click OK.
Output obtained using Minitab is as follows:
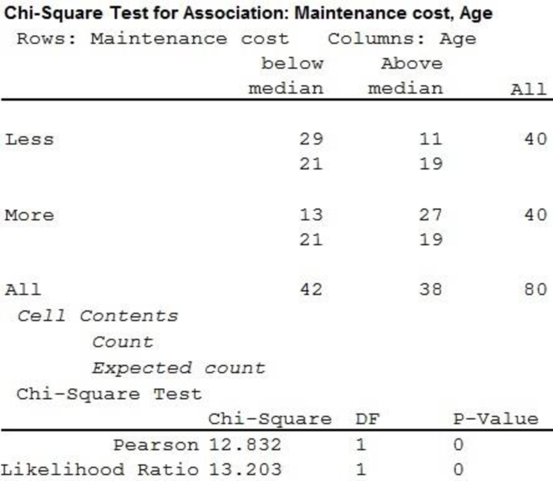
From the above output, the value of the test statistic is 12.832 and the p-value is 0.000.
Conclusion:
The significance level is 0.05 and the p-value is 0.000.
Here, the p-value is less than the significance level 0.05. By the rejection rule, reject the null hypothesis at the 0.05 significance level.
Thus, it can be concluded that the age of the bus is related to the amount of the maintenance cost.
c.
Check whether there is a relationship between the maintenance cost and manufacturer of the bus.
Answer to Problem 64DE
There is a relationship between the maintenance cost and the manufacturer of the bus.
Explanation of Solution
The contingency table for the maintenance cost and manufacturer of the bus is as follows:
| Maintenance cost | Manufacturer | |||
| Bluebird | Keiser | Thompson | Total | |
| Below median | 26 | 14 | 0 | 40 |
| Above median | 21 | 11 | 8 | 40 |
| Total | 47 | 25 | 8 | 80 |
The null and alternative hypotheses are stated below:
The number of degrees of freedom is obtained as follows:
Therefore, the number of degrees of freedom is 1.
Step-by-step procedure to find the test statistic using the MINITAB software:
- Choose Stat > Tables > Chi-Square Test for Association.
- Choose Summarized data in a two-way table.
- In Columns containing the table, enter the columns of below median manufacturer, and above median manufacturer.
- Under Labels for the table, in Rows enter Maintenance cost and in the columns enter the Manufacturer.
- Click OK
Output obtained using Minitab is as follows:
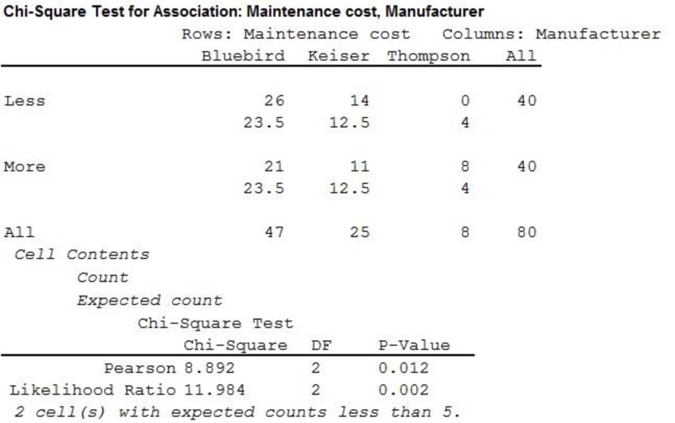
From the above output, the value of the test statistic is 8.892 and the p-value is 0.012.
Conclusion:
The significance level is 0.05 and the p-value is 0.012.
Here, the p-value is less than the significance level 0.05. By the rejection rule, reject the null hypothesis at the 0.05 significance level.
Therefore, there is a relationship between the maintenance cost and the manufacturer.
Want to see more full solutions like this?
Chapter 15 Solutions
Statistical Techniques in Business and Economics
- C4 Q6 V1: Randomly collected student data in the dataset STATISTICSSTUDENTSSURVEYFORR contains the columns FEDBEST (preferred Federal party (Conservative, Green, Liberals, or NDP) ) , UNDERGORGRAD (degree being sought (GraduateProfessional, Undergraduate) ) and GENDERIDENTITY (Female or Male or Other). Make a crosstab (contingency) table of the counts for each of the (UNDERGORGRAD, FEDBEST) pairs for ONLY the females. If we randomly select a female student who is pursuing a graduateprofessional degree, what is the probability that she prefers the Federal Liberals. Choose the most correct (closest) answer below. Question 6 Answer a. 0.128 b. 0.263 c. 0.744 d. 0.333arrow_forwardInstall RStudio: Begin by installing RStudio on your computer. If you haven't done so, please refer to the official RStudio website for download and installation instructions. Watch the Tutorial Video: Watch the provided video tutorial that explains how to run RStudio. Pay close attention to the steps for opening and managing data files. https://www.youtube.com/watch?v=RhJp6vSZ7z0 Open RStudio: Once RStudio is installed, open the application. Load the Dataset: In RStudio, open a data file named "mtcars". To do this, type the command mtcars in the script editor and run the command. Attach the Data: Next, attach the dataset using the command attach(mtcars). Examine the Variables: Carefully review and note the names of all variables in the dataset. Examples of these variables include: Mileage (mpg) Number of Cylinders (cyl) Displacement (disp) Horsepower (hp) Research: Google to understand these variables. Statistical Analysis: Select mpg variable, and perform the following…arrow_forwardA marketing professor has surveyed the students at her university to better understand attitudes towards PPT usage for higher education. To be able to make inferences to the entire student body, the sample drawn needs to represent the university’s student population on all key characteristics. The table below shows the five key student demographic variables. The professor found the breakdown of the overall student body in the university’s fact book posted online. A non-parametric chi-square test was used to test the sample demographics against the population percentages shown in the table above. Review the output for the five chi-square tests on the following pages and answer the five questions: Based on the chi-square test, which sample variables adequately represent the university’s student population and which ones do not? Support your answer by providing the p-value of the chi-square test and explaining what it means. Using the results from Question 1, make recommendation for…arrow_forward
- A marketing professor has surveyed the students at her university to better understand attitudes towards PPT usage for higher education. To be able to make inferences to the entire student body, the sample drawn needs to represent the university’s student population on all key characteristics. The table below shows the five key student demographic variables. The professor found the breakdown of the overall student body in the university’s fact book posted online. A non-parametric chi-square test was used to test the sample demographics against the population percentages shown in the table above. Review the output for the five chi-square tests on the following pages and answer the five questions: Based on the chi-square test, which sample variables adequately represent the university’s student population and which ones do not? Support your answer by providing the p-value of the chi-square test and explaining what it means. Using the results from Question 1, make recommendation for…arrow_forwardA retail chain is interested in determining whether a digital video point-of-purchase (POP) display would stimulate higher sales for a brand advertised compared to the standard cardboard point-of-purchase display. To test this, a one-shot static group design experiment was conducted over a four-week period in 100 different stores. Fifty stores were randomly assigned to the control treatment (standard display) and the other 50 stores were randomly assigned to the experimental treatment (digital display). Compare the sales of the control group (standard POP) to the experimental group (digital POP). What were the average sales for the standard POP display (control group)? What were the sales for the digital display (experimental group)? What is the (mean) difference in sales between the experimental group and control group? List the null hypothesis being tested. Do you reject or retain the null hypothesis based on the results of the independent t-test? Was the difference between the…arrow_forwardWhat were the average sales for the four weeks prior to the experiment? What were the sales during the four weeks when the stores used the digital display? What is the mean difference in sales between the experimental and regular POP time periods? State the null hypothesis being tested by the paired sample t-test. Do you reject or retain the null hypothesis? At a 95% significance level, was the difference significant? Explain why or why not using the results from the paired sample t-test. Should the manager of the retail chain install new digital displays in each store? Justify your answer.arrow_forward
- A retail chain is interested in determining whether a digital video point-of-purchase (POP) display would stimulate higher sales for a brand advertised compared to the standard cardboard point-of-purchase display. To test this, a one-shot static group design experiment was conducted over a four-week period in 100 different stores. Fifty stores were randomly assigned to the control treatment (standard display) and the other 50 stores were randomly assigned to the experimental treatment (digital display). Compare the sales of the control group (standard POP) to the experimental group (digital POP). What were the average sales for the standard POP display (control group)? What were the sales for the digital display (experimental group)? What is the (mean) difference in sales between the experimental group and control group? List the null hypothesis being tested. Do you reject or retain the null hypothesis based on the results of the independent t-test? Was the difference between the…arrow_forwardQuestion 4 An article in Quality Progress (May 2011, pp. 42-48) describes the use of factorial experiments to improve a silver powder production process. This product is used in conductive pastes to manufacture a wide variety of products ranging from silicon wafers to elastic membrane switches. Powder density (g/cm²) and surface area (cm/g) are the two critical characteristics of this product. The experiments involved three factors: reaction temperature, ammonium percentage, stirring rate. Each of these factors had two levels, and the design was replicated twice. The design is shown in Table 3. A222222222222233 Stir Rate (RPM) Ammonium (%) Table 3: Silver Powder Experiment from Exercise 13.23 Temperature (°C) Density Surface Area 100 8 14.68 0.40 100 8 15.18 0.43 30 100 8 15.12 0.42 30 100 17.48 0.41 150 7.54 0.69 150 8 6.66 0.67 30 150 8 12.46 0.52 30 150 8 12.62 0.36 100 40 10.95 0.58 100 40 17.68 0.43 30 100 40 12.65 0.57 30 100 40 15.96 0.54 150 40 8.03 0.68 150 40 8.84 0.75 30 150…arrow_forward- + ++ Table 2: Crack Experiment for Exercise 2 A B C D Treatment Combination (1) Replicate I II 7.037 6.376 14.707 15.219 |++++ 1 བྱ॰༤༠སྦྱོ སྦྱོཋཏྟཱུ a b ab 11.635 12.089 17.273 17.815 с ас 10.403 10.151 4.368 4.098 bc abc 9.360 9.253 13.440 12.923 d 8.561 8.951 ad 16.867 17.052 bd 13.876 13.658 abd 19.824 19.639 cd 11.846 12.337 acd 6.125 5.904 bcd 11.190 10.935 abcd 15.653 15.053 Question 3 Continuation of Exercise 2. One of the variables in the experiment described in Exercise 2, heat treatment method (C), is a categorical variable. Assume that the remaining factors are continuous. (a) Write two regression models for predicting crack length, one for each level of the heat treatment method variable. What differences, if any, do you notice in these two equations? (b) Generate appropriate response surface contour plots for the two regression models in part (a). (c) What set of conditions would you recommend for the factors A, B, and D if you use heat treatment method C = +? (d) Repeat…arrow_forward
- Question 2 A nickel-titanium alloy is used to make components for jet turbine aircraft engines. Cracking is a potentially serious problem in the final part because it can lead to nonrecoverable failure. A test is run at the parts producer to determine the effect of four factors on cracks. The four factors are: pouring temperature (A), titanium content (B), heat treatment method (C), amount of grain refiner used (D). Two replicates of a 24 design are run, and the length of crack (in mm x10-2) induced in a sample coupon subjected to a standard test is measured. The data are shown in Table 2. 1 (a) Estimate the factor effects. Which factor effects appear to be large? (b) Conduct an analysis of variance. Do any of the factors affect cracking? Use a = 0.05. (c) Write down a regression model that can be used to predict crack length as a function of the significant main effects and interactions you have identified in part (b). (d) Analyze the residuals from this experiment. (e) Is there an…arrow_forwardA 24-1 design has been used to investigate the effect of four factors on the resistivity of a silicon wafer. The data from this experiment are shown in Table 4. Table 4: Resistivity Experiment for Exercise 5 Run A B с D Resistivity 1 23 2 3 4 5 6 7 8 9 10 11 12 I+I+I+I+Oooo 0 0 ||++TI++o000 33.2 4.6 31.2 9.6 40.6 162.4 39.4 158.6 63.4 62.6 58.7 0 0 60.9 3 (a) Estimate the factor effects. Plot the effect estimates on a normal probability scale. (b) Identify a tentative model for this process. Fit the model and test for curvature. (c) Plot the residuals from the model in part (b) versus the predicted resistivity. Is there any indication on this plot of model inadequacy? (d) Construct a normal probability plot of the residuals. Is there any reason to doubt the validity of the normality assumption?arrow_forwardStem1: 1,4 Stem 2: 2,4,8 Stem3: 2,4 Stem4: 0,1,6,8 Stem5: 0,1,2,3,9 Stem 6: 2,2 What’s the Min,Q1, Med,Q3,Max?arrow_forward
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL


