
(a)
Using the vertical curvature determine minimum length of vertical curve.
Answer to Problem 4P
Explanation of Solution
Given information:
Station
Elevation
Grades
Grades
Design speed of
Calculation:
Length of curve is given by formula,
A is the grade difference between
Rate of vertical curvature from textbook Table
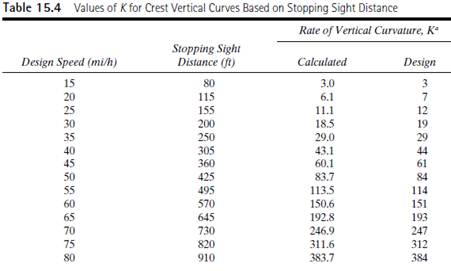
Substitute in equation
Minimum length of vertical curve is
(b)
Stations and elevations of BVC and EVC.
Answer to Problem 4P
Station at BVC is
Tangent elevation at BVC is
Explanation of Solution
Given information:
Station
Elevation
Grades
Grades
Design speed of
Calculation:
Therefore station at BVC is
Therefore tangent elevation at BVC is
(c)
Elevation at each
Answer to Problem 4P
| Station | BVC distance
| Tangent elevation | offset | Curve elevation(Tangent elevation) |
Explanation of Solution
Given information:
Station
Elevation
Grades
Grades
Design speed of
Calculation:
Determine the offset,
For every
| Station | BVC distance
| Tangent elevation | offset | Curve elevation(Tangent elevation) |
(d)
Station and elevation of high point.
Answer to Problem 4P
Explanation of Solution
Given information:
Station
Elevation
Grades
Grades
Design speed of
Calculation:
Distance of the high point of BVC is given by,
Difference beteween both elevation of BVC and highpoint.
Conclusion:
Therefore elevation of high point is
Want to see more full solutions like this?
Chapter 15 Solutions
Traffic and Highway Engineering
- 10.60 As shown, water (15°C) is draining from a tank through a galvanized iron pipe. The pipe length is L = 2 m, the tank depth is H = 1 m, and the pipe is a 0.5-inch NPS schedule 40. Calculate the velocity in the pipe. Neglect component head loss. H Pipe of diameter D L Problems 10.59 and 10.60arrow_forward10.53 Water is pumped through a vertical 10-cm new steel pipe to an elevated tank on the roof of a building. The pressure on the discharge side of the pump is 1.6 MPa. What pressure can be expected at a point in the pipe 110 m above the pump when the flow is 0.02 m³/s? Assume T = 20°C.arrow_forward10.61 A pipeline is to be designed to carry crude oil (SG = 0.93, v = 10-5 m²/s) with a discharge of 0.10 m³/s and a head loss per kilometer of 50 m. What diameter of steel pipe is needed? What power output from a pump is required to maintain this flow? Available pipe diameters are 20, 22, and 24 cm.arrow_forward
- Calculate the active earth pressure (exerted by the supported soil mass on the right) against the 10-meter-long, dense and smooth sheet pile wall shown in Figure E2:1. The ground surface is loaded with heavy construction machinery applying a pressure of q = 10.0 kPa. Other data is according to the figure.Assume the sheet pile moves sufficiently to the left to reach active failure conditions behind it, and passive failure conditions develop in the soil mass below the excavation bottom. Will the sheet pile wall hold without rain? (Calculate the forces.) Will the sheet pile wall hold if it rains? (Assume water-filled cracks.) If the sheet pile does not hold in any of the above cases – how deep would it need to be embedded in order to hold? Draw diagrams for active and passive earth pressure as well as the resultant earth pressure. gvy=grownd water levelarrow_forwardThe composite beam shown in the figure is subjected to a bending moment Mz=8 kNmMz=8kNm.The elastic moduli for the different parts are E1=30 GPa, E2=20 GPa, and E3=60GPa. a) Determine the reduced moment of inertia IredIred for the entire beam. b) Sketch the bending stress distribution in the beam.arrow_forwardUSING THE ATTACHED SKETCH , DETERMINE THE FOLLOWING: 1. INVERSE DISTANCE, NORTH AZIMUTH AND BEARING BETWEEN CP-102 AND THE SOUTHWEST BUILDING CORNER.2. DETERMINE THE INTERIOR ANGLE AT CP-101 - CP-102 AND THE SOUTHWEST BUILDING CORNER.3. WHAT ARE THE COORDINATES (N,E) AT POINT A AND POINT B IN THE ATTACHED SKETCH?arrow_forward
- Given the following Right Triangle, find the " Area by Coordinates" (Not B*H/2). Report to the nearest Sq. Ft. and to the nearest thousandth of an acre.arrow_forward1) 4,739,281 SQ.FT. = ______________________ ACRES? 2) S 90°00'00" W IS ALSO KNOW AS WHAT CARDINAL DIRECTION? 3) CALCULATE THE NORTH AZIMUTH (NAZ) OF THE FOLLOWING BEARINGS: N 31° 22' 22" E=___________________________NAZ? S 87° 29' 17" W=___________________________NAZ? S 27° 43' 27" E=___________________________NAZ? N 43° 17' 43" E=___________________________NAZ?arrow_forward1) 187.25597°=_____________________________________(DEG-MIN-SEC FORMAT)? 2) CALCULATE THE BEARING AND DIRECTION IN DEG-MIN-SEC OF THE FOLLOWING: NAZ 142°49'18"=____________________________(BEARING/DIRECTION DEG-MIN-SEC)? NAZ 180°00'00"=____________________________(BEARING/DIRECTION DEG-MIN-SEC)? NAZ 270°00'00"=____________________________(BEARING/DIRECTION DEG-MIN-SEC)?arrow_forward
- A traffic signal has a 60-second cycle length (Red time + Green time). For the travel direction of interest, the red and green times are 30 seconds each, the arrival rate is constant at 20 [veh/min] and the saturation flow (i.e., the departure rate) is 1 [veh/sec]. a. Calculate the average delay (for all vehicles) for the travel direction of interest. b. Assume a work zone on the street downstream of the intersection so that only 25 [veh/min] (in the direction of interest) can pass. Calculate the average delay caused by the work zone to a vehicle leaving the intersection. Assume that the queue at the work zone never backs- up into the intersection. c. Discuss qualitatively the implications of queue spillback from the work zone on the delay of the system. Traffic Direction (a) Traffic Direction (b)arrow_forwardCalculate the active earth pressure (exerted by the supported soil mass on the right) against the 10-meter-long, dense and smooth sheet pile wall shown in Figure E2:1. The ground surface is loaded with heavy construction machinery applying a pressure of q = 10.0 kPa. Other data is according to the figure.Assume the sheet pile moves sufficiently to the left to reach active failure conditions behind it, and passive failure conditions develop in the soil mass below the excavation bottom. Draw diagrams for active and passive earth pressure as well as the resultant earth pressure. Questions to Answer: Will the sheet pile wall hold without rain? (Calculate the forces.) Will the sheet pile wall hold if it rains? (Assume water-filled cracks.) If the sheet pile does not hold in any of the above cases – how deep would it need to be embedded in order to hold?arrow_forwardQ.2- Design a flexible pavement by AASHTO method and draw typical cross section of the flexible Pavement for rural highway has following data: - Elastic modulus of Asphalt is 450000 Ib/in², Mr. of base-31000 psi, Mr. of subbase=13500 psi, CBR of base-100 CBR of subbase=22 subbase of subgrade =6 water removed with one week Percentage of time pavement structure is exposed to moisture levels-30% reliability=95% Standard deviation=0.45 initial serviceability=4.2 terminal serviceability=2.5 and ESAL=2*106 subgrade =1500 CBR Mr كلية . المنصور الجامعةarrow_forward
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
