Student Workbook for Physics for Scientists and Engineers: A Strategic Approach, Vol 1. (Chs 1-21)
4th Edition
ISBN: 9780134110646
Author: Randall D. Knight (Professor Emeritus)
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 15, Problem 3CQ
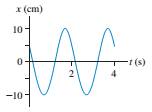
FIGURE Q15.3 shows a position-versus-time graph for a particle in
FIGURE Q15.3
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 15 Solutions
Student Workbook for Physics for Scientists and Engineers: A Strategic Approach, Vol 1. (Chs 1-21)
Ch. 15 - Prob. 1CQCh. 15 - A pendulum on Planet X, where the value of g is...Ch. 15 - FIGURE Q15.3 shows a position-versus-time graph...Ch. 15 - FIGURE Q15.4 shows a position-versus-time graph...Ch. 15 - 5. Equation 15.25 states that . What does this...Ch. 15 - A block oscillating on a spring has an amplitude...Ch. 15 - A block oscillating on a spring has a maximum...Ch. 15 - 8. The solid disk and circular hoop in FIGURE...Ch. 15 - FIGURE Q15.9 shows the potential-energy diagram...Ch. 15 - Suppose the damping constant b of an oscillator...
Ch. 15 - Prob. 11CQCh. 15 - 12. What is the difference between the driving...Ch. 15 - An air-track glider attached to a spring...Ch. 15 - An air-track is attached to a spring. The glider...Ch. 15 - Prob. 3EAPCh. 15 - An object in SHM oscillates with a period of 4.0 s...Ch. 15 - What are the (a) amplitude, (b) frequency, and (c)...Ch. 15 - What are the (a) amplitude, (b) frequency, and (c)...Ch. 15 - FIGURE EX15.7 is the Position-versus-time graph of...Ch. 15 - FIGURE EX15.8 is the velocity-versus-time graph of...Ch. 15 - An object in simple harmonic motion has an...Ch. 15 - An object in simple harmonic motion has amplitude...Ch. 15 - An object in simple harmonic motion has amplitude...Ch. 15 - An object in simple harmonic motion has amplitude...Ch. 15 - An air-track glider attached to a spring...Ch. 15 - 14. A block attached to a spring with unknown...Ch. 15 - 15. A 200 g air-track glider is attached to a...Ch. 15 - A 200 g mass attached to a horizontal spring...Ch. 15 - Prob. 17EAPCh. 15 - A 1.0 kg block is attached to a spring with spring...Ch. 15 - Prob. 19EAPCh. 15 - Prob. 20EAPCh. 15 - A spring is hanging from the ceiling. Attaching a...Ch. 15 - 22. A spring with spring constant 15 N/m hangs...Ch. 15 - 23. A spring is hung from the ceiling. When a...Ch. 15 - Prob. 24EAPCh. 15 - A 200 g ball is tied to a string. It is pulled to...Ch. 15 - Prob. 26EAPCh. 15 - Prob. 27EAPCh. 15 - Prob. 28EAPCh. 15 - Prob. 29EAPCh. 15 - A 100 g mass on a 1.0-m-long string is pulled 8.0...Ch. 15 - A uniform steel bar swings from a pivot at one end...Ch. 15 - Prob. 32EAPCh. 15 - Prob. 33EAPCh. 15 - Prob. 34EAPCh. 15 - Vision is blurred if the head is vibrated at 29 Hz...Ch. 15 - Prob. 36EAPCh. 15 - Prob. 37EAPCh. 15 - a. When the displacement of a mass on a spring is...Ch. 15 - For a particle in simple harmonic motion, show...Ch. 15 - A 100g block attached to a spring with spring...Ch. 15 - A 0.300 kg oscillator has a speed of 95.4cm/s when...Ch. 15 - An ultrasonic transducer, of the type used in...Ch. 15 - Astronauts in space cannot weigh themselves by...Ch. 15 - 44. Your lab instructor has asked you to measure a...Ch. 15 - A 5.0 kg block hangs from a spring with spring...Ch. 15 - Prob. 46EAPCh. 15 - A block hangs in equilibrium from a vertical...Ch. 15 - Prob. 48EAPCh. 15 -
49. Scientists are measuring the properties of a...Ch. 15 - Prob. 50EAPCh. 15 - A compact car has a mass of 1200 kg. Assume that...Ch. 15 - Prob. 52EAPCh. 15 - Prob. 53EAPCh. 15 - Prob. 54EAPCh. 15 - Prob. 55EAPCh. 15 - Prob. 56EAPCh. 15 - Prob. 57EAPCh. 15 - A uniform rod of mass M and length L swings as a...Ch. 15 - Prob. 59EAPCh. 15 - 60. A 500 g air-track glider attached to a spring...Ch. 15 - Prob. 61EAPCh. 15 - Prob. 62EAPCh. 15 - A molecular bond can be modeled as a spring...Ch. 15 - Prob. 64EAPCh. 15 - Prob. 65EAPCh. 15 - Prob. 66EAPCh. 15 - The 15 g head of a bobble-head doll oscillates in...Ch. 15 - An oscillator with a mass of 500 g and a period of...Ch. 15 - Prob. 69EAPCh. 15 - Prob. 70EAPCh. 15 - Prob. 71EAPCh. 15 - Prob. 72EAPCh. 15 - Prob. 73EAPCh. 15 - A block ona frictionless FIGURE P15.74 to two...Ch. 15 - Prob. 75EAPCh. 15 - Prob. 76EAPCh. 15 - A solid sphere of mass M and radius R is suspended...Ch. 15 - A uniform rod of length L oscillates as a pendulum...Ch. 15 - Prob. 79EAPCh. 15 - Prob. 80EAPCh. 15 - FIGURE CP15.81 shows a 200 g uniform rod pio4ed at...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A block of mass m rests on a frictionless, horizontal surface and is attached to two springs with spring constants k1 and k2 (Fig. P16.22). It is displaced to the right and released. Find an expression for the angular frequency of oscillation of the resulting simple harmonic motion. FIGURE P16.22 Problems 22 and 81.arrow_forwardA spherical bob of mass m and radius R is suspended from a fixed point by a rigid rod of negligible mass whose length from the point of support to the center of the bob is L (Fig. P16.75). Find the period of small oscillation. N The frequency of a physical pendulum comprising a nonuniform rod of mass 1.25 kg pivoted at one end is observed to be 0.667 Hz. The center of mass of the rod is 40.0 cm below the pivot point. What is the rotational inertia of the pendulum around its pivot point?arrow_forward(a) If frequency is not constant for some oscillation, can the oscillation be SHM? (b) Can you think of any examples of harmonic motion where the frequency may depend on the amplitude?arrow_forward
- Review. A system consists of a spring with force constant k = 1 250 N/m, length L = 1.50 m, and an object of mass m = 5.00 kg attached to the end (Fig. P15.49). The object is placed at the level of the point of attachment with the spring unstretched, at position yi = L, and then it is released so that it swings like a pendulum. (a) Find the y position of the object at the lowest point. (b) Will the pendulums period be greater or less than the period of a simple pendulum with the same mass m and length L? Explain. Figure PI 5.49arrow_forwardA spring of negligible mass stretches 3.00 cm from its relaxed length when a force of 7.50 N is applied. A 0.500-kg particle rests on a frictionless horizontal surface and is attached to the free end of the spring. The particle is displaced from the origin to x = 5.00 cm and released from rest at t = 0. (a) What is the force constant of the spring? (b) What are the angular frequency , the frequency, and the period of the motion? (c) What is the total energy of the system? (d) What is the amplitude of the motion? (c) What are the maximum velocity and the maximum acceleration of the particle? (f) Determine the displacement x of the particle from the equilibrium position at t = 0.500 s. (g) Determine the velocity and acceleration of the particle when t = 0.500 s.arrow_forwardDetermine the angular frequency of oscillation of a thin, uniform, vertical rod of mass m and length L pivoted at the point O and connected to two springs (Fig. P16.78). The combined spring constant of the springs is k(k = k1 + k2), and the masses of the springs are negligible. Use the small-angle approximation (sin ). FIGURE P16.78arrow_forward
- An object of mass m1 = 9.00 kg is in equilibrium when connected to a light spring of constant k = 100 N/m that is fastened to a wall as shown in Figure P12.67a. A second object, m2 = 7.00 kg, is slowly pushed up against m1, compressing the spring by the amount A = 0.200 m (see Fig. P12.67b). The system is then released, and both objects start moving to the right on the frictionless surface. (a) When m1 reaches the equilibrium point, m2 loses contact with m1 (see Fig. P12.67c) and moves to the right with speed v. Determine the value of v. (b) How far apart are the objects when the spring is fully stretched for the first time (the distance D in Fig. P12.67d)? Figure P12.67arrow_forwardA small ball of mass M is attached to the end of a uniform rod of equal mass M and length L that is pivoted at the top (Fig. P12.59). Determine the tensions in the rod (a) at the pivot and (b) at the point P when the system is stationary. (c) Calculate the period of oscillation for small displacements from equilibrium and (d) determine this period for L = 2.00 m. Figure P12.59arrow_forwardA Two springs, with spring constants k1 and k2, are connected to a block of mass m on a frictionless, horizontal table (Fig. P16.80). The block is extended a distance x from equilibrium and released from rest. Show that the block executes simple harmonic motion with a period given by T=2m(k1+k2)k1k2 FIGURE P16.80arrow_forward
- We do not need the analogy in Equation 16.30 to write expressions for the translational displacement of a pendulum bob along the circular arc s(t), translational speed v(t), and translational acceleration a(t). Show that they are given by s(t) = smax cos (smpt + ) v(t) = vmax sin (smpt + ) a(t) = amax cos(smpt + ) respectively, where smax = max with being the length of the pendulum, vmax = smax smp, and amax = smax smp2.arrow_forwardConsider the simplified single-piston engine in Figure CQ12.13. Assuming the wheel rotates with constant angular speed, explain why the piston rod oscillates in simple harmonic motion. Figure CQ12.13arrow_forwardWhich of the following statements is not true regarding a massspring system that moves with simple harmonic motion in the absence of friction? (a) The total energy of the system remains constant. (b) The energy of the system is continually transformed between kinetic and potential energy. (c) The total energy of the system is proportional to the square of the amplitude. (d) The potential energy stored in the system is greatest when the mass passes through the equilibrium position. (e) The velocity of the oscillating mass has its maximum value when the mass passes through the equilibrium position.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY