
Concept explainers
Find the member end moments and reaction for the frames.
Answer to Problem 31P
The end moments at the member AC
Explanation of Solution
Calculation:
Consider the elastic modulus E of the frame is constant.
Show the free body diagram of the entire frame as in Figure 1.
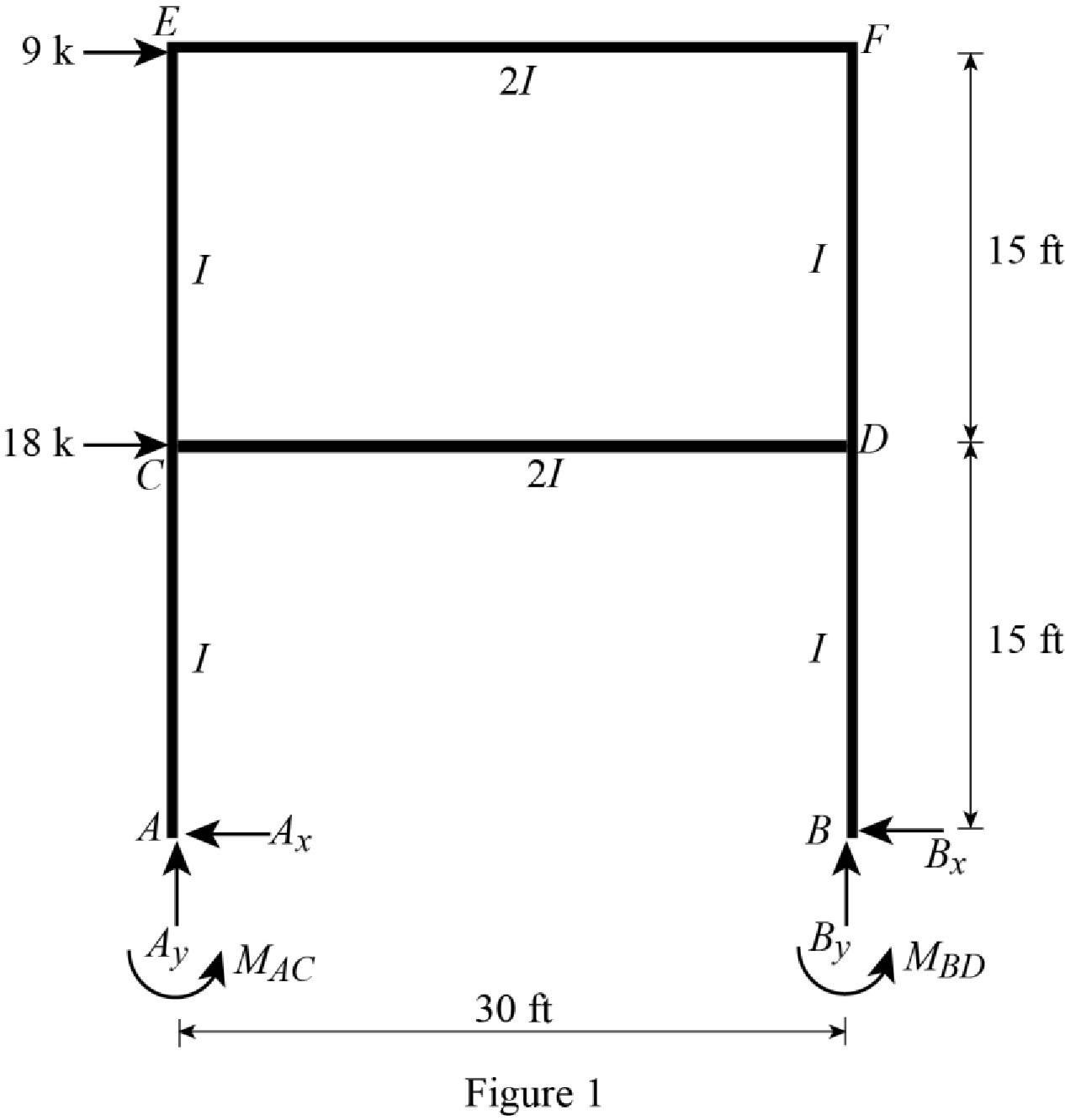
Refer Figure 1,
Calculate the fixed end moment for AC.
Calculate the fixed end moment for CA.
Calculate the fixed end moment for CD.
Calculate the fixed end moment for DC.
Calculate the fixed end moment for DB.
Calculate the fixed end moment for BD.
Calculate the fixed end moment for CE.
Calculate the fixed end moment for EC.
Calculate the fixed end moment for EF.
Calculate the fixed end moment for FE.
Calculate the fixed end moment for FD.
Calculate the fixed end moment for DF.
Chord rotations:
Show the free body diagram of the chord rotation of the frame as in Figure 2.
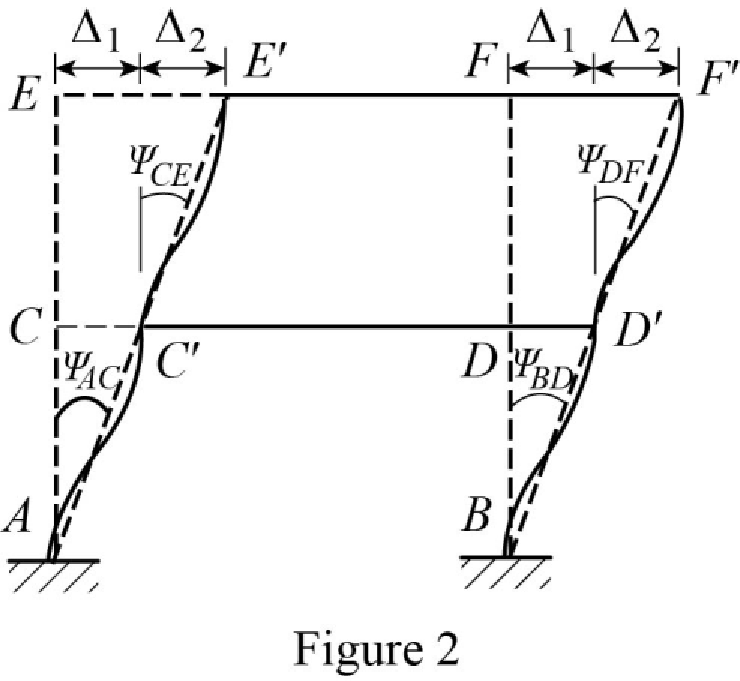
Refer Figure 2,
Calculate the chord rotation of the frame AC and BD.
Calculate the chord rotation of the frame CE and DF.
Calculate the chord rotation of the frame CD and EF.
Calculate the slope deflection equation for the member AC.
Substitute 15 ft for L, 0 for
Calculate the slope deflection equation for the member CA.
Substitute 15 ft for L, 0 for
Calculate the slope deflection equation for the member CD.
Substitute 30 ft for L, 0 for
Calculate the slope deflection equation for the member DC.
Substitute 30 ft for L, 0 for
Calculate the slope deflection equation for the member DB.
Substitute 15 ft for L, 0 for
Calculate the slope deflection equation for the member BD.
Substitute 15 ft for L, 0 for
Calculate the slope deflection equation for the member CE.
Substitute 15 ft for L,
Calculate the slope deflection equation for the member EC.
Substitute 15 ft for L,
Calculate the slope deflection equation for the member EF.
Substitute 30 ft for L, 0 for
Calculate the slope deflection equation for the member FE.
Substitute 30 ft for L, 0 for
Calculate the slope deflection equation for the member FD.
Substitute 15 ft for L,
Calculate the slope deflection equation for the member DF.
Substitute 15 ft for L,
Write the equilibrium equation as below.
Substitute equation (2), equation (3), and equation (7) in above equation.
Write the equilibrium equation as below.
Substitute equation (4), equation (5) and equation (12) in above equation.
Write the equilibrium equation as below.
Substitute equation (8) and equation (9) in above equation.
Write the equilibrium equation as below.
Substitute equation (10) and equation (11) in above equation.
Show the free body diagram of the joint E and F due to sway force as in Figure 3.
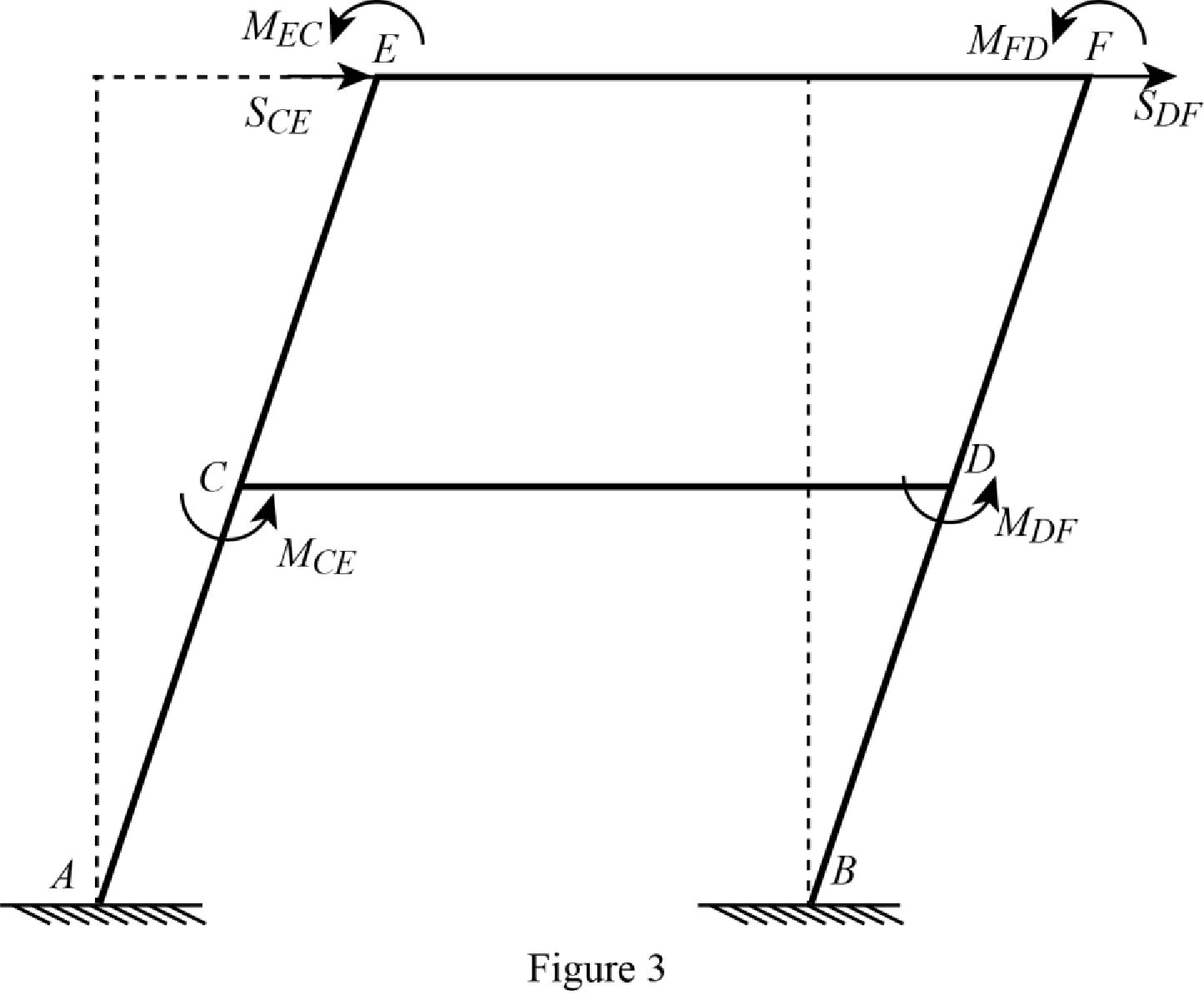
Calculate the horizontal reaction at the member CE due to sway force by taking moment about point C.
Calculate the horizontal reaction at the member DF due to sway force by taking moment about point D.
Calculate the reaction of the support E and support F due to sway force by considering horizontal equilibrium.
Substitute equation (7), (8), (11) and (12).
Show the free body diagram of the joint C and D due to sway force as in Figure 4.
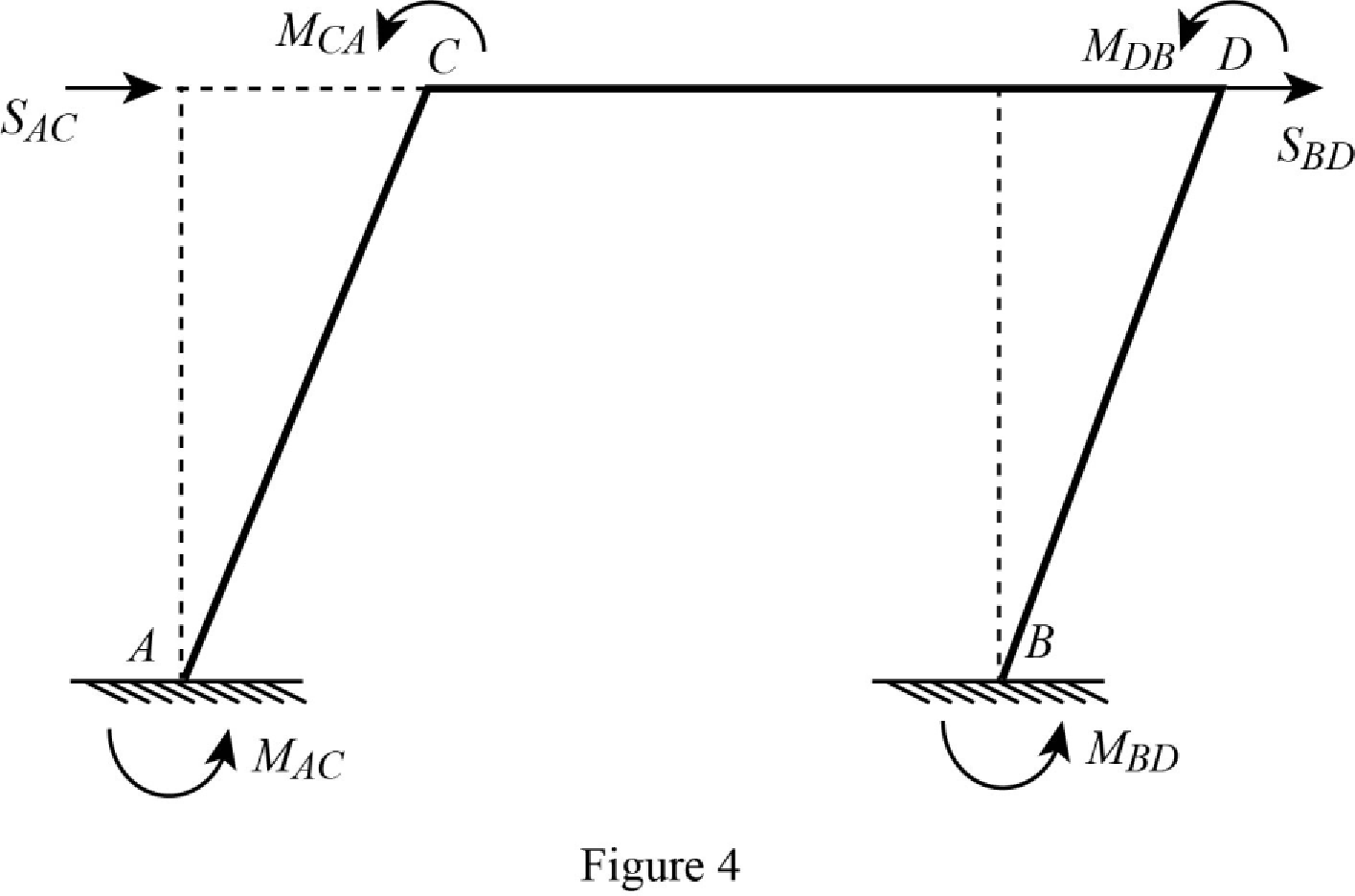
Calculate the horizontal reaction at the member AC due to sway force by taking moment about point A.
Calculate the horizontal reaction at the member BD due to sway force by taking moment about point B.
Calculate the reaction of the support C and support D due to sway force by considering horizontal equilibrium.
Substitute equation (1), equation (2), equation (5), and equation (6).
Solve the equation (13), equation (14), equation (15), equation (16), equation (17) and equation (18).
Calculate the moment about AC.
Substitute
Calculate the moment about CA.
Substitute
Calculate the moment about CD.
Substitute
Calculate the moment about DC.
Substitute
Calculate the moment about DB.
Substitute
Calculate the moment about BD.
Substitute
Calculate the moment about CE.
Substitute
Calculate the moment about EC.
Substitute
Calculate the moment about EF.
Substitute
Calculate the moment about FE.
Substitute
Calculate the moment about FD.
Substitute
Calculate the moment about DF.
Substitute
Show the section free body diagram of the member EF as in Figure 5.
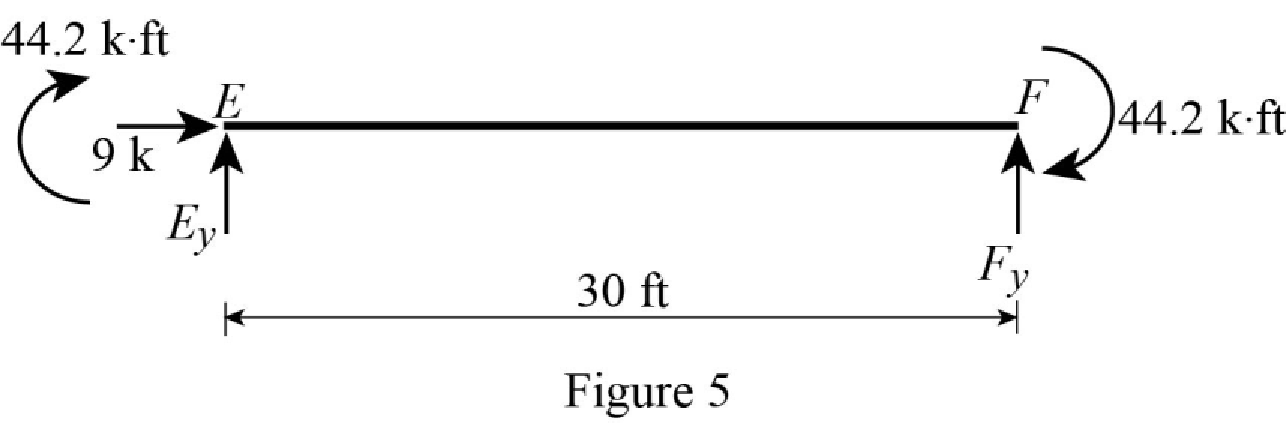
Consider member EF:
Calculate the vertical reaction at the joint E by taking moment about point F.
Calculate the vertical reaction at joint F by resolving the horizontal equilibrium.
Show the section free body diagram of the member CD as in Figure 6.
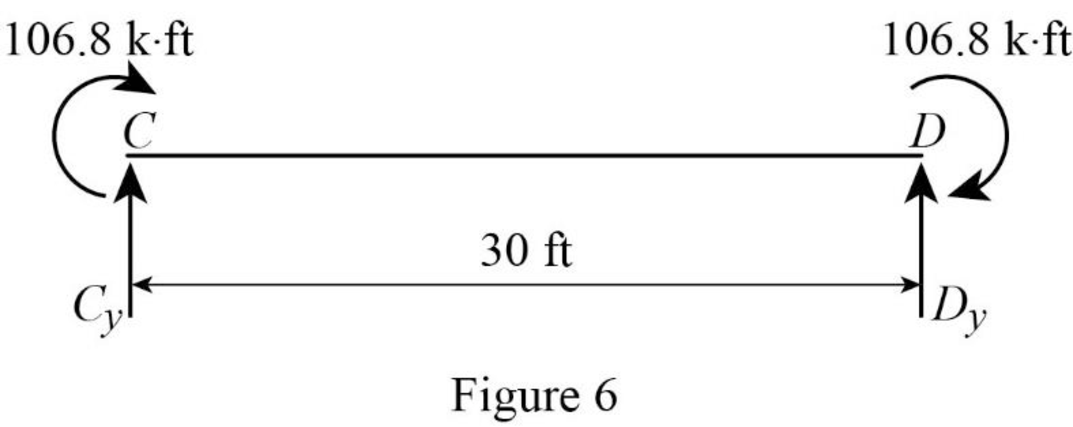
Consider member CD:
Calculate the vertical reaction at the joint C by taking moment about point D.
Calculate the vertical reaction at joint D by resolving the horizontal equilibrium.
Show the section free body diagram of the member AC, CE, DB and FD as in Figure 7.
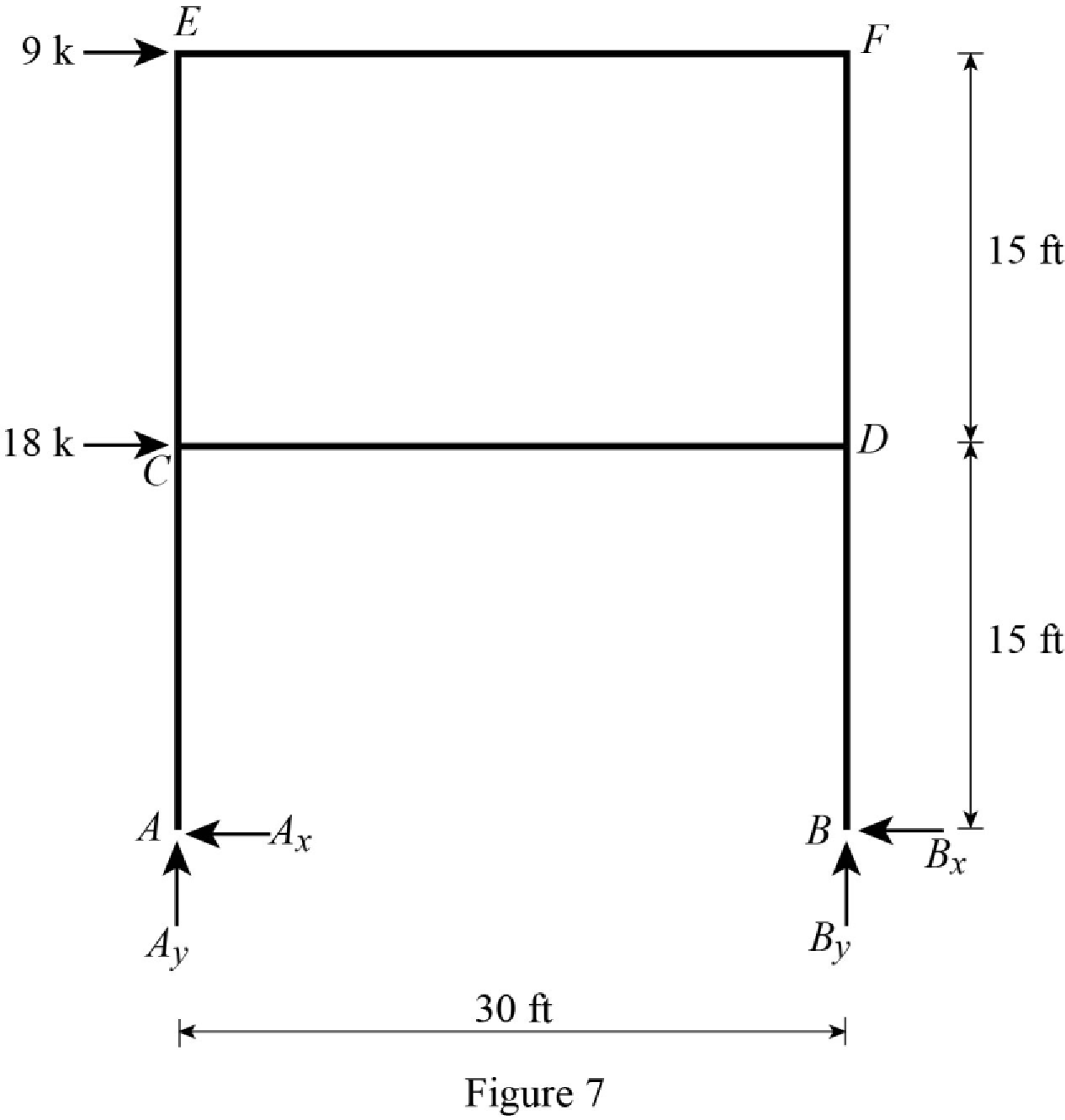
Calculate the reaction at joint A:
Calculate the reaction at joint B:
Consider member AC:
Calculate the horizontal reaction at the joint A by taking moment about point C.
Consider member BD:
Calculate the horizontal reaction at the joint B by taking moment about point D.
Show the reactions of the frame as in Figure 8.

Want to see more full solutions like this?
Chapter 15 Solutions
Structural Analysis, Si Edition
- Water is discharged into the atmosphere through a bent nozzle of an angle (a) as shown in the figure. The cross-sectional area at the nozzle inlet and outlet are (Ain) and (Aout), respectively. The discharge through the nozzle is (Q). The gauge pressure at the nozzle inlet is (Pin). The bend lies in a horizontal plane. Ain Vin Aout X Atmosphere Vout Problem (10): Given the values of Ain [m2], Aout [m²], Pin [atm], Q [m³/s], and a [degrees], calculate the magnitude of the reaction force component in y-direction (Ry) in [N]. Givens: A in 0.169 m^2 A out Pin 0.143 m^2 0.552 atm = Q α 0.367 m^3/s = 31.72 degrees Answers: ( 1 ) 6264.193 N (2) 12041.886 N ( 3 ) 8715.747 N ( 4 ) 7139.937 Narrow_forwardProblem (12): A pump is being used to lift water from the bottom tank to the top tank in a pipe of diameter (d) at a discharge (Q). The pipe system comprises four Long radius 90° threaded elbows. The pipe entrance is sharp-edged, and the pipe exit is sudden. A Ball valve (1/3 closed) is used to control the discharge in the pipeline. Given the values of Q [Lit/s], and d [cm], calculate the power loss due to components (i.e., minor losses) in the pipe (Wminor-loss) in [W]. Givens: Q = 12.275 lit/s d = 6.266 cm Answers: ( 1 ) 1142.006 W (2) 952.086 W ( 3 ) 1225.555 W ( 4 ) 1331.216 W Loss Coefficients for Pipe Components (h,= K,Y) Component a. Elbows KL elbow Regular 90°, flanged 0.3 Regular 90°, threaded 1.5 Long radius 90°, flanged 0.2 V 90° elbow Long radius 90°, threaded 0.7 Long radius 45°, flanged 0.2 0.4 Regular 45°, threaded . 180° return bends 180° return bend, flanged 0.2 V 45° elbow 180° return bend, threaded 1.5 c. Tees Line flow, flanged 0.2 Line flow, threaded 0.9 180°…arrow_forwardCompute for the stresses (initial, const and final stage) and check for compliance in NSCP provisions. Also compute the following: 1. Compute and check if the section is Uncracked, Transition or Cracked as per NSCP. 2. Compute for its flexural capacity and check if it could carry the given load. BEAM SECTION NOT TO SCALE 1400mm 300 $1098 400 */ 400*300* 300 200 300 100 ORIGINAL SECTION/PRECA CAST-IN-PLACE (CIP) PART PRECAST LOADING AT SERVICE M • 21 KN (DEAD LOAD ONLY) 21KN 4.75m 9.25m CIVEN DATA STRANDS: 12-02 AT 120KN/STRAND (GOMM FROM BOTTOM) 8-2 AT 120HN/STRAND (120mm FROM BOTTOM) fc 42.5 MPa (BEAM) fc 38 MPa (CIP) f'a = 80% or fa fp-1860 MPa ESTRANDS 1976Pa OONG 23.6/m³ LOES 1-8% Loss 18% APPLY 3M LIVE LOAD AT CONST. PHASEarrow_forward
- 4. Determine the stability of the cantilever shown in the figure below (use Coulomb earth theory for the lateral stress due to the backfill material). 1 m 0.5 m Backfill 7 = 18.5 kN/m³ • = 30° 20 6 = 20° 6 m Y₁ = 24 kN/m³ 1.2 m 1 m 4.5 m Base soil Clay: 7 = 19 kN/m³,0 = 30%, 0,, = 20°, s,, = 94 kPa a. With s₁ = c = 94 kPa (disregard values), determine allowable soil bearing capacity of the base soil if the factor of safety is equal to 3. b. Determine the FS against overturning. C. Determine the FS against sliding if the coefficient of friction between footing concrete base and soil is b. d. Determine the FS for bearing capacity.arrow_forwardDirections: Show your solutions explicitly, i.e., do not just write the final answer. 1. A wall footing is to be constructed on a clay soil 1.4 below the ground. The footing is to support a wall that imposes a load of 130 kN per meter of wall length. Considering general shear failure, determine the following: 130 kN/mm 1.4 m a. Footing width if the factor of safety is 3. b. Ultimate bearing capacity if B = 0.95 m. C. New factor of safety. y = 17.92 kN/m² c = 14.5 kPa $ = 30° 1.5 m and has its hottom 2 m below the ground surface.arrow_forward2. A square footing shown has a dimension of 1.5 m x 1.5 m and has its bottom 2 m below the ground surface. The groundwater table is located at a depth of 3 m below the ground surface. Assume a general shear failure. Determine the following: 2 m y = 16 kN/m³ c = 14.5 kPa → = 28° 3 m 1,5 m ysat 18.5 kN/m³ a. Ultimate bearing capacity of the soil beneath the footing (in kPa). b. Allowable bearing capacity if it has a factor of safety of 3 (in kPa). C. Allowable load that the footing could carry (in kN). d. Allowable net bearing capacity if factor of safety is 3. Allowable net load if factor of safety is 3.arrow_forward
- Problem (11): A pipe discharges an unknown fluid into the atmosphere from a tank of depth (h) through a pipe of length (L), and diameter (d). Given the values of L [m], d [cm], and (h) [cm], calculate the discharge rate (Q) [lit/s] that would maintain Laminar flow in the pipe with a Reynolds number of Re-1500. Ignore minor losses. Givens: L = 139.364 m d = 12.614 cm h = 76.609 cm Answers: ( 1 ) 6.911 lit/s (2) 8.179 lit/s ( 3 ) 4.244 lit/s (4) 4.987 lit/s h darrow_forwardB2. For the truss below, determine all member forces. Hint: see the provided slide with the problem set. P₁ = 12 kip and P2 = 6 kip (20 pts). P₁ A 16 ft D 8 ft 8 ft 8 ft B J K E 8 ft 8 ft I H G 8 ft 8 ft 8 ft B₁₂ F ΠΟΙΟΣarrow_forwardDirections: Show your solutions explicitly, I.e., do not just write the final answer. Always simplify and box your final answer. 1. A wall footing is to be constructed on a clay soll 1.4 below the ground. The footing is to support a wall that imposes a load of 130 kN per meter of wall length. Considering general shear failure, determine the following: 130 kN/m 4m a. Footing width if the factor of safety is 3. b. Ultimate bearing capacity if B = 0.95 m. c. New factor of safety. Y = 17.92 kN/m² c = 14.5 kPa $ -30° 2. A square footing shown has a dimension of 1.5 mx 1.5 m and has its bottom 2 m below the ground surface. The groundwater table is located at a depth of 3 m below the ground surface. Assume a general shear failure. Determine the following: L 2 m y = 16 kN/m³ c = 14.5 kPa = 28° 3 m 1.5 m Ysa1 = 18.5 kN/m³ a. Ultimate bearing capacity of the soll beneath the footing (in kPa). b. Allowable bearing capacity if it has a factor of safety of 3 (in kPa). C. Allowable load that the…arrow_forward
- B2. For the truss below, determine all member forces. Hint: see the provided slide with the problem set. P₁ = 12 kip and P₂ = 6 kip (20 pts). P₁ 16 ft D 8 ft 8 ft 8 ft B K E 8 ft 8 ft 8 ft H 8 ft В G 1000 8 ftarrow_forward14.1 A beam of rectangular cross section is 125 mm wide and 200 mm deep. If the maximum bending moment is 28.5 kN⚫m, determine (a) the maximum tensile and compressive bending stress, and (b) the bending stress 25 mm from the top of the section. 14.2 A rectangular beam 50 mm wide and 100 mm deep is subjected to bending. What bending moment will cause a maximum bending stress of 137.9 MN/m² (MPa)? 14.3 Determine the bending moment in a rectangular beam 3 in. wide and 6 in. deep if the maximum bend- ing stress is 15,000 psi.arrow_forwardB3. For the Howe truss below, assume all members are pin connected and take P₁ = 5 kN and P₂ = 10 kN: a. Determine all member forces (16 pts). b. Use a section cut to verify your answers for members GF, GD, and CD (4 Pts) P₁ A H 500 8 0000 B 0000] 2 m m 2 m 3 m B E D marrow_forward
