
State the null and alternative hypothesis.
Find the degrees of freedom for the
Find the critical value of chi-square from Appendix E or from Excel’s
Calculate the chi-square test statistics at 0.05 level of significance.
Interpret the p-value.
Check whether the conclusion is sensitive to the level of significance chosen, identify the cells that contribute to the chi-square test statistic and check for the small expected frequencies.
Perform a two-tailed, two-sample z test for
Answer to Problem 30CE
The null hypothesis is:
And the alternative hypothesis is:
The degrees of freedom for the contingency table is 1.
The critical-value using EXCEL is 3.841.
The chi-square test statistics at 0.05 level of significance is 1.50.
The p-value for the hypothesis test is 0.221.
There is enough evidence to conclude that the correct response and type of cola are independent.
The conclusion is not sensitive to the level of significance chosen.
The cells (1, 1) and (1, 2) contribute the most to the chi-square test statistic.
There is no expected frequencies that are too small.
It is verified that
Explanation of Solution
The table summarizes the grade and order of papers handed in.
The claim is to test whether the data provide sufficient evidence to conclude that the grade and order handed in are independent. If the claim is rejected, then the grade and order handed in are not independent.
The test hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
The degrees of freedom can be obtained as follows:
Substitute 2 for r and 2 for c.
Thus, the degrees of freedom for the contingency table is 1.
Procedure for critical-value using EXCEL:
Step-by-step software procedure to obtain critical-value using EXCEL software is as follows:
- Open an EXCEL file.
- In cell A1, enter the formula “=CHISQ.INV.RT(0.05,1)”
- Output using EXCEL software is given below:
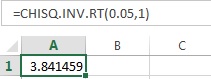
Thus, the critical-value using EXCEL is 3.841.
Test statistic:
Software procedure:
Step by step procedure to obtain the chi-square test statistics and p-value using the MINITAB software:
- Choose Stat > Tables >Cross Tabulation and Chi-Square.
- Choose Row data (categorical variables).
- In Rows, choose Grade.
- In Columns, choose Order handed in.
- In Frequencies, choose Count.
- In Display, select Counts.
- In chi-square, select Chi-square test, Expected cell counts and Each cell’s contribution to chi-square.
- Click OK.
Output using the MINITAB software is given below:
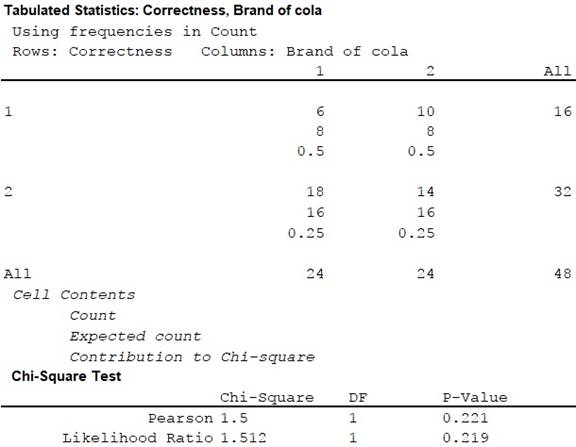
Thus, the test statistic is 1.50 and the p-value for the hypothesis test is 0.221.
Rejection rule:
If the p-value is less than or equal to the significance level, then reject the null hypothesis
Conclusion:
Here, the p-value is greater than the level of significance.
That is,
Therefore, the null hypothesis is not rejected.
Thus, the data provide sufficient evidence to conclude that the correct response and type of cola are independent.
Take
Here, the p-value is greater than the level of significance.
That is,
Therefore, the null hypothesis is not rejected.
Thus, the data provide sufficient evidence to conclude that the correct response and type of cola are independent.
Thus, the conclusion is same for both the significance levels.
Hence, the conclusion is not sensitive to the level of significance chosen.
The cells (1, 1) and (1, 2) contribute the most to the chi-square test statistic.
Since all
Two-tailed, two-sample z test:
The test hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
The proportion of “yes” responses to the regular cola is denoted as
Where
The proportion of number of “yes” responses to the diet cola is denoted as
Where
The pooled proportion is denoted as
Test statistic:
The z-test statistics can be obtained as follows:
Thus, the z-test statistic is –1.22.
The square of the z-test statistic is,
Thus the square of the z-test statistic is same as the chi-square statistics.
Procedure for p-value using EXCEL:
Step-by-step software procedure to obtain p-value using EXCEL software is as follows:
- Open an EXCEL file.
- In cell A1, enter the formula “=2*(1-NORM.S.DIST(–1.22,1))”
- Output using EXCEL software is given below:

Thus, the p-value using EXCEL is 1.778, which is not same as the p-value obtained in chi-square test. But the square of the z-test statistic is same as the chi-square statistics.
Thus, it is verified that
Want to see more full solutions like this?
Chapter 15 Solutions
Applied Statistics in Business and Economics
- For a binary asymmetric channel with Py|X(0|1) = 0.1 and Py|X(1|0) = 0.2; PX(0) = 0.4 isthe probability of a bit of “0” being transmitted. X is the transmitted digit, and Y is the received digit.a. Find the values of Py(0) and Py(1).b. What is the probability that only 0s will be received for a sequence of 10 digits transmitted?c. What is the probability that 8 1s and 2 0s will be received for the same sequence of 10 digits?d. What is the probability that at least 5 0s will be received for the same sequence of 10 digits?arrow_forwardV2 360 Step down + I₁ = I2 10KVA 120V 10KVA 1₂ = 360-120 or 2nd Ratio's V₂ m 120 Ratio= 360 √2 H I2 I, + I2 120arrow_forwardQ2. [20 points] An amplitude X of a Gaussian signal x(t) has a mean value of 2 and an RMS value of √(10), i.e. square root of 10. Determine the PDF of x(t).arrow_forward
- In a network with 12 links, one of the links has failed. The failed link is randomlylocated. An electrical engineer tests the links one by one until the failed link is found.a. What is the probability that the engineer will find the failed link in the first test?b. What is the probability that the engineer will find the failed link in five tests?Note: You should assume that for Part b, the five tests are done consecutively.arrow_forwardProblem 3. Pricing a multi-stock option the Margrabe formula The purpose of this problem is to price a swap option in a 2-stock model, similarly as what we did in the example in the lectures. We consider a two-dimensional Brownian motion given by W₁ = (W(¹), W(2)) on a probability space (Q, F,P). Two stock prices are modeled by the following equations: dX = dY₁ = X₁ (rdt+ rdt+0₁dW!) (²)), Y₁ (rdt+dW+0zdW!"), with Xo xo and Yo =yo. This corresponds to the multi-stock model studied in class, but with notation (X+, Y₁) instead of (S(1), S(2)). Given the model above, the measure P is already the risk-neutral measure (Both stocks have rate of return r). We write σ = 0₁+0%. We consider a swap option, which gives you the right, at time T, to exchange one share of X for one share of Y. That is, the option has payoff F=(Yr-XT). (a) We first assume that r = 0 (for questions (a)-(f)). Write an explicit expression for the process Xt. Reminder before proceeding to question (b): Girsanov's theorem…arrow_forwardProblem 1. Multi-stock model We consider a 2-stock model similar to the one studied in class. Namely, we consider = S(1) S(2) = S(¹) exp (σ1B(1) + (M1 - 0/1 ) S(²) exp (02B(2) + (H₂- M2 where (B(¹) ) +20 and (B(2) ) +≥o are two Brownian motions, with t≥0 Cov (B(¹), B(2)) = p min{t, s}. " The purpose of this problem is to prove that there indeed exists a 2-dimensional Brownian motion (W+)+20 (W(1), W(2))+20 such that = S(1) S(2) = = S(¹) exp (011W(¹) + (μ₁ - 01/1) t) 롱) S(²) exp (021W (1) + 022W(2) + (112 - 03/01/12) t). where σ11, 21, 22 are constants to be determined (as functions of σ1, σ2, p). Hint: The constants will follow the formulas developed in the lectures. (a) To show existence of (Ŵ+), first write the expression for both W. (¹) and W (2) functions of (B(1), B(²)). as (b) Using the formulas obtained in (a), show that the process (WA) is actually a 2- dimensional standard Brownian motion (i.e. show that each component is normal, with mean 0, variance t, and that their…arrow_forward
- The scores of 8 students on the midterm exam and final exam were as follows. Student Midterm Final Anderson 98 89 Bailey 88 74 Cruz 87 97 DeSana 85 79 Erickson 85 94 Francis 83 71 Gray 74 98 Harris 70 91 Find the value of the (Spearman's) rank correlation coefficient test statistic that would be used to test the claim of no correlation between midterm score and final exam score. Round your answer to 3 places after the decimal point, if necessary. Test statistic: rs =arrow_forwardBusiness discussarrow_forwardBusiness discussarrow_forward
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL


