
Concept explainers
Consider the boundary-value problem
Approximate the solution of the differential equation at the interior points of the region with mesh size h =
The approximate solution of the given differential equation
Answer to Problem 1RE
The approximate solution of the differential equation at the interior points of the region is
Explanation of Solution
Formula used:
Calculation:
Consider the given boundary value problem.
For constructing a mesh with size with
Since
Similarly,
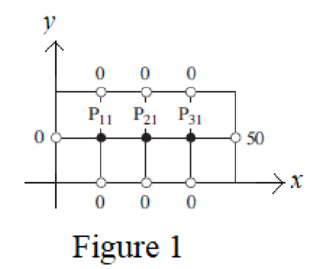
For
From the given boundary conditions
Repeat this for
Since there are less number of unknowns, use Gauss-elimination method to solve the system of equations.
Here, use row column transformations to obtain the values of
Further reduce the matrix as follows.
Therefore, the approximate solution of the differential equation at the interior points of the region is
Want to see more full solutions like this?
Chapter 15 Solutions
Differential Equations with Boundary-Value Problems
- a) show that the empty set and sigletonset are convex set. 6) show that every sub space of linear space X is convex but the convers heed not be true. c) let Mand N be two convex set of a linear Space X and KEF Show that MUN is conevex and (ii) M-N is convex or hot A and is MSN or NSM show that MUN convex or not, 385arrow_forwardxp x+xarrow_forwardFor the given graph, determine the following. -3 12 УА 4 3 - -1 ° 1 2 3 x -1. -2- a. Determine for which values of a the lim f (x) exists but f is not continuous at x = a. a b. Determine for which values of a the function is continuous but not differentiable at x = a. aarrow_forward
- I write with prove one-to-one linear Sanction but not onto Lexample.) b) write with Prove on to linear function but not oh-to-on (example). c) write with prove example x=y St Xandy two linear space over Sielad F.arrow_forwardUse the following graph of ƒ (x) to evaluate ƒ' (−1) and ƒ' (2). y +10+ 9 8 7 6 5 4 3 2 1- -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 x 3 4 0 8 9 10 -2 3 -4 5 -6 -7 -8 -9 -10- f'(-1)= f' (2)arrow_forwardFor the following function f and real number a, a. find the slope of the tangent line mtan = = f' (a), and b. find the equation of the tangent line to f at x = a. f(x) = 2 = ;a=2 a. Slope: b. Equation of tangent line: yarrow_forward
- For the following function f and real number a, a. find the slope of the tangent line mtan = f' (a), and b. find the equation of the tangent line to f at x = a. f(x) = 2x² + 3x; a = 2 a. Slope: b. Equation of tangent line: yarrow_forwardFor the following function f and real number a, find f' (a). f(x) = = √x+4; a = 0 f' (a)arrow_forwardFind the slope of the secant line between the values x₁ and x2 for the function y = f (x). Answer exactly or round to 2 decimal places. f(x) = √√x x7; x₁ = 11, x2 = 23 Slope:arrow_forward
- For the following function f and real number a, find f' (a). f(x)=8x+6; a = −3 f' (a)arrow_forwardFind the slope of the secant line between the values 1 and 2 for the function y = f(x). Answer exactly or round to 2 decimal places. 2 f(x)= ; = x12, x24 2, x2 = 4 2x 1 Slope: Submit Questionarrow_forwardanswer a, b, and carrow_forward
 Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
