
Concept explainers
Find the reaction and plot the shear and bending moment diagram.
Explanation of Solution
Fixed end moment:
Formula to calculate the fixed moment for point load with equal length are
Formula to calculate the fixed moment for point load with unequal length are
Formula to calculate the fixed moment for UDL is
Calculation:
Consider flexural rigidity EI of the beam is constant.
Show the free body diagram of the entire beam as in Figure 1.
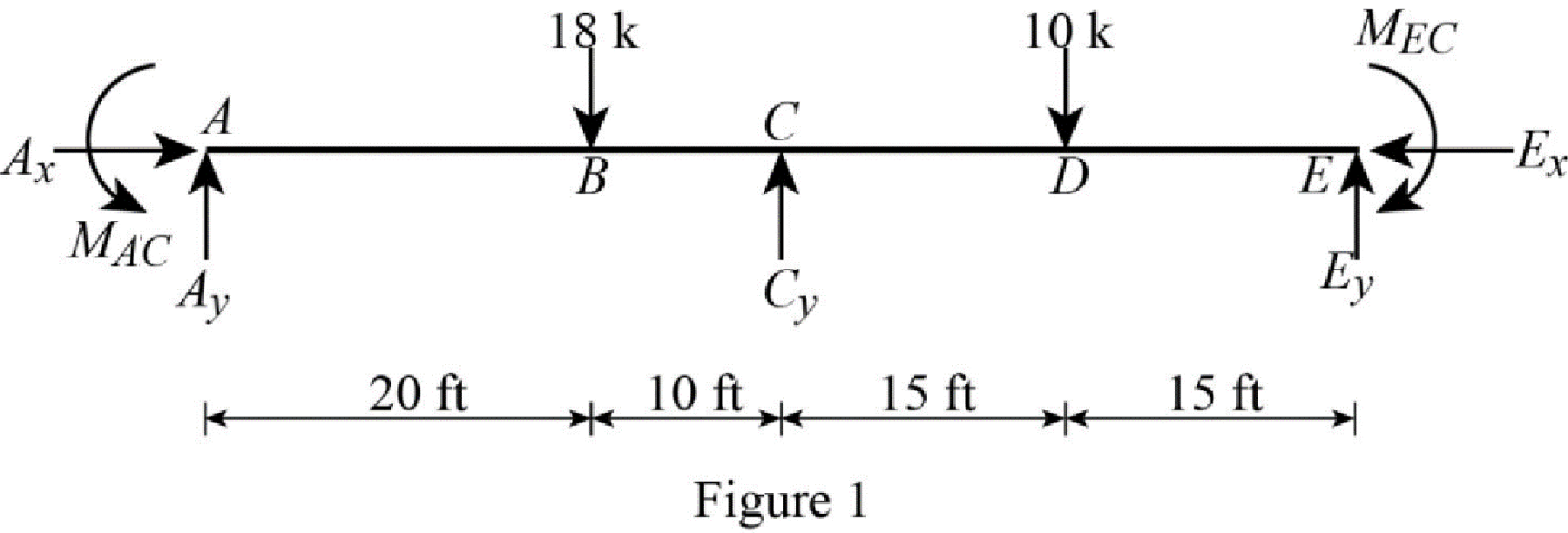
Refer Figure 1,
Calculate the fixed end moment for AC.
Calculate the fixed end moment for CA.
Calculate the fixed end moment for CE.
Calculate the fixed end moment for EC.
Calculate the slope deflection equation for the member AC.
Here,
Substitute 0 for
Calculate the slope deflection equation for the member CA.
Substitute 0 for
Calculate the slope deflection equation for the member CE.
Substitute 0 for
Calculate the slope deflection equation for the member EC.
Substitute 0 for
Write the equilibrium equation as below.
Substitute equation (2) and equation (3) in above equation.
Calculate the moment about AC.
Substitute
Calculate the moment about CA.
Substitute
Calculate the moment about CE.
Substitute
Calculate the moment about EC.
Substitute
Consider the member AC of the beam:
Show the free body diagram of the member AC as in Figure 2.
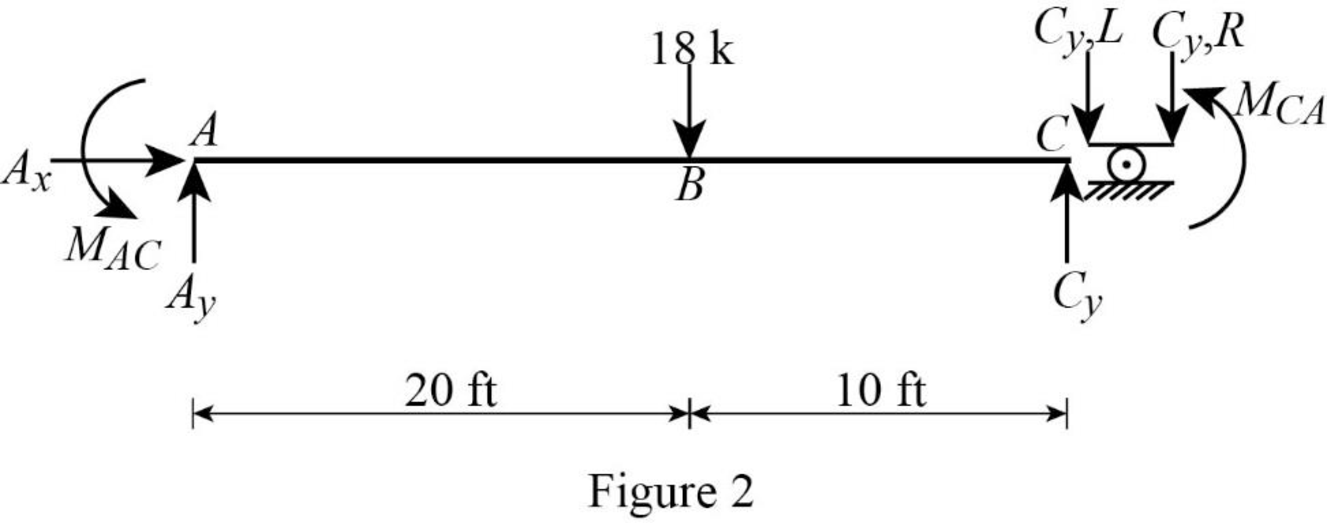
Calculate the vertical reaction at the left end of the joint C by taking moment about point A.
Calculate the horizontal reaction at point A by resolving the horizontal equilibrium.
Calculate the vertical reaction at point A by resolving the vertical equilibrium.
Consider the member CE of the beam:
Show the free body diagram of the member CE as in Figure 2.
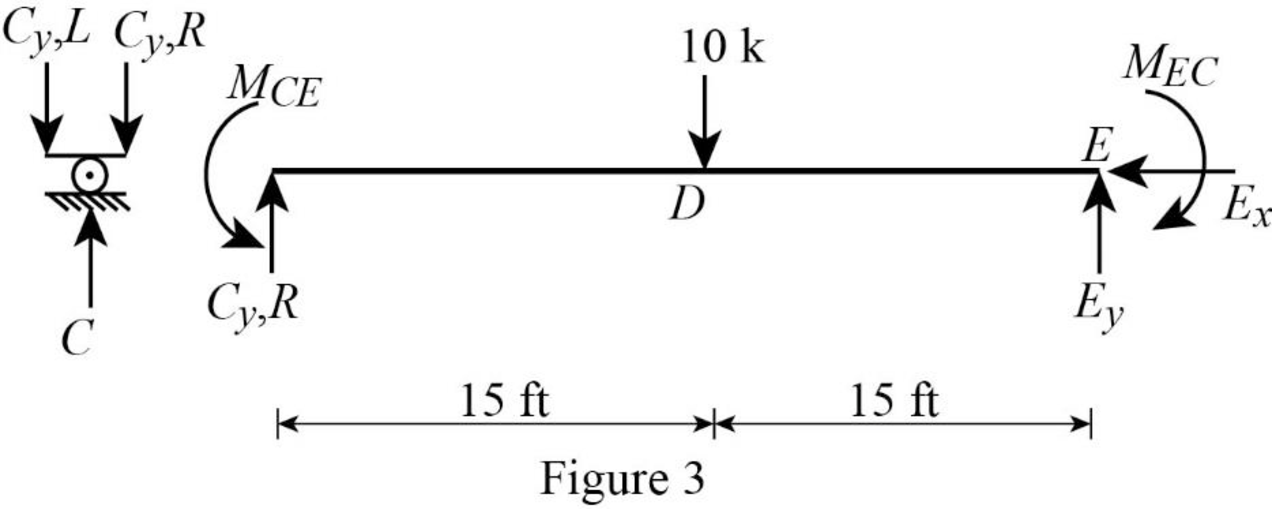
Calculate the vertical reaction at the right end of the joint C by taking moment about point E.
Calculate the horizontal reaction at point E by resolving the horizontal equilibrium.
Calculate the vertical reaction at point E by resolving the vertical equilibrium.
Calculate the total reaction at point C .
Substitute
Show the reaction of the beam in Figure 4.
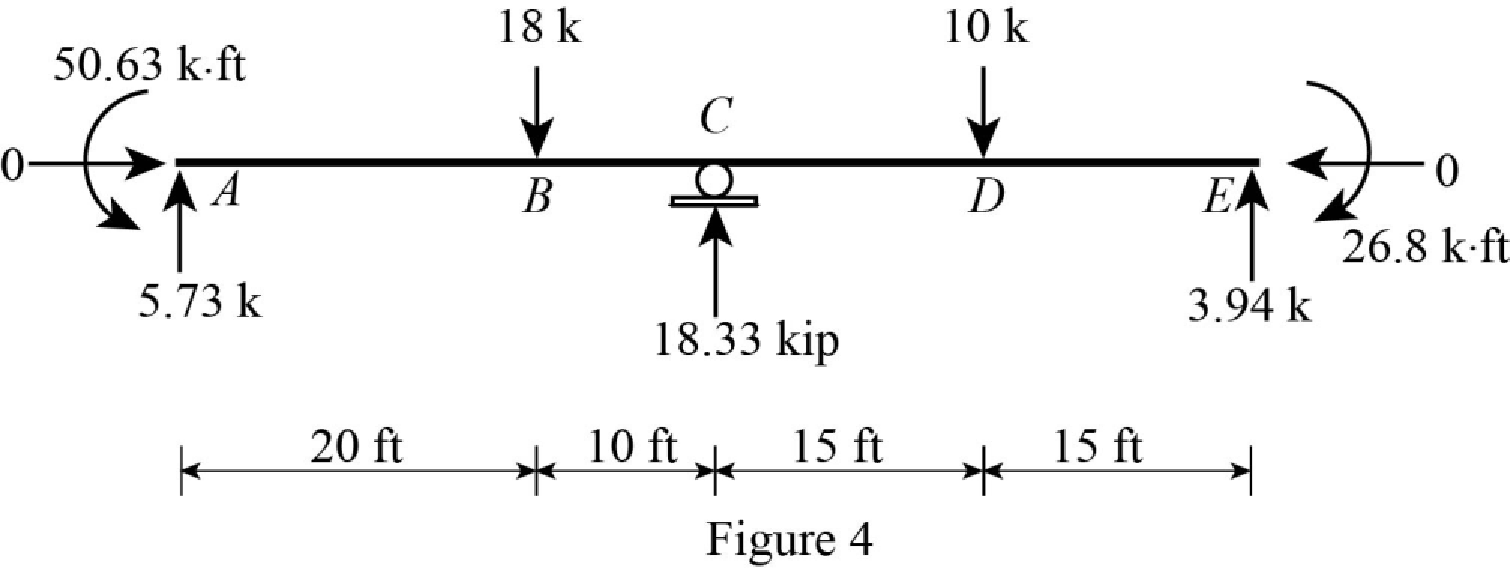
Refer Figure 4,
Shear diagram:
Point A:
Point B:
Point C:
Point D:
Point E:
Plot the shear force diagram of the beam as in Figure 5.
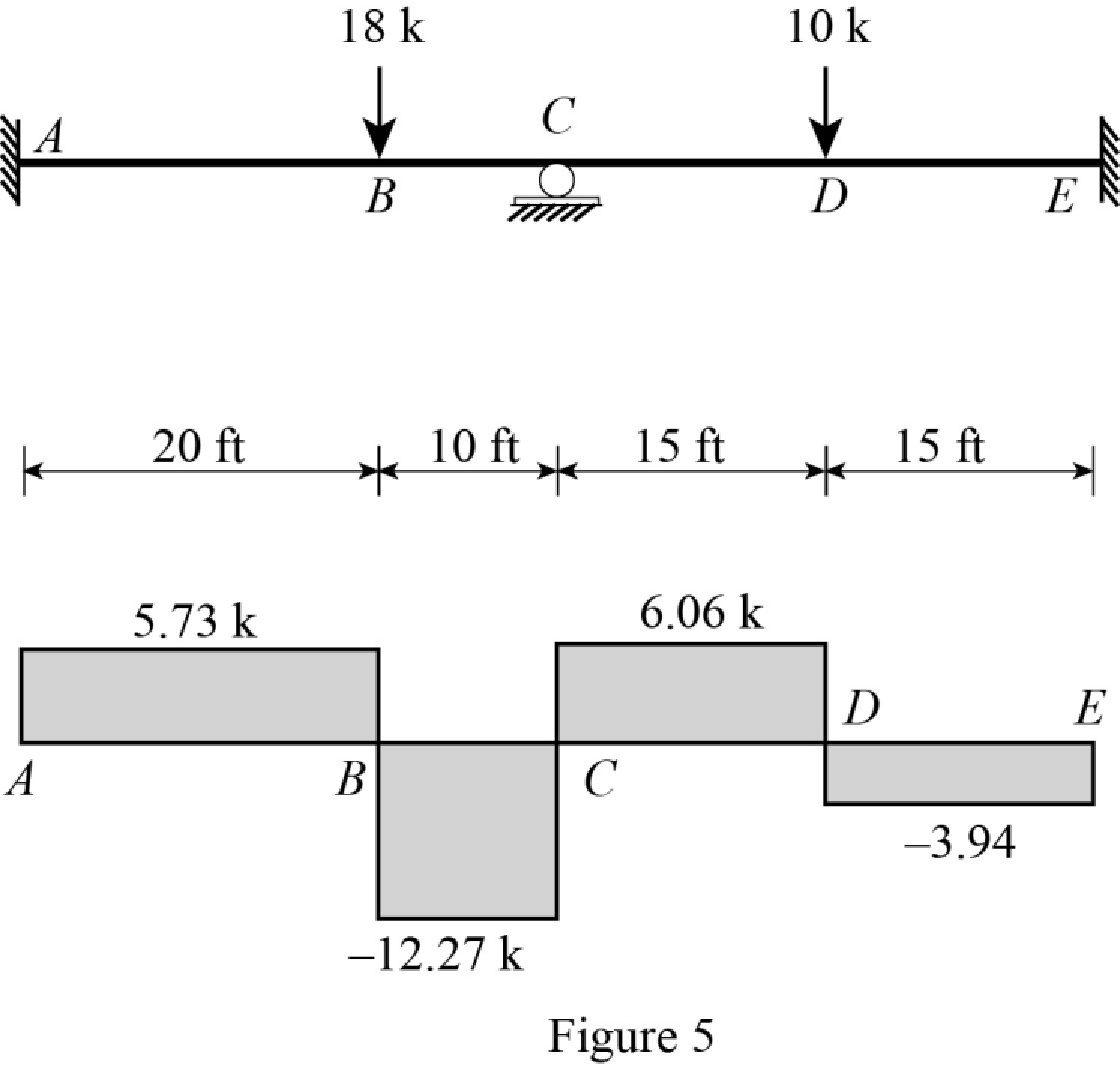
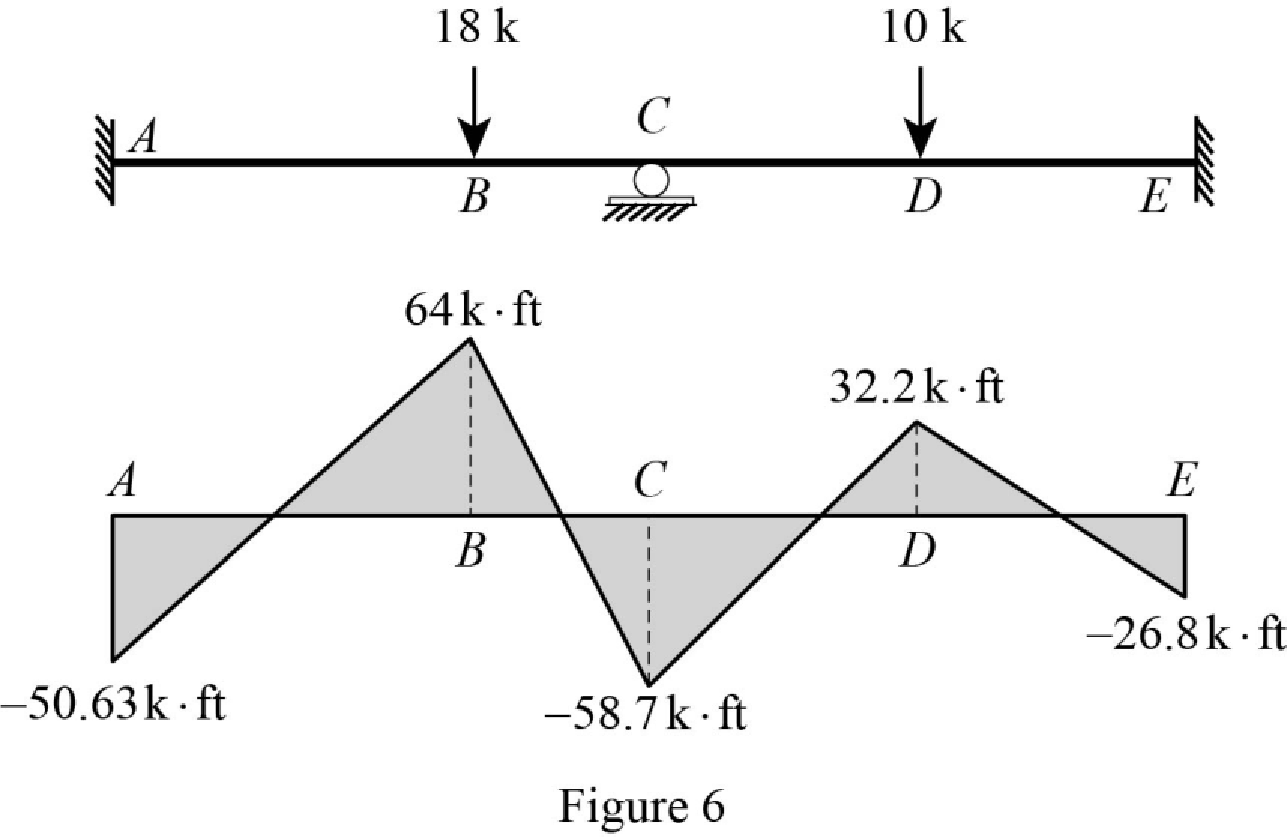
Refer Figure 4,
Bending moment diagram:
Point A:
Point B:
Point C:
Point D:
Point E:
Plot the bending moment diagram of the beam as in Figure 6.
Want to see more full solutions like this?
Chapter 15 Solutions
STRUCTURAL ANALYSIS (LL)
- Problem 4 A propped cantilever beam of flexural rigidity EI and 2EI for parts 1-2 and 2-3, respectively, is subjected to a concentrated load P at point 2. Find: a) Determine the displacement at point 2; b) Determine the rotation at point 3; c) Determine the reaction force and moment at point 1; d) Determine the reaction force at point 3. El 2 P 2 EI 2 Larrow_forwardProblem 3 15 A W150 x 37 rolled-steel beam is used below. Let P150 kN, L-10 m and E 200 GPa. Find the deflection and slope at each node and each pin or wall reaction. If a software program such Maple or MATLAB issued as part of the solution, a hard copy of the code must be submitted too. 1/2 1/2arrow_forward1. Determine the bearings, azimuths, and lengths of lines AB, BC, CD, and DA for the closed loop traverse data shown below in Table 1. Show calculations. Table 1 Station Northing [ft] Easting [ft] A 1,000 1,000 B 750 1,750 C 1,345 2,255 D 1,567 1,345 2. Compute the bearings of sides BC and CD in Figure 1. Show all work for all angles. A B 70°10' S72°39'W C 94°35' Figure 1 Tt (+) B Darrow_forward
- hoph - AT 10x AT 10.076 ht 0.076 0 0-1846112 14884 xh T 1.632m h-4- (1-22) h = 1.022m 14. The 4-ft-diameter cylinder, 4 ft long, is acted upon by water on the left and oil of sp gr 0.800 on the right. Determine (a) the normal force at B if the cylinder weighs 4000 lb and (b) the horizontal force due to oil and water if the oil level drops 1 ft. Solution Water Oil Barrow_forward3. The following data was collected for the traverse shown in Figure 2. a. Determine the latitudes and departures for all sides. b. Determine the linear error of closure and the accuracy ratio. C. Correct and balance the latitudes and departures. A N80°27'E 467.81 ft 497.50 ft N56°46' W B S34°51'E 483.69 ft 325.06 ft D N81°48' Warrow_forwardPlease answer the questions in the picture. Thank you for your help!arrow_forward
- 1500 N A B 3500 N/m 1.2 m 3.6 m 1.2 m 1800 N Beam Cross-section: 4b T D b 25 mm 100 mm For beam ABCD with cross-section shown, design the beam by determining the following: Draw the shear and bending moment diagrams (show your detailed computations to get credit) The minimum dimension for b [mm], knowing that the allowable flexural stress and transverse shear stress are 10 MPa and 0.5 MPa, respectively.arrow_forwardCivil engineering quantiarrow_forwardPlease answer the questions in the picture. Thank you for your help. For part B use the Second Picture.arrow_forward
- Derive by deconvolution the six-hour unit hydrograph from the following data for a watershed having a drainage area of 216 km2 , assuming a constant rainfall abstraction rate and a constant baseflow of 20 m3 /s. Six-hour period 1 2 3 4 5 6 7 8 9 10 11 Rainfall (cm) 1.5 3.5 2.5 1.5 Streamflow (m3 /s) 26 71 174 226 173 99 49 33 26 22 21 Use the unit hydrograph developed to calculate the streamflow hydrographfrom a 12 hour-duration storm having 2 cm of rainfall excess in the first six hours and 3 cm inthe second six hours. Assume a constant baseflow rate of 30 m3/s.arrow_forwardPlease answer the following question in the picture. Thank you for your help.arrow_forwardGiven the unit hydrographic in the table, calculate the streamdlow hydrographic from a 12 hour duration story having 2cm of rainfall excess in the first six hours and 3cm in the second six hours. Assume a constant base flow rate of 30 m3/sarrow_forward
