Chapter 15, Problem 15P

To determine

Find the reaction and plot the shear and bending moment diagram.

Answer to Problem 15P

The end moments at the member A$\left(M_A\right)$, B$\left(M_B\right)$, C$\left(M_C\right)$, and E$\left(M_E\right)$ are $-68.6\text{kN}\cdot \text{m}$, $-183\text{kN}\cdot \text{m}$, $28.9\text{kN}\cdot \text{m}$, and $-170.1\text{kN}\cdot \text{m}$ respectively and the reaction at point A, B, C and E are $\underset{\_}{65.7\text{kN}\uparrow }$, $\underset{\_}{200.8\text{kN}\uparrow }$, $\underset{\_}{56.8\text{kN}\uparrow }$, and $\underset{\_}{54.9\text{kN}\uparrow }$ respectively.

Explanation of Solution

Fixed end moment:

Formula to calculate the fixed moment for point load with equal length are $\frac{PL}{8}$.

Formula to calculate the fixed moment for point load with unequal length are $\frac{Pa{b}^2}{L^2}$ and $\frac{P{a}^{2}b}{L^2}$.

Formula to calculate the fixed moment for UDL is $\frac{W{L}^2}{12}$.

Formula to calculate the fixed moment for deflection is $\frac{6EI\Delta }{L^2}$

Calculation:

Consider the flexural rigidity EI of the beam is constant.

Show the free body diagram of the entire beam as in Figure 1.

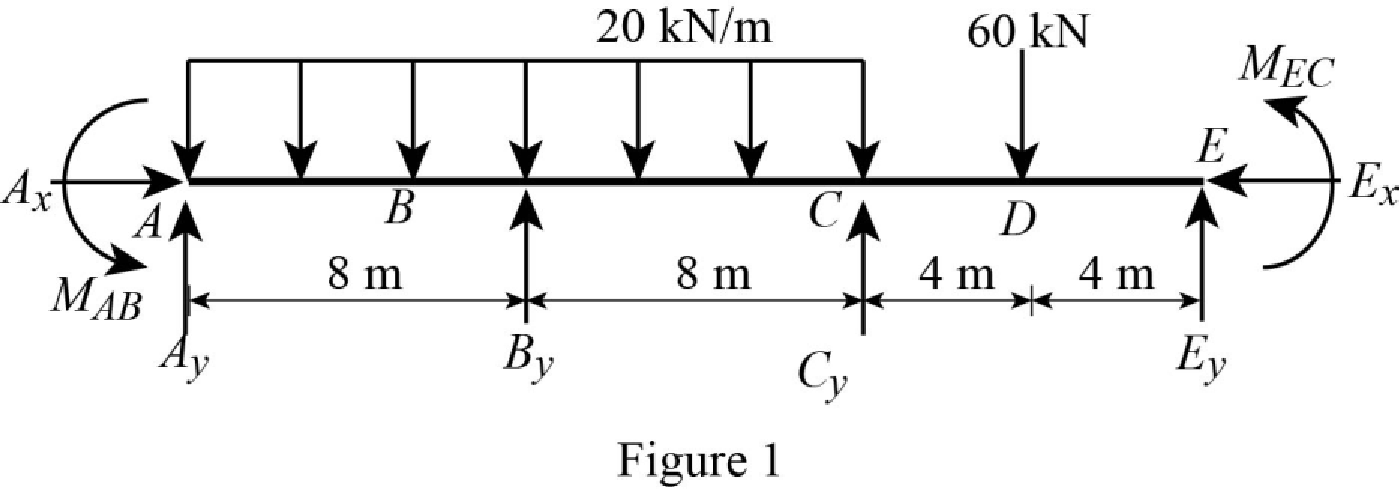
Refer Figure 1,

Calculate the fixed end moment for AB.

$\begin{array}{c}{\text{FEM}}_{AB}=\frac{20\times 8^2}{12}\\ =106.7\text{kN}\cdot \text{m}\end{array}$

Calculate the fixed end moment for BA.

$\begin{array}{c}{\text{FEM}}_{BA}=-\frac{20\times 8^2}{12}\\ =-106.7\text{kN}\cdot \text{m}\end{array}$

Calculate the fixed end moment for BC.

$\begin{array}{c}{\text{FEM}}_{BC}=\frac{20\times 8^2}{12}\\ =106.7\text{kN}\cdot \text{m}\end{array}$

Calculate the fixed end moment for CB.

$\begin{array}{c}{\text{FEM}}_{CB}=-\frac{20\times 8^2}{12}\\ =-106.7\text{kN}\cdot \text{m}\end{array}$

Calculate the fixed end moment for CE.

$\begin{array}{c}{\text{FEM}}_{CE}=\frac{60\times 8}{8}\\ =60\text{kN}\cdot \text{m}\end{array}$

Calculate the fixed end moment for EC.

$\begin{array}{c}{\text{FEM}}_{EC}=-\frac{60\times 8}{8}\\ =-60\text{kN}\cdot \text{m}\end{array}$

Chord rotations:

Show the free body diagram of the chord rotation of the beam as in Figure 2.

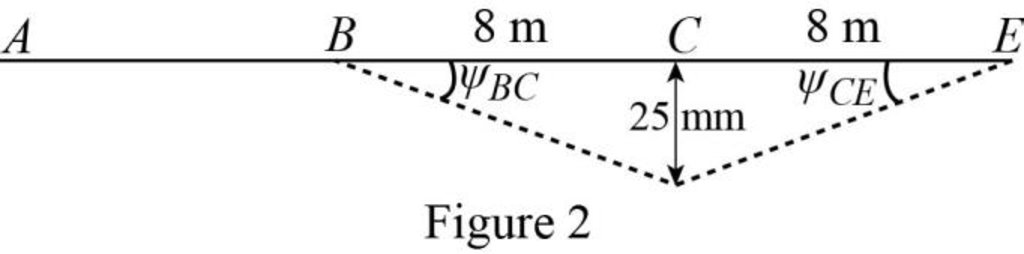
Calculate the chord rotation of the beam BC.

$\begin{array}{c}{\psi }_{BC}=\frac{-25\text{mm}\times \frac{\text{1m}}{\text{1000mm}}}{8\text{m}}\\ =-0.003125\end{array}$

Calculate the chord rotation of the beam CE.

$\begin{array}{c}{\psi }_{CE}=\frac{25\text{mm}\times \frac{\text{1m}}{\text{1000mm}}}{8\text{m}}\\ =0.003125\end{array}$

Calculate the slope deflection equation for the member AB.

$M_{AB}=\frac{2EI}{L}\left(2{\theta }_A+{\theta }_B-3\psi \right)+{\text{FEM}}_{AB}$

Here, $\psi$ is the chord rotation, ${\theta }_A$ is the slope at the point A and ${\theta }_B$ is the slope at the point B.

Substitute $70\text{GPa}$ for E, $800\times {10}^{\text{6}}{\text{mm}}^{\text{4}}$ for I, 0 for ${\theta }_A$, 8 m for L and $106.7\text{kN}\cdot \text{m}$ for ${\text{FEM}}_{AB}$.

$\begin{array}{c}{M}_{AB}=\frac{2\times 70\times 800}{8}\left(2\left(0\right)+{\theta }_B-3\left(0\right)\right)+106.7\\ =14000{\theta }_B+106.7\end{array}$ (1)

Calculate the slope deflection equation for the member BA.

$M_{BA}=\frac{2EI}{L}\left(2{\theta }_B+{\theta }_A-3\psi \right)+{\text{FEM}}_{BA}$

Substitute $70\text{GPa}$ for E, $800\times {10}^{\text{6}}{\text{mm}}^{\text{4}}$ for I, 0 for ${\theta }_A$, 8 m for L and $-106.7\text{kN}\cdot \text{m}$ for ${\text{FEM}}_{BA}$.

$\begin{array}{c}{M}_{BA}=\frac{2\times 70\times 800}{8}\left(2{\theta }_B+0-3\left(0\right)\right)-106.7\\ =28000{\theta }_B-106.7\end{array}$ (2)

Calculate the slope deflection equation for the member BC.

$M_{BC}=\frac{2EI}{L}\left(2{\theta }_B+{\theta }_C-3{\psi }_{BC}\right){\text{+FEM}}_{BC}$

Substitute $70\text{GPa}$ for E, $800\times {10}^{\text{6}}{\text{mm}}^{\text{4}}$ for I, $-0.003125$ for ${\psi }_{BC}$, 8 m for L and $106.7\text{kN}\cdot \text{m}$ for ${\text{FEM}}_{BC}$.

$\begin{array}{c}{M}_{BC}=\frac{2\times 70\times 800}{8}\left(2{\theta }_B+{\theta }_C-\left(3\times -0.003125\right)\right)+106.7\\ =28000{\theta }_B+14000{\theta }_C+131.25+106.7\\ =28000{\theta }_B+14000{\theta }_C+238\end{array}$ (3)

Calculate the slope deflection equation for the member CB.

$M_{CB}=\frac{2EI}{L}\left(2{\theta }_C+{\theta }_B-3{\psi }_{CB}\right){\text{+FEM}}_{CB}$

Substitute $70\text{GPa}$ for E, $800\times {10}^{\text{6}}{\text{mm}}^{\text{4}}$ for I, $-0.003125$ for ${\psi }_{CB}$, 8 m for L and $-106.7\text{kN}\cdot \text{m}$ for ${\text{FEM}}_{CB}$.

$\begin{array}{c}{M}_{CB}=\frac{2\times 70\times 800}{8}\left({\theta }_B+2{\theta }_C-\left(3\times -0.003125\right)\right)-106.7\\ =14000{\theta }_B+28000{\theta }_C+131.25-106.7\\ =14000{\theta }_B+28000{\theta }_C+24.6\end{array}$ (4)

Calculate the slope deflection equation for the member CE.

$M_{CE}=\frac{2EI}{L}\left(2{\theta }_C+{\theta }_E-3{\psi }_{CE}\right){\text{+FEM}}_{CE}$

Substitute $70\text{GPa}$ for E, $800\times {10}^{\text{6}}{\text{mm}}^{\text{4}}$ for I, 0 for ${\theta }_E$, $0.003125$ for ${\psi }_{CE}$, 8 m for L and $60\text{kN}\cdot \text{m}$ for ${\text{FEM}}_{CE}$.

$\begin{array}{c}{M}_{CE}=\frac{2\times 70\times 800}{8}\left(0+2{\theta }_C-\left(3\times 0.003125\right)\right)+60\\ =28000{\theta }_C-131.25+60\\ =28000{\theta }_C-71.3\end{array}$ (5)

Calculate the slope deflection equation for the member EC.

$M_{EC}=\frac{2EI}{L}\left(2{\theta }_E+{\theta }_C-3{\psi }_{EC}\right){\text{+FEM}}_{EC}$

Substitute $70\text{GPa}$ for E, $800\times {10}^{\text{6}}{\text{mm}}^{\text{4}}$ for I, 0 for ${\theta }_E$, $0.003125$ for ${\psi }_{CE}$, 8 m for L and $-60\text{kN}\cdot \text{m}$ for ${\text{FEM}}_{EC}$.

$\begin{array}{c}{M}_{EC}=\frac{2\times 70\times 800}{8}\left({\theta }_C+2\left(0\right)-\left(3\times 0.003125\right)\right)-60\\ =14000{\theta }_C-131.25-60\\ =14000{\theta }_C-191.3\end{array}$ (6)

Write the equilibrium equation as below.

$M_{BA}+M_{BC}=0$

Substitute equation (2) and equation (3) in above equation.

$\begin{array}{l}28000{\theta }_B-106.7+28000{\theta }_B+14000{\theta }_C+238=0\\ 56000{\theta }_B+14000{\theta }_C=-131.3\end{array}$ (7)

Write the equilibrium equation as below.

$M_{CB}+M_{CD}=0$

Substitute equation (4) and equation (5) in above equation.

$\begin{array}{l}14000{\theta }_B+28000{\theta }_C+24.6+28000{\theta }_C-71.3=0\\ 14000{\theta }_B+56000{\theta }_C-46.7=0\\ 14000{\theta }_B+56000{\theta }_C=46.7\end{array}$ (8)

Solve the equation (7) and equation (8).

$\begin{array}{l}{\theta }_B=-2.723\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}\\ {\theta }_C=1.515\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}\end{array}$

Calculate the moment about AB.

Substitute $-2.723\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}$ for ${\theta }_B$ in equation (1).

$\begin{array}{c}{M}_{AB}=14000\left(-2.723\times {10}^{-3}\right)+106.7\\ =68.6\text{kN}\cdot \text{m}\end{array}$

Calculate the moment about BA.

Substitute $-2.723\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}$ for ${\theta }_B$ in equation (2).

$\begin{array}{c}{M}_{BA}=28000\left(-2.723\times {10}^{-3}\right)-106.7\\ =-183\text{kN}\cdot \text{m}\end{array}$

Calculate the moment about BC.

Substitute $-2.723\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}$ for ${\theta }_B$ and $1.515\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}$ for ${\theta }_C$ in equation (3).

$\begin{array}{c}{M}_{BC}=28000\left(-2.723\times {10}^{-3}\right)+14000\left(1.515\times {10}^{-3}\right)+238\\ =183\text{kN}\cdot \text{m}\end{array}$

Calculate the moment about CB.

Substitute $-2.723\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}$ for ${\theta }_B$ and $1.515\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}$ for ${\theta }_C$ in equation (4).

$\begin{array}{c}{M}_{CB}=14000\left(-2.723\times {10}^{-3}\right)+28000\left(1.515\times {10}^{-3}\right)+24.6\\ =28.9\text{kN}\cdot \text{m}\end{array}$

Calculate the moment about CE.

Substitute $1.515\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}$ for ${\theta }_C$ in equation (5).

$\begin{array}{c}{M}_{CE}=28000\left(1.515\times {10}^{-3}\right)-71.3\\ =-28.9\text{kN}\cdot \text{m}\end{array}$

Calculate the moment about EC.

Substitute $1.515\times {10}^{-3}\text{kN}\cdot {\text{m}}^{\text{2}}$ for ${\theta }_C$ in equation (6).

$\begin{array}{c}{M}_{EC}=14000\left(1.515\times {10}^{-3}\right)-191.3\\ =-170.1\text{kN}\cdot \text{m}\end{array}$

Consider the member AB of the beam:

Show the section free body diagram of the member AB, BC and CE as in Figure 3.

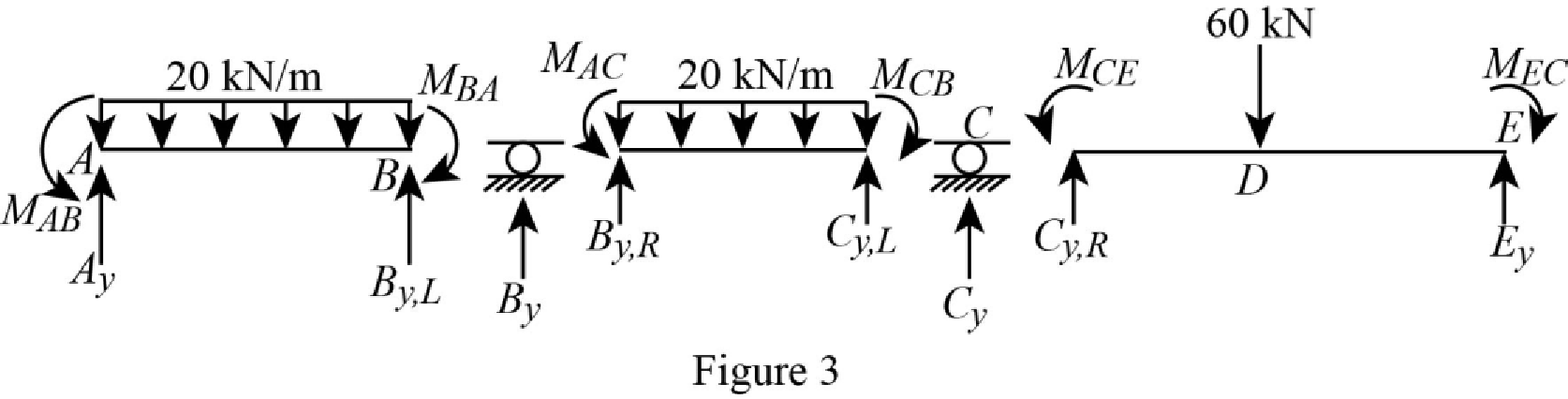
Calculate the vertical reaction at the left end of the joint B by taking moment about point A.

$\begin{array}{l}+\circlearrowleft {\displaystyle \sum M_A=0}\\ B_{y,L}\left(8\right)-20\times \left(8\right)\times \left(\frac{8}{2}\right)+68.6-183=0\\ B_{y,L}\left(8\right)=754.4\\ B_{y,L}=\frac{754.4}{8}\\ B_{y,L}=94.3\text{kN}\end{array}$

Calculate the horizontal reaction at point A by resolving the horizontal equilibrium.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ A_x=0\end{array}$

Calculate the vertical reaction at point A by resolving the vertical equilibrium.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ A_y-\left(20\times 8\right)+B_{y,L}=0\\ A_y-160+94.3=0\\ A_y=65.7\text{kN}\uparrow \end{array}$

Consider the member BC of the beam:

Calculate the vertical reaction at the right end of the joint B by taking moment about point C.

$\begin{array}{l}+\circlearrowleft {\displaystyle \sum M_C=0}\\ B_{y,R}\left(8\right)+20\times \left(8\right)\times \left(\frac{8}{2}\right)+183+28.9=0\\ B_{y,R}\left(8\right)=851.9\\ B_{y,R}=\frac{851.9}{8}\\ B_{y,R}=106.5\text{kN}\uparrow \end{array}$

Calculate the vertical reaction at the left end of joint C by resolving the vertical equilibrium.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ C_{y,L}-\left(20\times 8\right)+B_{y,R}=0\\ C_{y,L}-160+106.5=0\\ C_{y,L}=53.5\text{kN}\uparrow \end{array}$

Calculate the total reaction at point B.

$B_y=B_{y,R}+B_{y,L}$

Substitute $106.5\text{kN}$ for $B_{y,R}$ and $94.3\text{kN}$ for $B_{y,L}$.

$\begin{array}{c}{B}_y=106.5\text{kN}+94.3\text{kN}\\ =200.8\text{kN}\uparrow \end{array}$

Calculate the vertical reaction at the right end of the joint C by taking moment about point E.

$\begin{array}{l}+\circlearrowleft {\displaystyle \sum M_E=0}\\ -C_{y,R}\left(8\right)+60\times \left(4\right)-28.9-170.1=0\\ -C_{y,R}\left(8\right)=41\\ C_{y,R}=\frac{41}{8}\\ C_{y,R}=5.1\text{kN}\uparrow \end{array}$

Calculate the horizontal reaction at point E by resolving the horizontal equilibrium.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ E_x=0\end{array}$

Calculate the vertical reaction at point E by resolving the vertical equilibrium.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ E_y-60+C_{y,R}=0\\ E_y-60+5.1=0\\ E_y=54.9\text{kN}\uparrow \end{array}$

Calculate the total reaction at point C.

$C_y=C_{y,R}+C_{y,L}$

Substitute $5.1\text{kN}$ for $C_{y,R}$ and $53.5\text{kN}$ for $C_{y,L}$.

$\begin{array}{c}{C}_y=5.1\text{kN}+53.5\text{kN}\\ =58.6\text{kN}\uparrow \end{array}$

Show the reactions of the beam in Figure 4.

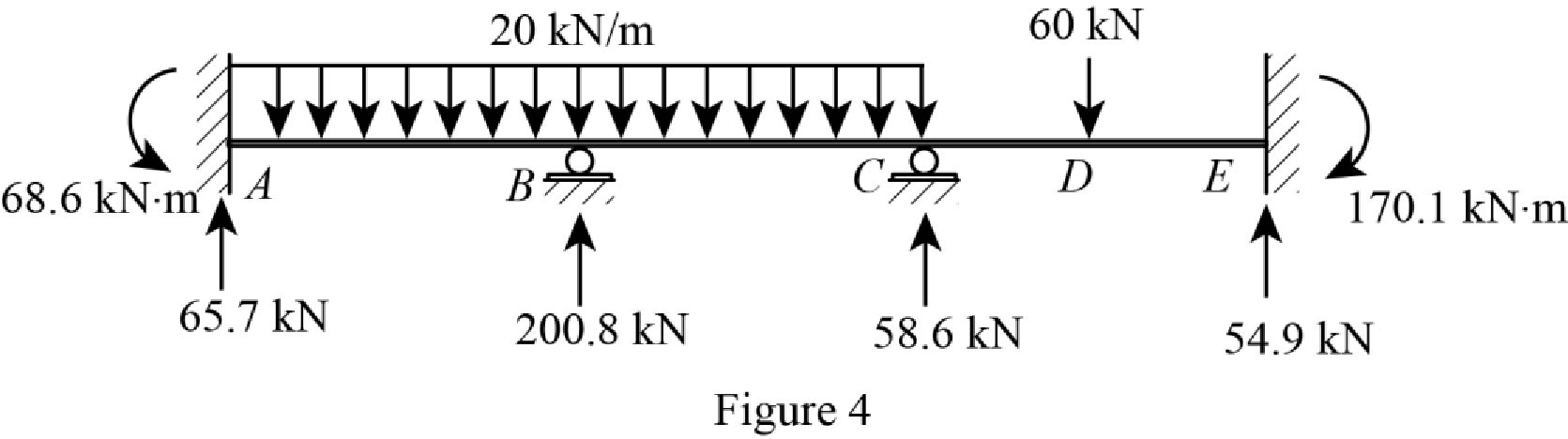
Refer Figure 4,

Shear diagram:

Point A:

$\begin{array}{l}{S}_{A,L}=0\\ S_{A,R}=65.7\text{kN}\end{array}$

Point B:

$\begin{array}{c}{S}_{B,L}=65.7-\left(20\times 8\right)\\ =-94.3\text{kN}\\ S_{B,R}=-94.3\text{kN}+200.8\text{kN}\\ =106.5\text{kN}\end{array}$

Point C:

$\begin{array}{c}{S}_{C,L}=106.5-\left(20\times 8\right)\\ =-53.5\text{kN}\\ S_{C,R}=-53.5+58.6\\ =5.1\text{kN}\end{array}$

Point E:

$\begin{array}{c}{S}_{E,L}=5.1-60\\ =-54.9\text{kN}\\ S_{E,R}=-54.9+25.3\\ =0\text{kN}\end{array}$

Plot the shear force diagram of the beam as in Figure 5.

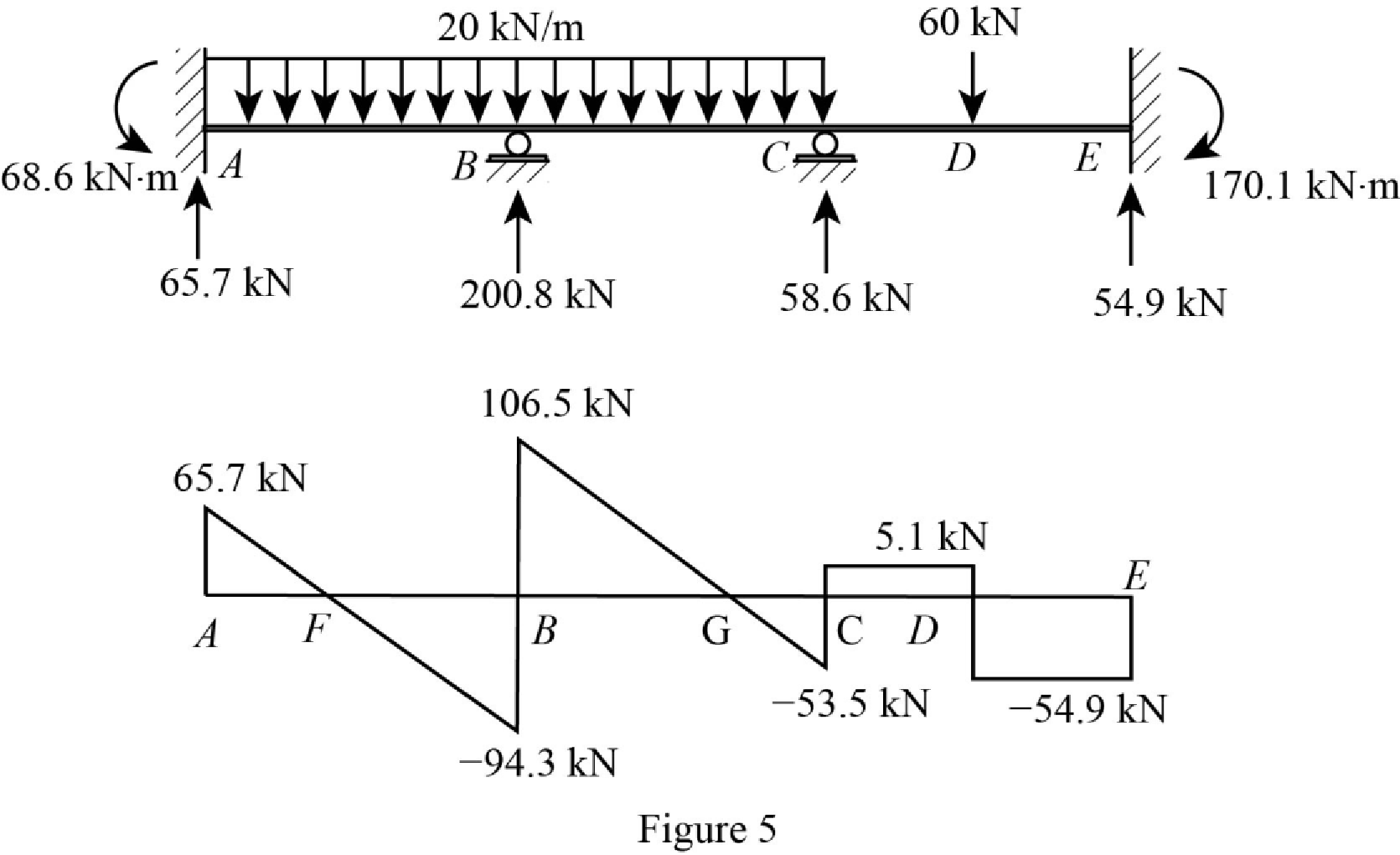
Show the shear diagram of the section AB as in Figure 6.

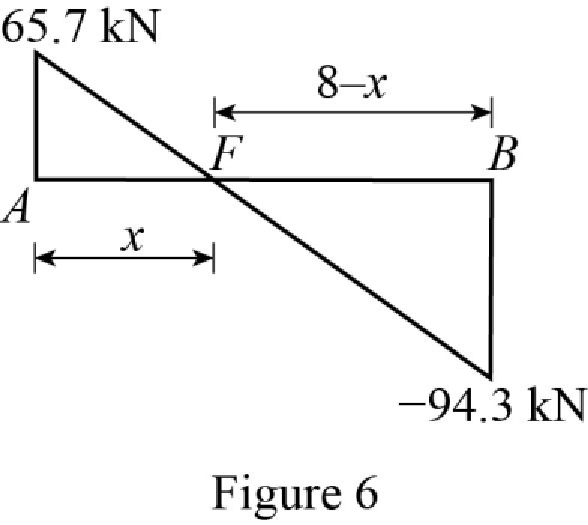
Use the similar triangle concept, to find the location of the maximum bending moment.

$\begin{array}{l}\frac{65.7}{x}=\frac{94.3}{8-x}\\ 525.6-65.7x=94.3x\\ 160x=525.6\\ x=3.3\text{m}\text{from}\text{point }A\end{array}$

Show the shear diagram of the section BC as in Figure 7.

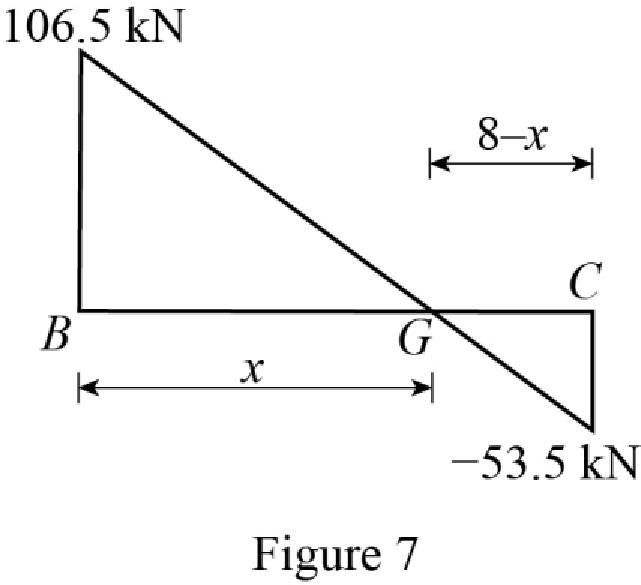
Use the similar triangle concept, to find the location of the maximum bending moment.

$\begin{array}{l}\frac{106.5}{x}=\frac{53.5}{8-x}\\ 852-106.5x=53.5x\\ 160x=852\\ x=5.3\text{m}\text{from}\text{point }B\end{array}$

Refer Figure 4,

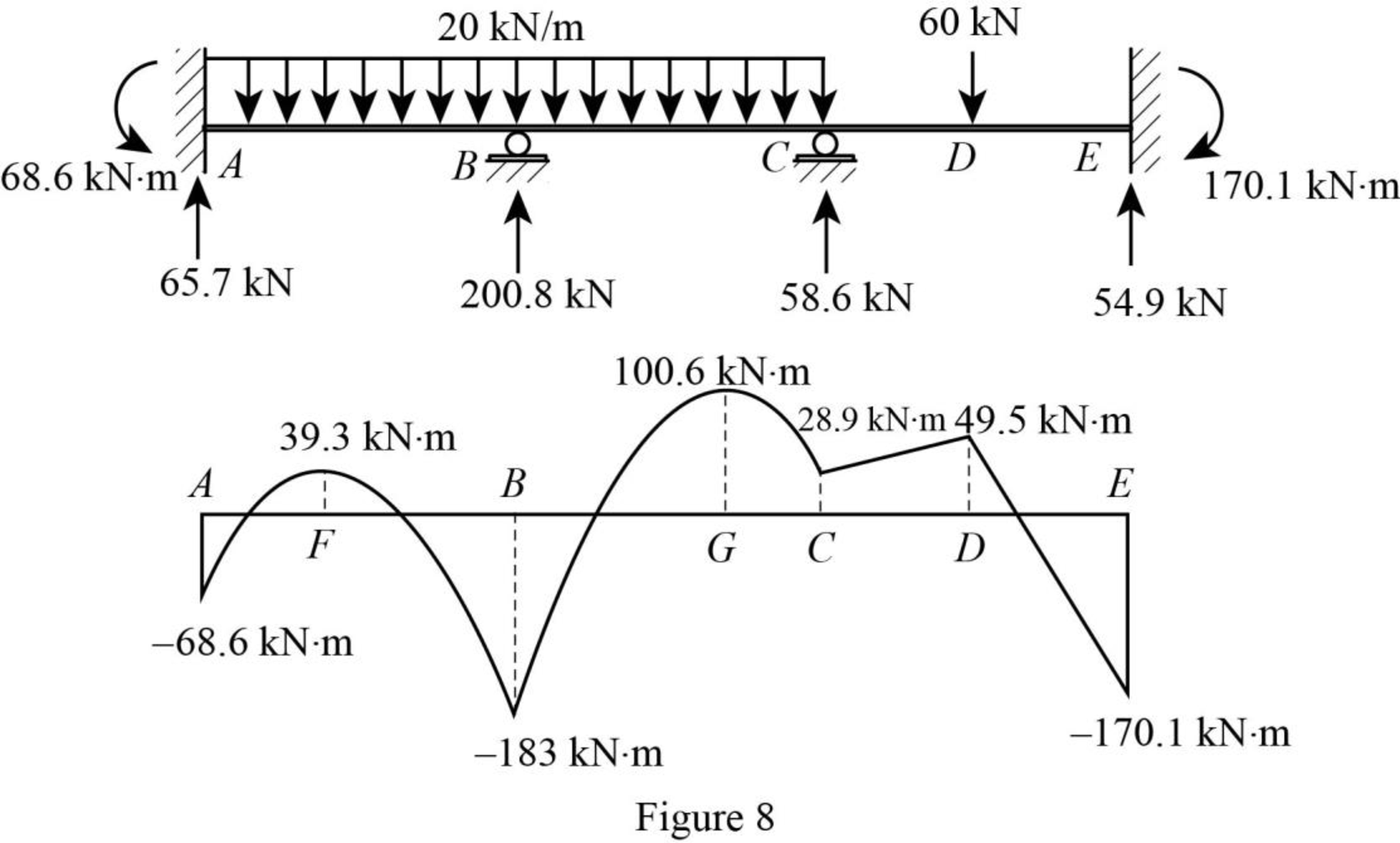
Bending moment diagram:

Point A:

$M_A=-68.6\text{kN}\cdot \text{m}$

Point F:

$\begin{array}{c}{M}_F=-68.6+\left(65.7\times 3.3\right)-\left(20\times 3.3\times \frac{3.3}{2}\right)\\ =39.3\text{kN}\cdot \text{m}\end{array}$

Point B:

$M_B=-183\text{kN}\cdot \text{m}$

Point G:

$\begin{array}{c}{M}_G=68.6-\left(65.7\times 13.3\right)-\left(200.8\times 5.3\right)+\left(20\times 13.3\times \frac{13.3}{2}\right)\\ =100.6\text{kN}\cdot \text{m}\end{array}$

Point C:

$M_C=28.9\text{kN}\cdot \text{m}$

Point D:

$\begin{array}{c}{M}_D=\left(54.9\times 4\right)-170.1\\ =49.5\text{kN}\cdot \text{m}\end{array}$

Point E:

$M_E=-170.1\text{kN}\cdot \text{m}$

Plot the bending moment diagram of the beam as in Figure 8.