
Find a transformation
Want to see the full answer?
Check out a sample textbook solution
Chapter 14 Solutions
Calculus Early Transcendentals, Binder Ready Version
Additional Math Textbook Solutions
Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
Calculus & Its Applications (14th Edition)
Precalculus Enhanced with Graphing Utilities
Calculus: Early Transcendentals (2nd Edition)
Calculus: Single And Multivariable
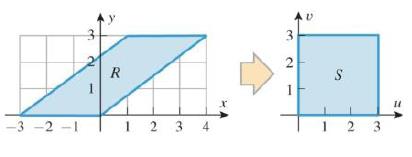
- Use the transformation u = x2 –- y²,v = x² + y² to find ff, xydA where R is the region in the first quadrant that is enclosed by the hyperbolas x2 y² = 1, x² – y² = 4 and the circles x² + y? = 4 and x? + y? = 9.arrow_forwardEvaluate the circulation of G = xyi+zj+7yk around a square of side 9, centered at the origin, lying in the yz-plane, and oriented counterclockwise when viewed from the positive x-axis. Circulation = Prevs So F.dr-arrow_forwardI need answer within 20 minutes please please with my best wishesarrow_forward
- Sketch a diagram of the linear map G that maps the rectangle R = [0, 1]×[0, 1] inthe uv-plane to the parallelogram P in the xy-plane with vertices (0, 0),(2, 2),(1, 4),and (3, 6). Draw the rectangle in the uv-plane on the left and its image P in thexy-plane on the right, with an arrow labeled G in the middle. Find the map G(u, v) = (x(u, v), y(u, v)) explicitly. Set up, but do not evaluate an integral in u and v to calculate Z ZRxy dA.arrow_forwardPls help ASAParrow_forwardLet R = {(x,y): |x| + |y| ≤ 2}. Use the transformation x=u+v, y=u-v to evaluate ∫∫ ((x^2)*(e^y))dAarrow_forward
- Every linear transformation x = au + bv, y = cu + dv with ad – bc + 0 maps lines of the uv-plane onto lines of the xy-plane. Find the image (a) of a vertical line u = uo; (b) of a horizontal line v = vo.arrow_forwardSketch the surface of f(x,y)arrow_forwardUse the transformation u = y - x, v = y, to evaluate the integral on the parallelogram R of vertices (0, 0), (1, 0), (2, 1), and (1, 1) shown in the figure. (y2 - xy) dA 1 0.8 0.6 0.4- 0.2- 0.5 1 1.5arrow_forward
- What kind of transformation results in applying the rule (x, y) → (x - 5, y) in the coordinate plane? (Include the distance and direction.)arrow_forwardFind the image of the rectangular region in the z − plane formed by joining the points0, 0 , 2, 0 , 2, 1 , (0, 1) in the w − plane under the transformation,w = (1 +i )z − 2iInterpret both the regions graphically.arrow_forwardanswer quicklyarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
