
Precalculus Enhanced with Graphing Utilities (7th Edition)
7th Edition
ISBN: 9780134119281
Author: Michael Sullivan, Michael Sullivan III
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 14.3, Problem 13SB
In Problems 7-42, find each limit algebraically.
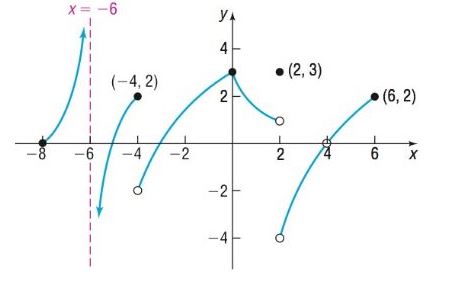
What is the domain of ?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
1. Estimate the area under the graph of
f(x)-25-x from x=0 to x=5 using 5
approximating rectangles Using:
(A) right endpoints.
(B) left endpoints.
9. Use fundamental theorem of calculus to find the
derivative
d
a) *dt
sin(x)
b)(x)√1-2 dt
3. Evaluate the definite integral:
a) √66x²+8dx
b) x dx
c) f*(2e* - 2)dx d) √√9-x²
e) (2-5x)dx
f)
cos(x)dx
8)²₁₂√4-x2
h) f7dx i) f² 6xdx
j) ²₂(4x+3)dx
Chapter 14 Solutions
Precalculus Enhanced with Graphing Utilities (7th Edition)
Ch. 14.1 - Graph f( x )={ 3x2ifx2 3ifx=2 (pp.100-102)Ch. 14.1 - If f( x )={ xifx0 1ifx0 what is f( 0 ) ?...Ch. 14.1 - The limit of a function f( x ) as x approaches c...Ch. 14.1 - If a function f has no limit as x approaches c ,...Ch. 14.1 - True or False lim xc f( x )=N may be described by...Ch. 14.1 - True or False lim xc f( x ) exists and equals some...Ch. 14.1 - lim x2 ( 4 x 3 )Ch. 14.1 - lim x3 ( 2 x 2 +1 )Ch. 14.1 - lim x0 x+1 x 2 +1Ch. 14.1 - lim x0 2x x 2 +4
Ch. 14.1 - lim x4 x 2 4x x4Ch. 14.1 - lim x3 x 2 9 x 2 3xCh. 14.1 - lim x0 ( e x +1 )Ch. 14.1 - Prob. 14SBCh. 14.1 - lim x0 cosx1 x , x in radiansCh. 14.1 - lim x0 tanx x , x in radiansCh. 14.1 - In Problems 17-22, use the graph shown to...Ch. 14.1 - In Problems 17-22, use the graph shown to...Ch. 14.1 - In Problems 17-22, use the graph shown to...Ch. 14.1 - In Problems 17-22, use the graph shown to...Ch. 14.1 - In Problems 17-22, use the graph shown to...Ch. 14.1 - In Problems 17-22, use the graph shown to...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 23-42, graph each function. Use the...Ch. 14.1 - In Problems 43-48, use a graphing utility to find...Ch. 14.1 - In Problems 43-48, use a graphing utility to find...Ch. 14.1 - In Problems 43-48, use a graphing utility to find...Ch. 14.1 - In Problems 43-48, use a graphing utility to find...Ch. 14.1 - In Problems 43-48, use a graphing utility to find...Ch. 14.1 - In Problems 43-48, use a graphing utility to find...Ch. 14.1 - Problems 49-52 are based on material learned...Ch. 14.1 - Problems 49-52 are based on material learned...Ch. 14.1 - Problems 49-52 are based on material learned...Ch. 14.1 - Problems 49-52 are based on material learned...Ch. 14.2 - The limit of the product of two functions equals...Ch. 14.2 - lim xc b= _____Ch. 14.2 - lim xc x= a. x b. c c. cx d. x cCh. 14.2 - True or False The limit of a polynomial function...Ch. 14.2 - True or False The limit of a rational function at...Ch. 14.2 - True or false The limit of a quotient equals the...Ch. 14.2 - In Problems 7- 42, find each limit algebraically....Ch. 14.2 - In Problems 7- 42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 7-42, find each limit algebraically....Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In Problems 43-52, find the limit as x approaches...Ch. 14.2 - In problems 53-56, use the properties of limits...Ch. 14.2 - In problems 53-56, use the properties of limits...Ch. 14.2 - In problems 53-56, use the properties of limits...Ch. 14.2 - In problems 53-56, use the properties of limits...Ch. 14.2 - Problems 57-60 are based on material learned...Ch. 14.2 - Problems 57-60 are based on material learned...Ch. 14.2 - Problems 57-60 are based on material learned...Ch. 14.2 - Problems 57-60 are based on material learned...Ch. 14.3 - For the function f( x )={ x 2 ifx0 x+1if0x2...Ch. 14.3 - What are the domain and range of f( x )=lnx ?Ch. 14.3 - True or False The exponential function f( x )= e x...Ch. 14.3 - Name the trigonometric functions that have...Ch. 14.3 - True or False Some rational functions have holes...Ch. 14.3 - True or False Every polynomial function has a...Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - In Problems 7-42, find each limit algebraically....Ch. 14.3 - Find lim x 4 f( x ) .Ch. 14.3 - Find lim x 4 + f( x ) .Ch. 14.3 - Find lim x 2 f( x ) .Ch. 14.3 - Find lim x 2 + f( x ) .Ch. 14.3 - Does lim x4 f( x ) exist? If it does, what is it?Ch. 14.3 - Does lim x0 f( x ) exist? If it does, what is it?Ch. 14.3 - Is f continuous at 4 ?Ch. 14.3 - Is f continuous at 6 ?Ch. 14.3 - Is f continuous at 0?Ch. 14.3 - Is f continuous at 2?Ch. 14.3 - Is f continuous at 4?Ch. 14.3 - Is f continuous at 5?Ch. 14.3 - lim x 1 + ( 2x+3 )Ch. 14.3 - lim x 2 ( 42x )Ch. 14.3 - lim x 1 ( 2 x 3 +5x )Ch. 14.3 - lim x 2 + ( 3 x 2 8 )Ch. 14.3 - lim x/ 2 + sinxCh. 14.3 - lim x ( 3cosx )Ch. 14.3 - lim x 2 + x 2 4 x2Ch. 14.3 - lim x 1 x 3 x x1Ch. 14.3 - lim x 1 x 2 1 x 3 +1Ch. 14.3 - lim x 0 + x 3 x 2 x 4 + x 2Ch. 14.3 - lim x 2 + x 2 +x2 x 2 +2xCh. 14.3 - lim x 4 x 2 +x12 x 2 +4xCh. 14.3 - f( x )= x 3 3 x 2 +2x6c=2Ch. 14.3 - f( x )=3 x 2 6x+5c=3Ch. 14.3 - f( x )= x 2 +5 x6 c=3Ch. 14.3 - f( x )= x 3 8 x 2 +4 c=2Ch. 14.3 - f( x )= x+3 x3 c=3Ch. 14.3 - f( x )= x6 x+6 c=6Ch. 14.3 - f( x )= x 3 +3x x 2 3x c=0Ch. 14.3 - f( x )= x 2 6x x 2 +6x c=0Ch. 14.3 - f( x )={ x 3 +3x x 2 3x ifx0 1ifx=0 c=0Ch. 14.3 - f( x )={ x 2 6x x 2 +6x ifx0 2ifx=0 c=0Ch. 14.3 - f( x )={ x 3 +3x x 2 3x ifx0 1ifx=0 c=0Ch. 14.3 - f( x )={ x 2 6x x 2 +6x ifx0 1ifx=0 c=0Ch. 14.3 - f( x )={ x 3 1 x 2 1 ifx1 2ifx=1 3 x+1 ifx1 c=1Ch. 14.3 - f( x )={ x 2 2x x2 ifx2 2ifx=2 x4 x1 ifx2 c=2Ch. 14.3 - f( x )={ 2 e x ifx0 2ifx=0 x 3 +2 x 2 x 2 ifx0 c=0Ch. 14.3 - f( x )={ 3cosxifx0 3ifx=0 x 3 +3 x 2 x 2 ifx0 c=0Ch. 14.3 - f( x )=2x+3Ch. 14.3 - f( x )=43xCh. 14.3 - f( x )=3 x 2 +xCh. 14.3 - f( x )=3 x 3 +7Ch. 14.3 - f( x )=4sinxCh. 14.3 - f( x )=2cosxCh. 14.3 - f( x )=2tanxCh. 14.3 - f( x )=4cscxCh. 14.3 - f( x )= 2x+5 x 2 4Ch. 14.3 - f( x )= x 2 4 x 2 9Ch. 14.3 - f( x )= x3 InxCh. 14.3 - f( x )= lnx x3Ch. 14.3 - R( x )= x1 x 2 1 , c=1 and c=1Ch. 14.3 - R( x )= 3x+6 x 2 4 , c=2 and c=2Ch. 14.3 - R( x )= x 2 +x x 2 1 , c=1 and c=1Ch. 14.3 - R( x )= x 2 +4x x 2 16 , c=4 and c=4Ch. 14.3 - R( x )= x 3 x 2 +x1 x 4 x 3 +2x2Ch. 14.3 - R( x )= x 3 + x 2 +3x+3 x 4 + x 3 +2x+2Ch. 14.3 - R( x )= x 3 2 x 2 +4x8 x 2 +x6Ch. 14.3 - R( x )= x 3 x 2 +3x3 x 2 +3x4Ch. 14.3 - R( x )= x 3 +2 x 2 +x x 4 + x 3 +2x+2Ch. 14.3 - R( x )= x 3 3 x 2 +4x12 x 4 3 x 3 +x3Ch. 14.3 - R( x )= x 3 x 2 +x1 x 4 x 3 +2x2 Graph R(x) .Ch. 14.3 - R( x )= x 3 + x 2 +3x+3 x 4 + x 3 +2x+2 Graph R( x...Ch. 14.3 - R(x)= ( x 3 2 x 2 +4x8) ( x 2 +x6) Graph R( x ) .Ch. 14.3 - Prob. 86SBCh. 14.3 - Prob. 87SBCh. 14.3 - Prob. 88SBCh. 14.3 - Prob. 89DWCh. 14.3 - Prob. 90DWCh. 14.3 - Prob. 91RYKCh. 14.3 - Evaluate the permutation P( 5,3 ) .Ch. 14.3 - Prob. 93RYKCh. 14.3 - Prob. 94RYKCh. 14.4 - Find an equation of the line with slope 5...Ch. 14.4 - Prob. 2AYPCh. 14.4 - Prob. 3CVCh. 14.4 - Prob. 4CVCh. 14.4 - Prob. 5CVCh. 14.4 - Prob. 6CVCh. 14.4 - Prob. 7CVCh. 14.4 - Prob. 8CVCh. 14.4 - Prob. 9SBCh. 14.4 - Prob. 10SBCh. 14.4 - Prob. 11SBCh. 14.4 - Prob. 12SBCh. 14.4 - Prob. 13SBCh. 14.4 - Prob. 14SBCh. 14.4 - Prob. 15SBCh. 14.4 - Prob. 16SBCh. 14.4 - Prob. 17SBCh. 14.4 - Prob. 18SBCh. 14.4 - Prob. 19SBCh. 14.4 - Prob. 20SBCh. 14.4 - Prob. 21SBCh. 14.4 - Prob. 22SBCh. 14.4 - Prob. 23SBCh. 14.4 - Prob. 24SBCh. 14.4 - Prob. 25SBCh. 14.4 - Prob. 26SBCh. 14.4 - Prob. 27SBCh. 14.4 - Prob. 28SBCh. 14.4 - Prob. 29SBCh. 14.4 - Prob. 30SBCh. 14.4 - Prob. 31SBCh. 14.4 - f( x )=cosx at 0Ch. 14.4 - Prob. 33SBCh. 14.4 - Prob. 34SBCh. 14.4 - Prob. 35SBCh. 14.4 - Prob. 36SBCh. 14.4 - Prob. 37SBCh. 14.4 - Prob. 38SBCh. 14.4 - Prob. 39SBCh. 14.4 - Prob. 40SBCh. 14.4 - Prob. 41SBCh. 14.4 - Prob. 42SBCh. 14.4 - Prob. 43AECh. 14.4 - Prob. 44AECh. 14.4 - Prob. 45AECh. 14.4 - Prob. 46AECh. 14.4 - Prob. 47AECh. 14.4 - Instantaneous Velocity of a Ball In physics it is...Ch. 14.4 - Instantaneous Velocity on the Moon Neil Armstrong...Ch. 14.4 - Instantaneous Rate of Change The following data...Ch. 14.4 - Prob. 51RYKCh. 14.4 - Prob. 52RYKCh. 14.4 - Prob. 53RYKCh. 14.4 - Prob. 54RYKCh. 14.5 - In Problems 29-32, find the first five terms in...Ch. 14.5 - Prob. 2AYPCh. 14.5 - Prob. 3CVCh. 14.5 - Prob. 4CVCh. 14.5 - Prob. 5SBCh. 14.5 - Prob. 6SBCh. 14.5 - Prob. 7SBCh. 14.5 - Prob. 8SBCh. 14.5 - Prob. 9SBCh. 14.5 - Repeat Problem 9 for f( x )=4x .Ch. 14.5 - Prob. 11SBCh. 14.5 - Prob. 12SBCh. 14.5 - Prob. 13SBCh. 14.5 - Prob. 14SBCh. 14.5 - Prob. 15SBCh. 14.5 - Prob. 16SBCh. 14.5 - Prob. 17SBCh. 14.5 - Prob. 18SBCh. 14.5 - Prob. 19SBCh. 14.5 - Prob. 20SBCh. 14.5 - Prob. 21SBCh. 14.5 - Prob. 22SBCh. 14.5 - Prob. 23SBCh. 14.5 - Prob. 24SBCh. 14.5 - Prob. 25SBCh. 14.5 - Prob. 26SBCh. 14.5 - Prob. 27SBCh. 14.5 - Prob. 28SBCh. 14.5 - Prob. 29SBCh. 14.5 - Prob. 30SBCh. 14.5 - Prob. 31SBCh. 14.5 - Consider the function f( x )= 1 x 2 whose domain...Ch. 14.5 - Graph the function f( x )= log 2 x .Ch. 14.5 - If A=[ 1 2 3 4 ] and B=[ 5 6 0 7 8 1 ] , find AB .Ch. 14.5 - If f( x )=2 x 2 +3x+1 , find f( x+h )f( x ) h and...Ch. 14.5 - Prob. 36RYK
Additional Math Textbook Solutions
Find more solutions based on key concepts
Percentiles. In Exercises 17-20, use the following cell phone airport data speeds (Mbps) from Sprint. Find the ...
Elementary Statistics (13th Edition)
a. Fill in the missing numbers in the following factor tree. b. How could you find the top numbers without find...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
The equivalent expression of x(y+z) by using the commutative property.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
For a population containing N=902 individual, what code number would you assign for a. the first person on the ...
Basic Business Statistics, Student Value Edition
Using the Empirical Rule In Exercises 29–34, use the Empirical Rule.
34. The monthly utility bills for eight ho...
Elementary Statistics: Picturing the World (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 2. Consider the integral √(2x+1)dx (a) Find the Riemann sum for this integral using right endpoints and n-4. (b) Find the Riemann sum for this same integral, using left endpoints and n=4arrow_forward5. For the function y-x³-3x²-1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (e) determine the intervals of concavity. (d) determine the points of inflection. (e) sketch the graph with the above information indicated on the graph.arrow_forwardProblem 11 (a) A tank is discharging water through an orifice at a depth of T meter below the surface of the water whose area is A m². The following are the values of a for the corresponding values of A: A 1.257 1.390 x 1.50 1.65 1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650 1.80 1.95 2.10 2.25 2.40 2.55 2.70 2.85 Using the formula -3.0 (0.018)T = dx. calculate T, the time in seconds for the level of the water to drop from 3.0 m to 1.5 m above the orifice. (b) The velocity of a train which starts from rest is given by the fol- lowing table, the time being reckoned in minutes from the start and the speed in km/hour: | † (minutes) |2|4 6 8 10 12 14 16 18 20 v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0 Estimate approximately the total distance ran in 20 minutes.arrow_forward
- 8–23. Sketching vector fields Sketch the following vector fieldsarrow_forward25-30. Normal and tangential components For the vector field F and curve C, complete the following: a. Determine the points (if any) along the curve C at which the vector field F is tangent to C. b. Determine the points (if any) along the curve C at which the vector field F is normal to C. c. Sketch C and a few representative vectors of F on C. 25. F = (2½³, 0); c = {(x, y); y − x² = 1} 26. F = x (23 - 212) ; C = {(x, y); y = x² = 1}) , 2 27. F(x, y); C = {(x, y): x² + y² = 4} 28. F = (y, x); C = {(x, y): x² + y² = 1} 29. F = (x, y); C = 30. F = (y, x); C = {(x, y): x = 1} {(x, y): x² + y² = 1}arrow_forward٣/١ B msl kd 180 Ka, Sin (1) I sin () sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 G 5005 1000 s = 1000-950 Copper bosses 5kW Rotor input 5 0.05 : loo kw 6) 1 /0001 ined sove in peaper I need a detailed solution on paper please وه اذا ميريد شرح الكتب فقط ١٥٠ DC 7) rotor a ' (y+xlny + xe*)dx + (xsiny + xlnx + dy = 0. Q1// Find the solution of: ( 357arrow_forward
- ۳/۱ R₂ = X2 2) slots per pole per phase 3/31 B. 180 msl Kas Sin (I) 1sin() sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30): 0.866 4) Rotating 5) Synchronous speeds 120×50 looo G 1000-950 1000 Copper losses 5kw Rotor input 5 loo kw 0.05 6) 1 اذا ميريد شرح الكتب فقط look 7) rotor DC ined sove in peaper I need a detailed solution on paper please 0 64 Find the general solution of the following equations: QI//y(4)-16y= 0. Find the general solution of the following equations: Q2ll yll-4y/ +13y=esinx.arrow_forwardR₂ = X2 2) slots per pole per phase = 3/31 B-180 60 msl kd Kas Sin () 2 I sin (6) sin(30) Sin (30) اذا مريد شرح الكتب بس 0 بالفراغ 3 Cos (30) 0.866 4) Rotating ined sove in peaper 5) Synchronous speed s 120×50 6 s = 1000-950 1000 Copper losses 5kw Rotor input 5 0.05 6) 1 loo kw اذا ميريد شرح الكتب فقط Look 7) rotov DC I need a detailed solution on paper please 0 64 Solve the following equations: 0 Q1// Find the solution of: ( y • with y(0) = 1. dx x²+y²arrow_forwardR₂ = X2 2) slots per pole per phase = 3/3 1 B-180-60 msl Ka Sin (1) Isin () sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 s = 1000-950 1000 Copper losses 5kw Rotor input 5 6) 1 0.05 G 50105 loo kw اذا ميريد شرح الكتب فقط look 7) rotov DC ined sove in peaper I need a detailed solution on paper please 064 2- A hot ball (D=15 cm ) is cooled by forced air T.-30°C, the rate of heat transfer from the ball is 460.86 W. Take for the air -0.025 Wim °C and Nu=144.89, find the ball surface temperature a) 300 °C 16 b) 327 °C c) 376 °C d) None か = 750 01arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning

College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY