
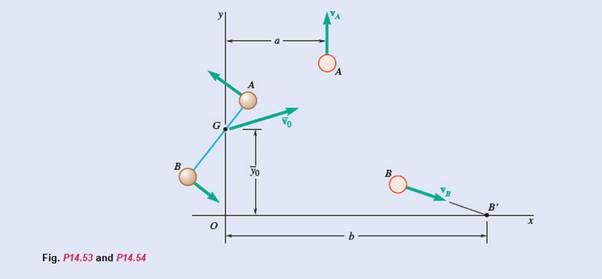
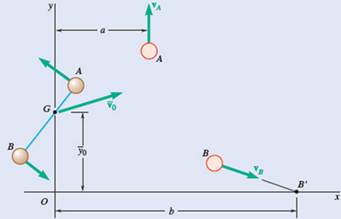
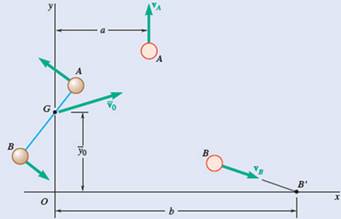
Two small disks A and B of mass 3 kg and 1.5 kg, respectively, may slide on a horizontal, frictionless surface. They are connected by a cord, 600 mm long, and spin counterclockwise about their mass center G at the rate of 10 rad/s. At t = 0, the coordinates of G are
'
(a)
The velocities of disks A and B after the cord breaks.
Answer to Problem 14.53P
Explanation of Solution
Given information:
Mass of the disk A,
Mass of the disk B,
Length of cord
At t=0,
Co-ordinates of G are
Velocity
Distance
Firstly, calculate for initial condition.
The free body diagram for initial condition is as follows:
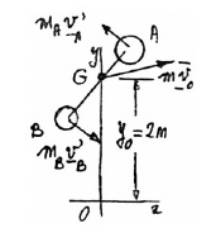
The distance G from points A and B,
And,
Now, considering linear momentum,
After breaking the disks moves counter clockwise about their mass centre G, at the rate of 10 rad/sec.
Hence, angular momentum of both the disc about G,
Again, angular momentum of both the disc about point O,
Here, the property of determinant
Now, kinetic energy of the component is,
Calculation:
After the cord is break then the free body diagram of both disc A and B.
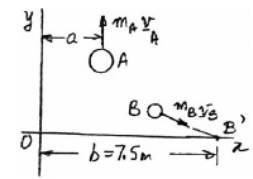
Using conservation of mass of linear momentum,
Equation the coefficient of i :
Equation the coefficient of j :
Applying conservation of energy,
Substituting the values from equation (1) and (2);
By solving the above equation we get;
Hence, velocity of A,
And velocity of B,
(b)
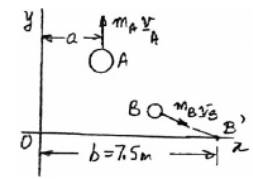
The distance a from the y-axis to the path of A.
Answer to Problem 14.53P
Explanation of Solution
Given information:
Mass of the disk A,
Mass of the disk B,
Length of cord
At t=0,
Co-ordinates of G are
Velocity,
Distance
Firstly, calculate for initial condition.
The free body diagram for initial condition is as follows:
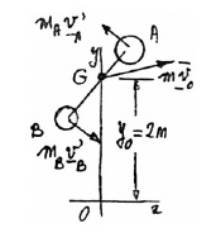
The distance G from points A and B,
And,
Now, considering linear momentum,
After breaking the disks moves counter clockwise about their mass centre G, at the rate of 10 rad/sec.
Hence, angular momentum of both the disc about G,
Again, angular momentum of both the disc about point O,
Here, the property of determinant
Now, kinetic energy of the component is,
Calculation:
After the cord is break then the free body diagram of both disc A and B.
Using conservation of mass of linear momentum,
Equation the coefficient of i :
Equation the coefficient of j :
Applying conservation of energy,
Substituting the values from equation (1) and (2);
By solving the above equation we get;
Hence, velocity of A,
And velocity of B,
Now, Conservation of angular momentum about O,
Want to see more full solutions like this?
Chapter 14 Solutions
Vector Mechanics For Engineers