
Calculus
7th Edition
ISBN: 9781337553032
Author: Larson, Ron, Edwards, Bruce H.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 13.5, Problem 48E
HOW DO YOU SEE IT? The path of an object represented by
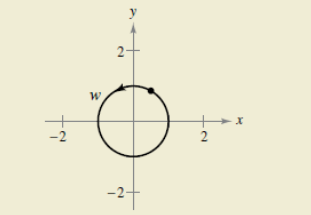
Determine whether each of the following is positive, negative, or zero.
(a)
(b)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
i need help please
6.
(i)
Sketch the trace of the following curve on R²,
(t) = (sin(t), 3 sin(t)),
tЄ [0, π].
[3 Marks]
Total marks 10
(ii)
Find the length of this curve.
[7 Marks]
helppp
Chapter 13 Solutions
Calculus
Ch. 13.1 - Think About It Explain why z2=x+3y is not a...Ch. 13.1 - Function of Two Variables What is a graph of a...Ch. 13.1 - Determine whether graph is a function. Use the...Ch. 13.1 - Contour Map Explain how to sketch a contour map of...Ch. 13.1 - Determining Whether an Equation Is a Function In...Ch. 13.1 - Determining Whether an Equation Is a Function In...Ch. 13.1 - Determining Whether an Equation Is a Function In...Ch. 13.1 - Determining Whether an Equation Is a Function In...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...
Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Evaluating a Function In Exercises 9-20, evaluate...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Finding the Domain and Range of a Function In...Ch. 13.1 - Think About It The graphs labeled (a), (b). (c)....Ch. 13.1 - Prob. 34ECh. 13.1 - Prob. 35ECh. 13.1 - Prob. 36ECh. 13.1 - Sketching a Surface In Exercises 35-42, describe...Ch. 13.1 - Prob. 38ECh. 13.1 - Prob. 39ECh. 13.1 - Prob. 40ECh. 13.1 - Prob. 41ECh. 13.1 - Sketching a Surface In Exercises 35-42, describe...Ch. 13.1 - Graphing a Function Using Technology In Exercises...Ch. 13.1 - Graphing a Function Using Technology In Exercises...Ch. 13.1 - Graphing a Function Using Technology In Exercises...Ch. 13.1 - Graphing a Function Using Technology In Exercises...Ch. 13.1 - Matching In Exercises 47-50, match the graph of...Ch. 13.1 - Matching In Exercises 47-50, match the graph of...Ch. 13.1 - Matching In Exercises 47-50, match the graph of...Ch. 13.1 - Matching In Exercises 47-50, match the graph of...Ch. 13.1 - Sketching a Contour Map In Exercises 51-58,...Ch. 13.1 - Sketching a Contour Map In Exercises 51-58,...Ch. 13.1 - Sketching a Contour Map In Exercises 51-58,...Ch. 13.1 - Sketching a Contour Map In Exercises 51-58,...Ch. 13.1 - Sketching a Contour Map In Exercises 51-58,...Ch. 13.1 - Sketching a Contour Map In Exercises 51-58,...Ch. 13.1 - Sketching a Contour Map In Exercises 51-58,...Ch. 13.1 - Sketching a Contour Map In Exercises 51-58,...Ch. 13.1 - Graphing Level Curves Using Technology In...Ch. 13.1 - Graphing Level Curves Using Technology In...Ch. 13.1 - Graphing Level Curves Using Technology In...Ch. 13.1 - Graphing Level Curves Using Technology In...Ch. 13.1 - Vertical Line Test Does die Vertical Line Test...Ch. 13.1 - Using Level Curves All of the level curves of the...Ch. 13.1 - Creating a Function Construct a function whose...Ch. 13.1 - Conjecture Consider the function f(x,y)=xy, for...Ch. 13.1 - Writing In Exercises 67 and 68, use the graphs of...Ch. 13.1 - Writing In Exercises 67 and 68, use the graphs of...Ch. 13.1 - Investment In 2016, an investment of S1000 was...Ch. 13.1 - Investment A principal of $5000 is deposited in a...Ch. 13.1 - Sketching a Level Surface In Exercises 71-76....Ch. 13.1 - Sketching a Level Surface In Exercises 71-76....Ch. 13.1 - Sketching a Level Surface In Exercises 71-76....Ch. 13.1 - Sketching a Level Surface In Exercises 71-76....Ch. 13.1 - Sketching a Level Surface In Exercises 71-76....Ch. 13.1 - Sketching a Level Surface In Exercises 71-76....Ch. 13.1 - Forestry The Doyle Lux Rule is one of several...Ch. 13.1 - Queuing Model The average length of time that a...Ch. 13.1 - Temperature Distribution The temperature T (in...Ch. 13.1 - Electric Potential The electric potential V at any...Ch. 13.1 - Prob. 81ECh. 13.1 - Cobb-Douglas Production Function In Exercises 81...Ch. 13.1 - Prob. 83ECh. 13.1 - Cobb-Douglas Production Function Show that the...Ch. 13.1 - Ideal Gas Law According to the Ideal Gas Law, PV=...Ch. 13.1 - Prob. 86ECh. 13.1 - Prob. 87ECh. 13.1 - Acid Rain The acidity of rainwater is measured in...Ch. 13.1 - Prob. 89ECh. 13.1 - HOW DO YOU SEE IT? The contour map of the Southern...Ch. 13.1 - Prob. 91ECh. 13.1 - Prob. 92ECh. 13.1 - Prob. 93ECh. 13.1 - Prob. 94ECh. 13.1 - Prob. 95ECh. 13.2 - CONCEPT CHECK Describing Notation Write a brief...Ch. 13.2 - Prob. 2ECh. 13.2 - Prob. 3ECh. 13.2 - Prob. 4ECh. 13.2 - Verifying a Limit by the Definition In Exercises...Ch. 13.2 - Prob. 6ECh. 13.2 - Prob. 7ECh. 13.2 - Prob. 8ECh. 13.2 - Prob. 9ECh. 13.2 - Prob. 10ECh. 13.2 - Prob. 11ECh. 13.2 - Prob. 12ECh. 13.2 - Prob. 13ECh. 13.2 - Prob. 14ECh. 13.2 - Prob. 15ECh. 13.2 - Prob. 16ECh. 13.2 - Prob. 17ECh. 13.2 - Prob. 18ECh. 13.2 - Prob. 19ECh. 13.2 - Prob. 20ECh. 13.2 - Prob. 21ECh. 13.2 - Prob. 22ECh. 13.2 - Prob. 23ECh. 13.2 - Prob. 24ECh. 13.2 - Prob. 25ECh. 13.2 - Prob. 26ECh. 13.2 - Finding a Limit In Exercises 25-36, find the limit...Ch. 13.2 - Prob. 28ECh. 13.2 - Prob. 29ECh. 13.2 - Prob. 30ECh. 13.2 - Prob. 31ECh. 13.2 - Prob. 32ECh. 13.2 - Prob. 33ECh. 13.2 - Prob. 34ECh. 13.2 - Prob. 35ECh. 13.2 - Prob. 36ECh. 13.2 - Prob. 37ECh. 13.2 - Prob. 38ECh. 13.2 - Prob. 39ECh. 13.2 - Prob. 40ECh. 13.2 - Prob. 41ECh. 13.2 - Prob. 42ECh. 13.2 - Prob. 43ECh. 13.2 - Prob. 44ECh. 13.2 - Prob. 45ECh. 13.2 - Prob. 46ECh. 13.2 - Limit Consider lim(x,y)(0,0)x2+y2xy (see figure)....Ch. 13.2 - Prob. 48ECh. 13.2 - Prob. 49ECh. 13.2 - Prob. 50ECh. 13.2 - Prob. 51ECh. 13.2 - Prob. 52ECh. 13.2 - Prob. 53ECh. 13.2 - Prob. 54ECh. 13.2 - Prob. 55ECh. 13.2 - Prob. 56ECh. 13.2 - Prob. 57ECh. 13.2 - Prob. 58ECh. 13.2 - Finding a Limit Using Polar Coordinates In...Ch. 13.2 - Finding a Limit Using Polar Coordinates In...Ch. 13.2 - Prob. 61ECh. 13.2 - Prob. 62ECh. 13.2 - Continuity In Exercises 61-66, discuss the...Ch. 13.2 - Continuity In Exercises 61-66, discuss the...Ch. 13.2 - Prob. 65ECh. 13.2 - Prob. 66ECh. 13.2 - Prob. 67ECh. 13.2 - Prob. 68ECh. 13.2 - Prob. 69ECh. 13.2 - Prob. 70ECh. 13.2 - Prob. 71ECh. 13.2 - Prob. 72ECh. 13.2 - Prob. 73ECh. 13.2 - Prob. 74ECh. 13.2 - Finding a Limit In Exercises 71-76, find each...Ch. 13.2 - Finding a Limit In Exercises 71-76, find each...Ch. 13.2 - Finding a Limit Using Spherical Coordinates In...Ch. 13.2 - Finding a Limit Using Spherical Coordinates In...Ch. 13.2 - Prob. 79ECh. 13.2 - True or False? In Exercises 79-82, determine...Ch. 13.2 - Prob. 81ECh. 13.2 - Prob. 82ECh. 13.2 - Prob. 83ECh. 13.2 - Prob. 84ECh. 13.2 - Prob. 85ECh. 13.2 - Prob. 86ECh. 13.3 - Prob. 1ECh. 13.3 - Prob. 2ECh. 13.3 - Prob. 3ECh. 13.3 - Prob. 4ECh. 13.3 - Prob. 5ECh. 13.3 - Prob. 6ECh. 13.3 - Prob. 7ECh. 13.3 - Prob. 8ECh. 13.3 - Prob. 9ECh. 13.3 - Prob. 10ECh. 13.3 - Prob. 11ECh. 13.3 - Prob. 12ECh. 13.3 - Prob. 13ECh. 13.3 - Prob. 14ECh. 13.3 - Prob. 15ECh. 13.3 - Prob. 16ECh. 13.3 - Prob. 17ECh. 13.3 - Prob. 18ECh. 13.3 - Prob. 19ECh. 13.3 - Prob. 20ECh. 13.3 - Prob. 21ECh. 13.3 - Prob. 22ECh. 13.3 - Prob. 23ECh. 13.3 - Prob. 24ECh. 13.3 - Prob. 25ECh. 13.3 - Prob. 26ECh. 13.3 - Prob. 27ECh. 13.3 - Prob. 28ECh. 13.3 - Prob. 29ECh. 13.3 - Prob. 30ECh. 13.3 - Prob. 31ECh. 13.3 - Prob. 32ECh. 13.3 - Prob. 33ECh. 13.3 - Prob. 34ECh. 13.3 - Prob. 35ECh. 13.3 - Prob. 36ECh. 13.3 - Prob. 37ECh. 13.3 - Prob. 38ECh. 13.3 - Prob. 39ECh. 13.3 - Prob. 40ECh. 13.3 - Prob. 41ECh. 13.3 - Prob. 42ECh. 13.3 - Prob. 43ECh. 13.3 - Prob. 44ECh. 13.3 - Prob. 45ECh. 13.3 - Prob. 46ECh. 13.3 - Prob. 47ECh. 13.3 - Prob. 48ECh. 13.3 - Prob. 49ECh. 13.3 - Prob. 50ECh. 13.3 - Prob. 51ECh. 13.3 - Prob. 52ECh. 13.3 - Prob. 53ECh. 13.3 - Prob. 54ECh. 13.3 - Prob. 55ECh. 13.3 - Prob. 56ECh. 13.3 - Prob. 57ECh. 13.3 - Prob. 58ECh. 13.3 - Prob. 59ECh. 13.3 - Prob. 60ECh. 13.3 - Prob. 61ECh. 13.3 - Prob. 62ECh. 13.3 - Prob. 63ECh. 13.3 - Prob. 64ECh. 13.3 - Prob. 65ECh. 13.3 - Prob. 66ECh. 13.3 - Prob. 67ECh. 13.3 - Prob. 68ECh. 13.3 - Prob. 69ECh. 13.3 - Prob. 70ECh. 13.3 - Prob. 71ECh. 13.3 - Prob. 72ECh. 13.3 - Prob. 73ECh. 13.3 - Prob. 74ECh. 13.3 - Prob. 75ECh. 13.3 - Prob. 76ECh. 13.3 - Prob. 77ECh. 13.3 - Prob. 78ECh. 13.3 - Prob. 79ECh. 13.3 - Prob. 80ECh. 13.3 - Prob. 81ECh. 13.3 - Prob. 82ECh. 13.3 - Prob. 83ECh. 13.3 - Prob. 84ECh. 13.3 - Prob. 85ECh. 13.3 - Prob. 86ECh. 13.3 - Prob. 87ECh. 13.3 - Prob. 88ECh. 13.3 - Prob. 89ECh. 13.3 - Prob. 90ECh. 13.3 - Prob. 91ECh. 13.3 - Prob. 92ECh. 13.3 - Prob. 93ECh. 13.3 - Prob. 94ECh. 13.3 - Prob. 95ECh. 13.3 - Prob. 96ECh. 13.3 - Prob. 97ECh. 13.3 - Prob. 98ECh. 13.3 - Prob. 99ECh. 13.3 - Wave Equation In Exercises 99-102, show that the...Ch. 13.3 - Prob. 101ECh. 13.3 - Prob. 102ECh. 13.3 - Heat Equation In Exercises 103 and 104, show that...Ch. 13.3 - Prob. 104ECh. 13.3 - Prob. 105ECh. 13.3 - Cauchy-Riemann Equations In Exercises 105 and 106,...Ch. 13.3 - Prob. 107ECh. 13.3 - Prob. 108ECh. 13.3 - Prob. 109ECh. 13.3 - Prob. 110ECh. 13.3 - Prob. 111ECh. 13.3 - Prob. 112ECh. 13.3 - Prob. 113ECh. 13.3 - Prob. 114ECh. 13.3 - Prob. 115ECh. 13.3 - Prob. 116ECh. 13.3 - Prob. 117ECh. 13.3 - Prob. 118ECh. 13.3 - Prob. 119ECh. 13.3 - Prob. 120ECh. 13.3 - Prob. 121ECh. 13.3 - Investment The value of an investment of $1000...Ch. 13.3 - Prob. 123ECh. 13.3 - Apparent Temperature A measure of how hot weather...Ch. 13.3 - Prob. 125ECh. 13.3 - Prob. 126ECh. 13.3 - Prob. 127ECh. 13.3 - Prob. 128ECh. 13.3 - Prob. 129ECh. 13.3 - Prob. 130ECh. 13.3 - Prob. 131ECh. 13.4 - CONCEPT CHECK Approximation Describe the change in...Ch. 13.4 - Prob. 2ECh. 13.4 - Prob. 3ECh. 13.4 - Prob. 4ECh. 13.4 - Prob. 5ECh. 13.4 - Finding a Total Differential find the total...Ch. 13.4 - Finding a Total Differential find the total...Ch. 13.4 - Prob. 8ECh. 13.4 - Prob. 9ECh. 13.4 - Prob. 10ECh. 13.4 - Using a Differential as an Approximation In...Ch. 13.4 - Prob. 12ECh. 13.4 - Prob. 13ECh. 13.4 - Prob. 14ECh. 13.4 - Approximating an Expression In Exercises 15-18,...Ch. 13.4 - Prob. 16ECh. 13.4 - Approximating an Expression In Exercises 15-18,...Ch. 13.4 - Prob. 18ECh. 13.4 - Continuity If fx. and fy are each continuous in an...Ch. 13.4 - Prob. 20ECh. 13.4 - Prob. 21ECh. 13.4 - Volume The volume of the red right circular...Ch. 13.4 - Prob. 23ECh. 13.4 - Volume The possible error involved in measuring...Ch. 13.4 - Prob. 25ECh. 13.4 - Prob. 26ECh. 13.4 - Wind Chill The formula for wind chill C (in...Ch. 13.4 - Prob. 28ECh. 13.4 - Prob. 29ECh. 13.4 - Prob. 30ECh. 13.4 - Volume A trough is 16 feet long (see figure). Its...Ch. 13.4 - Sports A baseball player in center field is...Ch. 13.4 - Inductance The inductance L (in microhenrys) of a...Ch. 13.4 - Prob. 34ECh. 13.4 - Prob. 35ECh. 13.4 - Prob. 36ECh. 13.4 - Prob. 37ECh. 13.4 - Differentiability In Exercises 35-38, show that...Ch. 13.4 - Prob. 39ECh. 13.4 - Differentiability In Exercises 39 and 40, use the...Ch. 13.5 - Prob. 1ECh. 13.5 - Prob. 2ECh. 13.5 - Using the Chain Rule In Exercises 3-6, find dw/dt...Ch. 13.5 - Using the Chain Rule In Exercises 3-6, find dw/dt...Ch. 13.5 - Using the Chain Rule In Exercises 3-6, find dw/dt...Ch. 13.5 - Using the Chain Rule In Exercises 3-6, find dw/dt...Ch. 13.5 - Prob. 7ECh. 13.5 - Prob. 8ECh. 13.5 - Using Different Methods In Exercises 7-12, find...Ch. 13.5 - Using Different Methods In Exercises 7-12, find...Ch. 13.5 - Prob. 11ECh. 13.5 - Using Different Methods In Exercises 7-12, find...Ch. 13.5 - Projectile Motion In Exercises 13 and 14, the...Ch. 13.5 - Prob. 14ECh. 13.5 - Prob. 15ECh. 13.5 - Prob. 16ECh. 13.5 - Prob. 17ECh. 13.5 - Prob. 18ECh. 13.5 - Prob. 19ECh. 13.5 - Prob. 20ECh. 13.5 - Prob. 21ECh. 13.5 - Using Different Methods In Exercises 19-22, find...Ch. 13.5 - Prob. 23ECh. 13.5 - Prob. 24ECh. 13.5 - Prob. 25ECh. 13.5 - Finding a Derivative Implicitly In Exercises...Ch. 13.5 - Prob. 27ECh. 13.5 - Prob. 28ECh. 13.5 - Prob. 29ECh. 13.5 - Prob. 30ECh. 13.5 - Prob. 31ECh. 13.5 - Prob. 32ECh. 13.5 - Prob. 33ECh. 13.5 - Prob. 34ECh. 13.5 - Prob. 35ECh. 13.5 - Prob. 36ECh. 13.5 - Prob. 37ECh. 13.5 - Prob. 38ECh. 13.5 - Prob. 39ECh. 13.5 - Prob. 40ECh. 13.5 - Homogeneous Functions A function f is homogeneous...Ch. 13.5 - Prob. 42ECh. 13.5 - Using a Table of Values Let w=f(x,y),x=g(t), and...Ch. 13.5 - Prob. 44ECh. 13.5 - Prob. 45ECh. 13.5 - Prob. 46ECh. 13.5 - Prob. 47ECh. 13.5 - HOW DO YOU SEE IT? The path of an object...Ch. 13.5 - Prob. 49ECh. 13.5 - Prob. 50ECh. 13.5 - Moment of Inertia An annular cylinder has an...Ch. 13.5 - Volume and Surface Area The two radii of the...Ch. 13.5 - Prob. 53ECh. 13.5 - Cauchy-Riemann Equations Demonstrate the result of...Ch. 13.5 - Prob. 55ECh. 13.6 - CONCEPT CHECK Directional Derivative For a...Ch. 13.6 - Prob. 2ECh. 13.6 - Prob. 3ECh. 13.6 - Prob. 4ECh. 13.6 - Prob. 5ECh. 13.6 - Prob. 6ECh. 13.6 - Prob. 7ECh. 13.6 - Prob. 8ECh. 13.6 - Prob. 9ECh. 13.6 - Prob. 10ECh. 13.6 - Prob. 11ECh. 13.6 - Prob. 12ECh. 13.6 - Prob. 13ECh. 13.6 - Prob. 14ECh. 13.6 - Prob. 15ECh. 13.6 - Prob. 16ECh. 13.6 - Finding the Gradient of a Function In Exercises...Ch. 13.6 - Prob. 18ECh. 13.6 - Prob. 19ECh. 13.6 - Prob. 20ECh. 13.6 - Prob. 21ECh. 13.6 - Prob. 22ECh. 13.6 - Prob. 23ECh. 13.6 - Prob. 24ECh. 13.6 - Prob. 25ECh. 13.6 - Prob. 26ECh. 13.6 - Prob. 27ECh. 13.6 - Prob. 28ECh. 13.6 - Prob. 29ECh. 13.6 - Prob. 30ECh. 13.6 - Using Properties of the Gradient In Exercises...Ch. 13.6 - Prob. 32ECh. 13.6 - Prob. 33ECh. 13.6 - Prob. 34ECh. 13.6 - Using Properties of the Gradient In Exercises...Ch. 13.6 - Prob. 36ECh. 13.6 - Prob. 37ECh. 13.6 - Prob. 38ECh. 13.6 - Prob. 39ECh. 13.6 - Prob. 40ECh. 13.6 - Prob. 41ECh. 13.6 - Prob. 42ECh. 13.6 - Prob. 43ECh. 13.6 - Prob. 44ECh. 13.6 - Prob. 45ECh. 13.6 - Prob. 46ECh. 13.6 - Using a Function Consider the function...Ch. 13.6 - Prob. 48ECh. 13.6 - Prob. 49ECh. 13.6 - Prob. 50ECh. 13.6 - Prob. 51ECh. 13.6 - Prob. 52ECh. 13.6 - Topography The surface of a mountain is modeled by...Ch. 13.6 - Prob. 54ECh. 13.6 - Temperature The temperature at the point (x, y) on...Ch. 13.6 - Prob. 56ECh. 13.6 - Prob. 57ECh. 13.6 - Prob. 58ECh. 13.6 - Prob. 59ECh. 13.6 - Finding the Path of a Heat-Seeking Particle In...Ch. 13.6 - Prob. 61ECh. 13.6 - True or False? In Exercises 61-64, determine...Ch. 13.6 - Prob. 63ECh. 13.6 - Prob. 64ECh. 13.6 - Prob. 65ECh. 13.6 - Ocean Floor A team of oceanographers is mapping...Ch. 13.6 - Prob. 67ECh. 13.6 - Prob. 68ECh. 13.7 - CONCEPT CHECK Tangent Vector Consider a point...Ch. 13.7 - Prob. 2ECh. 13.7 - Describing a Surface In Exercises 3-6, describe...Ch. 13.7 - Prob. 4ECh. 13.7 - Describing a Surface In Exercises 3-6, describe...Ch. 13.7 - Describing a Surface In Exercises 3-6, describe...Ch. 13.7 - Finding an Equation of a Tangent Plane In...Ch. 13.7 - Finding an Equation of a Tangent Plane In...Ch. 13.7 - Finding an Equation of a Tangent Plane In...Ch. 13.7 - Prob. 10ECh. 13.7 - Finding an Equation of a Tangent Plane In...Ch. 13.7 - Finding an Equation of a Tangent Plane In...Ch. 13.7 - Prob. 13ECh. 13.7 - Prob. 14ECh. 13.7 - Prob. 15ECh. 13.7 - Prob. 16ECh. 13.7 - Finding an Equation of a Tangent Plane and a...Ch. 13.7 - Prob. 18ECh. 13.7 - Finding an Equation of a Tangent Plane and a...Ch. 13.7 - Prob. 20ECh. 13.7 - Prob. 21ECh. 13.7 - Finding an Equation of a Tangent Plane and a...Ch. 13.7 - Finding an Equation of a Tangent Plane and a...Ch. 13.7 - Prob. 24ECh. 13.7 - Prob. 25ECh. 13.7 - Prob. 26ECh. 13.7 - Prob. 27ECh. 13.7 - Prob. 28ECh. 13.7 - Finding the Equation of a Tangent Line to a Curve...Ch. 13.7 - Prob. 30ECh. 13.7 - Finding the Equation of a Tangent Line to a Curve...Ch. 13.7 - Prob. 32ECh. 13.7 - Prob. 33ECh. 13.7 - Prob. 34ECh. 13.7 - Finding the Angle of Inclination of a Tangent...Ch. 13.7 - Prob. 36ECh. 13.7 - Prob. 37ECh. 13.7 - Horizontal Tangent Plane In Exercises 37-42, find...Ch. 13.7 - Prob. 39ECh. 13.7 - Prob. 40ECh. 13.7 - Prob. 41ECh. 13.7 - Prob. 42ECh. 13.7 - Tangent Surfaces In Exercises 43 and 44, show that...Ch. 13.7 - Prob. 44ECh. 13.7 - Prob. 45ECh. 13.7 - Prob. 46ECh. 13.7 - Prob. 47ECh. 13.7 - Prob. 48ECh. 13.7 - Prob. 49ECh. 13.7 - Prob. 50ECh. 13.7 - Using an Ellipsoid Find a point on the ellipsoid...Ch. 13.7 - Prob. 52ECh. 13.7 - Prob. 53ECh. 13.7 - Prob. 54ECh. 13.7 - Prob. 55ECh. 13.7 - Prob. 56ECh. 13.7 - Prob. 57ECh. 13.7 - Prob. 58ECh. 13.7 - Prob. 59ECh. 13.7 - Tangent Planes Let f be a differentiable function...Ch. 13.7 - Prob. 61ECh. 13.7 - Approximation Repeat Exercise 61 for the function...Ch. 13.7 - Prob. 63ECh. 13.7 - Prob. 64ECh. 13.8 - CONCEPT CHECK Function of Two Variables For a...Ch. 13.8 - Prob. 2ECh. 13.8 - Prob. 3ECh. 13.8 - Prob. 4ECh. 13.8 - Prob. 5ECh. 13.8 - Prob. 6ECh. 13.8 - Prob. 7ECh. 13.8 - Prob. 8ECh. 13.8 - Prob. 9ECh. 13.8 - Prob. 10ECh. 13.8 - Prob. 11ECh. 13.8 - Prob. 12ECh. 13.8 - Prob. 13ECh. 13.8 - Prob. 14ECh. 13.8 - Prob. 15ECh. 13.8 - Prob. 16ECh. 13.8 - Prob. 17ECh. 13.8 - Prob. 18ECh. 13.8 - Prob. 19ECh. 13.8 - Prob. 20ECh. 13.8 - Prob. 21ECh. 13.8 - Prob. 22ECh. 13.8 - Prob. 23ECh. 13.8 - Prob. 24ECh. 13.8 - Prob. 25ECh. 13.8 - Prob. 26ECh. 13.8 - Prob. 27ECh. 13.8 - Prob. 28ECh. 13.8 - Prob. 29ECh. 13.8 - Prob. 30ECh. 13.8 - Prob. 31ECh. 13.8 - Prob. 32ECh. 13.8 - Prob. 33ECh. 13.8 - Prob. 34ECh. 13.8 - Prob. 35ECh. 13.8 - Prob. 36ECh. 13.8 - Prob. 37ECh. 13.8 - Prob. 38ECh. 13.8 - Prob. 39ECh. 13.8 - Prob. 40ECh. 13.8 - Prob. 41ECh. 13.8 - Prob. 42ECh. 13.8 - Prob. 43ECh. 13.8 - Finding Absolute Extrema In Exercises 39-46, find...Ch. 13.8 - Prob. 45ECh. 13.8 - Prob. 46ECh. 13.8 - Examining a Function In Exercises 47 and 48, find...Ch. 13.8 - Prob. 48ECh. 13.8 - Prob. 49ECh. 13.8 - Prob. 50ECh. 13.8 - Prob. 51ECh. 13.8 - Prob. 52ECh. 13.8 - Prob. 53ECh. 13.8 - Prob. 54ECh. 13.8 - True or False? In Exercises 55-58, determine...Ch. 13.8 - Prob. 56ECh. 13.8 - Prob. 57ECh. 13.8 - Prob. 58ECh. 13.9 - CONCEPT CHECK Applied Optimization Problems In...Ch. 13.9 - Prob. 2ECh. 13.9 - Prob. 3ECh. 13.9 - Prob. 4ECh. 13.9 - Prob. 5ECh. 13.9 - Prob. 6ECh. 13.9 - Prob. 7ECh. 13.9 - Prob. 8ECh. 13.9 - Finding Positive Numbers In Exercises 7-10, find...Ch. 13.9 - Finding Positive Numbers In Exercises 7-10, find...Ch. 13.9 - Cost A home improvement contractor is painting the...Ch. 13.9 - Maximum Volume The material for constructing the...Ch. 13.9 - Prob. 13ECh. 13.9 - Maximum Volume Show that the rectangular box of...Ch. 13.9 - Prob. 15ECh. 13.9 - Prob. 16ECh. 13.9 - Prob. 17ECh. 13.9 - Shannon Diversity Index One way to measure species...Ch. 13.9 - Minimum Cost A water line is to be built from...Ch. 13.9 - Area A trough with trapezoidal cross sections is...Ch. 13.9 - Prob. 21ECh. 13.9 - Prob. 22ECh. 13.9 - Prob. 23ECh. 13.9 - Prob. 24ECh. 13.9 - Prob. 25ECh. 13.9 - Finding the Least Squares Regression Line In...Ch. 13.9 - Prob. 27ECh. 13.9 - Prob. 28ECh. 13.9 - Prob. 29ECh. 13.9 - Prob. 30ECh. 13.9 - Prob. 31ECh. 13.9 - HOW DO YOU SEE IT? Match the regression equation...Ch. 13.9 - Prob. 33ECh. 13.9 - Prob. 34ECh. 13.9 - Prob. 35ECh. 13.9 - Prob. 36ECh. 13.9 - Prob. 37ECh. 13.9 - Prob. 38ECh. 13.9 - Prob. 39ECh. 13.9 - Prob. 40ECh. 13.9 - Prob. 41ECh. 13.10 - CONCEPT CHECK Constrained Optimization Problems...Ch. 13.10 - Prob. 2ECh. 13.10 - Prob. 3ECh. 13.10 - Prob. 4ECh. 13.10 - Prob. 5ECh. 13.10 - Prob. 6ECh. 13.10 - Using Lagrange Multipliers In Exercises 3-10. use...Ch. 13.10 - Prob. 8ECh. 13.10 - Prob. 9ECh. 13.10 - Prob. 10ECh. 13.10 - Prob. 11ECh. 13.10 - Prob. 12ECh. 13.10 - Prob. 13ECh. 13.10 - Prob. 14ECh. 13.10 - Prob. 15ECh. 13.10 - Prob. 16ECh. 13.10 - Prob. 17ECh. 13.10 - Prob. 18ECh. 13.10 - Prob. 19ECh. 13.10 - Prob. 20ECh. 13.10 - Prob. 21ECh. 13.10 - Prob. 22ECh. 13.10 - Prob. 23ECh. 13.10 - Prob. 24ECh. 13.10 - Prob. 25ECh. 13.10 - Finding Minimum Distance In Exercises 19-28, use...Ch. 13.10 - Prob. 27ECh. 13.10 - Prob. 28ECh. 13.10 - Prob. 29ECh. 13.10 - Prob. 30ECh. 13.10 - Using Lagrange Multipliers In Exercises 31-38, use...Ch. 13.10 - Prob. 32ECh. 13.10 - Prob. 33ECh. 13.10 - Prob. 34ECh. 13.10 - Using Lagrange Multipliers In Exercises 31-38, use...Ch. 13.10 - Prob. 36ECh. 13.10 - Prob. 37ECh. 13.10 - Prob. 38ECh. 13.10 - Prob. 39ECh. 13.10 - Prob. 40ECh. 13.10 - EXPLORING CONCEPTS Method of Lagrange Multipliers...Ch. 13.10 - Prob. 42ECh. 13.10 - Minimum Cost A cargo container (in the shape of a...Ch. 13.10 - Geometric and Arithmetic Means (a) Use Lagrange...Ch. 13.10 - Prob. 45ECh. 13.10 - Prob. 46ECh. 13.10 - Prob. 47ECh. 13.10 - Prob. 48ECh. 13.10 - Prob. 49ECh. 13.10 - Prob. 50ECh. 13.10 - Prob. 51ECh. 13.10 - Prob. 52ECh. 13.10 - A can buoy is to be made of three pieces, namely,...Ch. 13 - Evaluating a Function In Exercises 1 and 2,...Ch. 13 - Prob. 2RECh. 13 - Prob. 3RECh. 13 - Finding the Domain and Range of a Function In...Ch. 13 - Prob. 5RECh. 13 - Prob. 6RECh. 13 - Sketching a Contour Map In Exercises 7 and 8,...Ch. 13 - Prob. 8RECh. 13 - Prob. 9RECh. 13 - Prob. 10RECh. 13 - Prob. 11RECh. 13 - Prob. 12RECh. 13 - Prob. 13RECh. 13 - Prob. 14RECh. 13 - Prob. 15RECh. 13 - Prob. 16RECh. 13 - Prob. 17RECh. 13 - Prob. 18RECh. 13 - Prob. 19RECh. 13 - Prob. 20RECh. 13 - Prob. 21RECh. 13 - Prob. 22RECh. 13 - Prob. 23RECh. 13 - Prob. 24RECh. 13 - Prob. 25RECh. 13 - Prob. 26RECh. 13 - Prob. 27RECh. 13 - Prob. 28RECh. 13 - Prob. 29RECh. 13 - Prob. 30RECh. 13 - Prob. 31RECh. 13 - Prob. 32RECh. 13 - Prob. 33RECh. 13 - Prob. 34RECh. 13 - Finding the Slopes of a Surface Find the slopes of...Ch. 13 - Prob. 36RECh. 13 - Prob. 37RECh. 13 - Prob. 38RECh. 13 - Prob. 39RECh. 13 - Prob. 40RECh. 13 - Using a Differential as an Approximation In...Ch. 13 - Prob. 42RECh. 13 - Volume The possible error involved in measuring...Ch. 13 - Prob. 44RECh. 13 - Prob. 45RECh. 13 - Prob. 46RECh. 13 - Prob. 47RECh. 13 - Prob. 48RECh. 13 - Using Different Methods In Exercises 47-50, find...Ch. 13 - Prob. 50RECh. 13 - Prob. 51RECh. 13 - Prob. 52RECh. 13 - Prob. 53RECh. 13 - Prob. 54RECh. 13 - Prob. 55RECh. 13 - Prob. 56RECh. 13 - Prob. 57RECh. 13 - Prob. 58RECh. 13 - Prob. 59RECh. 13 - Prob. 60RECh. 13 - Prob. 61RECh. 13 - Prob. 62RECh. 13 - Prob. 63RECh. 13 - Prob. 64RECh. 13 - Prob. 65RECh. 13 - Using Properties of the Gradient In Exercises...Ch. 13 - Prob. 67RECh. 13 - Prob. 68RECh. 13 - Prob. 69RECh. 13 - Prob. 70RECh. 13 - Prob. 71RECh. 13 - Prob. 72RECh. 13 - Prob. 73RECh. 13 - Prob. 74RECh. 13 - Finding the Angle of Inclination of a Tangent...Ch. 13 - Prob. 76RECh. 13 - Prob. 77RECh. 13 - Prob. 78RECh. 13 - Prob. 79RECh. 13 - Prob. 80RECh. 13 - Prob. 81RECh. 13 - Prob. 82RECh. 13 - Prob. 83RECh. 13 - Prob. 84RECh. 13 - Prob. 85RECh. 13 - Prob. 86RECh. 13 - Prob. 87RECh. 13 - Prob. 88RECh. 13 - Finding the Least Squares Regression Line In...Ch. 13 - Prob. 90RECh. 13 - Prob. 91RECh. 13 - Prob. 92RECh. 13 - Prob. 93RECh. 13 - Using Lagrange Multipliers In Exercises 93-98, use...Ch. 13 - Prob. 95RECh. 13 - Prob. 96RECh. 13 - Prob. 97RECh. 13 - Prob. 98RECh. 13 - Minimum Cost A water line is to be built from...Ch. 13 - Area Herons Formula states that the area of a...Ch. 13 - Minimizing Material An industrial container is in...Ch. 13 - Tangent Plane Let P(x0,y0,z0) be a point in the...Ch. 13 - Prob. 4PSCh. 13 - Prob. 5PSCh. 13 - Minimizing Costs A heated storage room has the...Ch. 13 - Prob. 7PSCh. 13 - Temperature Consider a circular plate of radius 1...Ch. 13 - Prob. 9PSCh. 13 - Minimizing Area Consider the ellipse x2a2+y2b2=1...Ch. 13 - Prob. 11PSCh. 13 - Prob. 12PSCh. 13 - Prob. 13PSCh. 13 - Prob. 14PSCh. 13 - Prob. 15PSCh. 13 - Tangent Planes Let f be a differentiable function...Ch. 13 - Prob. 17PSCh. 13 - Prob. 18PSCh. 13 - Prob. 19PSCh. 13 - Prob. 20PSCh. 13 - Prob. 21PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 7. Let F(x1, x2) (F₁(x1, x2), F2(x1, x2)), where = X2 F1(x1, x2) X1 F2(x1, x2) x+x (i) Using the definition, calculate the integral LF.dy, where (t) = (cos(t), sin(t)) and t = [0,2]. [5 Marks] (ii) Explain why Green's Theorem cannot be used to find the integral in part (i). [5 Marks]arrow_forward6. Sketch the trace of the following curve on R², п 3п (t) = (t2 sin(t), t2 cos(t)), tЄ 22 [3 Marks] Find the length of this curve. [7 Marks]arrow_forwardTotal marks 10 Total marks on naner: 80 7. Let DCR2 be a bounded domain with the boundary OD which can be represented as a smooth closed curve : [a, b] R2, oriented in the anticlock- wise direction. Use Green's Theorem to justify that the area of the domain D can be computed by the formula 1 Area(D) = ½ (−y, x) · dy. [5 Marks] (ii) Use the area formula in (i) to find the area of the domain D enclosed by the ellipse y(t) = (10 cos(t), 5 sin(t)), t = [0,2π]. [5 Marks]arrow_forward
- Total marks 15 Total marks on paper: 80 6. Let DCR2 be a bounded domain with the boundary ǝD which can be represented as a smooth closed curve : [a, b] → R², oriented in the anticlockwise direction. (i) Use Green's Theorem to justify that the area of the domain D can be computed by the formula 1 Area(D) = . [5 Marks] (ii) Use the area formula in (i) to find the area of the domain D enclosed by the ellipse (t) = (5 cos(t), 10 sin(t)), t = [0,2π]. [5 Marks] (iii) Explain in your own words why Green's Theorem can not be applied to the vector field У x F(x,y) = ( - x² + y²²x² + y² ). [5 Marks]arrow_forwardTotal marks 15 པ་ (i) Sketch the trace of the following curve on R2, (t) = (t2 cos(t), t² sin(t)), t = [0,2π]. [3 Marks] (ii) Find the length of this curve. (iii) [7 Marks] Give a parametric representation of a curve : [0, that has initial point (1,0), final point (0, 1) and the length √2. → R² [5 Marks] Turn over. MA-201: Page 4 of 5arrow_forwardTotal marks 15 5. (i) Let f R2 R be defined by f(x1, x2) = x² - 4x1x2 + 2x3. Find all local minima of f on R². (ii) [10 Marks] Give an example of a function f: R2 R which is not bounded above and has exactly one critical point, which is a minimum. Justify briefly your answer. [5 Marks] 6. (i) Sketch the trace of the following curve on R2, y(t) = (sin(t), 3 sin(t)), t = [0,π]. [3 Marks]arrow_forward
- A ladder 25 feet long is leaning against the wall of a building. Initially, the foot of the ladder is 7 feet from the wall. The foot of the ladder begins to slide at a rate of 2 ft/sec, causing the top of the ladder to slide down the wall. The location of the foot of the ladder, its x coordinate, at time t seconds is given by x(t)=7+2t. wall y(1) 25 ft. ladder x(1) ground (a) Find the formula for the location of the top of the ladder, the y coordinate, as a function of time t. The formula for y(t)= √ 25² - (7+2t)² (b) The domain of t values for y(t) ranges from 0 (c) Calculate the average velocity of the top of the ladder on each of these time intervals (correct to three decimal places): . (Put your cursor in the box, click and a palette will come up to help you enter your symbolic answer.) time interval ave velocity [0,2] -0.766 [6,8] -3.225 time interval ave velocity -1.224 -9.798 [2,4] [8,9] (d) Find a time interval [a,9] so that the average velocity of the top of the ladder on this…arrow_forwardTotal marks 15 3. (i) Let FRN Rm be a mapping and x = RN is a given point. Which of the following statements are true? Construct counterex- amples for any that are false. (a) If F is continuous at x then F is differentiable at x. (b) If F is differentiable at x then F is continuous at x. If F is differentiable at x then F has all 1st order partial (c) derivatives at x. (d) If all 1st order partial derivatives of F exist and are con- tinuous on RN then F is differentiable at x. [5 Marks] (ii) Let mappings F= (F1, F2) R³ → R² and G=(G1, G2) R² → R² : be defined by F₁ (x1, x2, x3) = x1 + x², G1(1, 2) = 31, F2(x1, x2, x3) = x² + x3, G2(1, 2)=sin(1+ y2). By using the chain rule, calculate the Jacobian matrix of the mapping GoF R3 R², i.e., JGoF(x1, x2, x3). What is JGOF(0, 0, 0)? (iii) [7 Marks] Give reasons why the mapping Go F is differentiable at (0, 0, 0) R³ and determine the derivative matrix D(GF)(0, 0, 0). [3 Marks]arrow_forward5. (i) Let f R2 R be defined by f(x1, x2) = x² - 4x1x2 + 2x3. Find all local minima of f on R². (ii) [10 Marks] Give an example of a function f: R2 R which is not bounded above and has exactly one critical point, which is a minimum. Justify briefly Total marks 15 your answer. [5 Marks]arrow_forward
- Total marks 15 4. : Let f R2 R be defined by f(x1, x2) = 2x²- 8x1x2+4x+2. Find all local minima of f on R². [10 Marks] (ii) Give an example of a function f R2 R which is neither bounded below nor bounded above, and has no critical point. Justify briefly your answer. [5 Marks]arrow_forward4. Let F RNR be a mapping. (i) x ЄRN ? (ii) : What does it mean to say that F is differentiable at a point [1 Mark] In Theorem 5.4 in the Lecture Notes we proved that if F is differentiable at a point x E RN then F is continuous at x. Proof. Let (n) CRN be a sequence such that xn → x ЄERN as n → ∞. We want to show that F(xn) F(x), which means F is continuous at x. Denote hnxn - x, so that ||hn|| 0. Thus we find ||F(xn) − F(x)|| = ||F(x + hn) − F(x)|| * ||DF (x)hn + R(hn) || (**) ||DF(x)hn||+||R(hn)||| → 0, because the linear mapping DF(x) is continuous and for all large nЄ N, (***) ||R(hn) || ||R(hn) || ≤ → 0. ||hn|| (a) Explain in details why ||hn|| → 0. [3 Marks] (b) Explain the steps labelled (*), (**), (***). [6 Marks]arrow_forward4. In Theorem 5.4 in the Lecture Notes we proved that if F: RN → Rm is differentiable at x = RN then F is continuous at x. Proof. Let (xn) CRN be a sequence such that x → x Є RN as n → ∞. We want F(x), which means F is continuous at x. to show that F(xn) Denote hn xnx, so that ||hn||| 0. Thus we find ||F (xn) − F(x) || (*) ||F(x + hn) − F(x)|| = ||DF(x)hn + R(hn)|| (**) ||DF(x)hn|| + ||R(hn) || → 0, because the linear mapping DF(x) is continuous and for all large n = N, |||R(hn) || ≤ (***) ||R(hn)|| ||hn|| → 0. Explain the steps labelled (*), (**), (***) [6 Marks] (ii) Give an example of a function F: RR such that F is contin- Total marks 10 uous at x=0 but F is not differentiable at at x = 0. [4 Marks]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY