Elementary Technical Mathematics
11th Edition
ISBN: 9781285199191
Author: Dale Ewen, C. Robert Nelson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 13.1, Problem 11E
Use right triangle ABC in Illustration 1 and the Pythagorean theorem to find each unknown side, rounded to three significant digits:
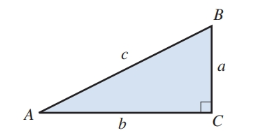
ILLUSTRATION 1
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
18:36
G.C.A.2.ChordsSecantsandTa...
จ 76
完成
2 In the accompanying diagram, AABC is inscribed
in circle O, AP bisects BAC, PBD is tangent to
circle O at B, and
mZACB:m/CAB:m/ABC= 4:3:2
D
B
P
F
Find: mZABC, mBF, m/BEP, m/P, m/PBC
←
1
Ő
14:09
2/16
jmap.org
5G 66
In the accompanying diagram of circle O,
diameters BD and AE, secants PAB and PDC, and
chords BC and AD are drawn; mAD = 40; and
mDC
= 80.
B
E
Find: mAB, m/BCD, m/BOE, m/P, m/PAD
←
G.C.A.2.ChordsSecantsand Tangent
s19.pdf (538 KB)
+
4
保存... X
16:39
<
文字
15:28
|美图秀秀
保存
59%
5G 46
照片
完成
Bonvicino - Period
Name:
6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner
that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A
wedge (from the center) is then removed from this solid as shown in Diagram 3.
30
Diogram 1
Diegrom 2.
Diagram 3.
If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of
the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the
exact volume of the solid in Diagram 3, measured in cubic meters. Show all work.
(T
文字
贴纸
消除笔
涂鸦笔
边框
马赛克
去美容
Chapter 13 Solutions
Elementary Technical Mathematics
Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 5ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 7ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 9ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...
Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 13ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 15ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 17ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 20ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 23ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 27ECh. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 29ECh. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 31ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 33ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 37ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 41ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 43ECh. 13.1 - Prob. 44ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 46ECh. 13.1 - Prob. 47ECh. 13.1 - Prob. 48ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 51ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 53ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 55ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 57ECh. 13.1 - Prob. 58ECh. 13.1 - Prob. 59ECh. 13.1 - Prob. 60ECh. 13.1 - Prob. 61ECh. 13.1 - Prob. 62ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 64ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 66ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 68ECh. 13.1 - Prob. 69ECh. 13.1 - Prob. 70ECh. 13.1 - Prob. 71ECh. 13.1 - Prob. 72ECh. 13.1 - Prob. 73ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 5ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 7ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 9ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 17ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 19ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 21ECh. 13.2 - Prob. 22ECh. 13.2 - Prob. 23ECh. 13.2 - Prob. 24ECh. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Prob. 11ECh. 13.3 - Prob. 12ECh. 13.3 - Prob. 13ECh. 13.3 - Prob. 14ECh. 13.3 - Prob. 15ECh. 13.3 - Prob. 16ECh. 13.3 - Prob. 17ECh. 13.3 - Prob. 18ECh. 13.3 - Prob. 19ECh. 13.3 - Prob. 20ECh. 13.3 - Prob. 21ECh. 13.3 - Prob. 22ECh. 13.3 - Prob. 23ECh. 13.3 - Prob. 24ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 3ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 9ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 11ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 13ECh. 13.4 - Prob. 14ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 16ECh. 13.4 - Prob. 17ECh. 13.4 - Prob. 18ECh. 13.4 - Prob. 19ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 21ECh. 13.4 - Prob. 22ECh. 13.4 - Prob. 23ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.5 - A conveyor is used to lift paper to a shredder....Ch. 13.5 - A bullet is found embedded in the wall of a room...Ch. 13.5 - The recommended safety angle of a ladder against a...Ch. 13.5 - A piece of conduit 38.0 ft long is placed across...Ch. 13.5 - Find the width of the river in Illustration 4....Ch. 13.5 - Prob. 7ECh. 13.5 - A smokestack is 180 ft high. A guy wire must be...Ch. 13.5 - A railroad track has an angle of elevation of 1.0....Ch. 13.5 - Prob. 10ECh. 13.5 - Enrico has to draft a triangular roof to a house....Ch. 13.5 - A small plane takes off from an airport and begins...Ch. 13.5 - A gauge is used to check the diameter of a crank-...Ch. 13.5 - Round metal duct runs alongside some stairs from...Ch. 13.5 - The cables attached to a TV relay tower are 110 m...Ch. 13.5 - Prob. 16ECh. 13.5 - Prob. 17ECh. 13.5 - Prob. 18ECh. 13.5 - Use the right triangle in Illustration 13: a. Find...Ch. 13.5 - Prob. 20ECh. 13.5 - Twelve equally spaced holes must be drilled on a...Ch. 13.5 - Dimension x in the dovetail shown in Illustration...Ch. 13.5 - Find angle of the taper in Illustration 17....Ch. 13.5 - You need to use a metal screw with a head angle of...Ch. 13.5 - Prob. 25ECh. 13.5 - Prob. 26ECh. 13.5 - Find length x and angle A in Illustration 21....Ch. 13.5 - From the base of a building, measure out a...Ch. 13.5 - A mechanical draftsperson needs to find the...Ch. 13.5 - Prob. 30ECh. 13.5 - Prob. 31ECh. 13.5 - Prob. 32ECh. 13.5 - Solar heating and electric panels should face the...Ch. 13.5 - A lean-to is a simple shelter with three walls, a...Ch. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - Prob. 3RCh. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - Prob. 5RCh. 13 - Prob. 6RCh. 13 - Prob. 7RCh. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find angle A in Illustration 2. ILLUSTRATION 2Ch. 13 - Find angle B in Illustration 2. ILLUSTRATION 2Ch. 13 - Find side b in Illustration3. ILLUSTRATION 3Ch. 13 - Prob. 17RCh. 13 - Prob. 18RCh. 13 - Solve each right triangle:Ch. 13 - Prob. 20RCh. 13 - A satellite is directly overhead one observer...Ch. 13 - A ranger at the top of a fire tower observes the...Ch. 13 - Find the angle of slope of the symmetrical roof in...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find angle B Illustration 1. ILLUSTRATION 1Ch. 13 - Find side a Illustration 1. ILLUSTRATION 1Ch. 13 - Find side c Illustration 1. ILLUSTRATION 1Ch. 13 - Find angle A Illustration 2. ILLUSTRATION 2Ch. 13 - Find angle B Illustration 2. ILLUSTRATION 2Ch. 13 - Find side b Illustration 2. ILLUSTRATION 2Ch. 13 - A tower 50.0 ft high has a guy wire that is...Ch. 13 - Find length x in the retaining wall in...Ch. 13 - Find angle A in the retaining wall in Illustration...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Answer question 4 pleasearrow_forward16:39 < 文字 15:28 |美图秀秀 保存 59% 5G 46 照片 完成 Bonvicino - Period Name: 6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A wedge (from the center) is then removed from this solid as shown in Diagram 3. 30 Diogram 1 Diegrom 2. Diagram 3. If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the exact volume of the solid in Diagram 3, measured in cubic meters. Show all work. (T 文字 贴纸 消除笔 涂鸦笔 边框 马赛克 去美容arrow_forwardAnswer question 3 pleasearrow_forward
- Answer question 3 pleasearrow_forward38 Below triangle is isosceles. Find the value of x. 70° 60° x 20° Warrow_forwardProblem 11 (a) A tank is discharging water through an orifice at a depth of T meter below the surface of the water whose area is A m². The following are the values of a for the corresponding values of A: A 1.257 1.390 x 1.50 1.65 1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650 1.80 1.95 2.10 2.25 2.40 2.55 2.70 2.85 Using the formula -3.0 (0.018)T = dx. calculate T, the time in seconds for the level of the water to drop from 3.0 m to 1.5 m above the orifice. (b) The velocity of a train which starts from rest is given by the fol- lowing table, the time being reckoned in minutes from the start and the speed in km/hour: | † (minutes) |2|4 6 8 10 12 14 16 18 20 v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0 Estimate approximately the total distance ran in 20 minutes.arrow_forward
- - Let n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p − 1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., p-1 2 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). 23 32 how come? The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. The set T is the subset of these residues exceeding So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1.arrow_forwardLet n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p-1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., 2 p-1 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. 23 The set T is the subset of these residues exceeding 2° So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1. how come?arrow_forwardShading a Venn diagram with 3 sets: Unions, intersections, and... The Venn diagram shows sets A, B, C, and the universal set U. Shade (CUA)' n B on the Venn diagram. U Explanation Check A- B Q Search 田arrow_forward
- 3. A different 7-Eleven has a bank of slurpee fountain heads. Their available flavors are as follows: Mountain Dew, Mountain Dew Code Red, Grape, Pepsi and Mountain Dew Livewire. You fill five different cups full with each type of flavor. How many different ways can you arrange the cups in a line if exactly two Mountain Dew flavors are next to each other? 3.2.1arrow_forwardBusinessarrow_forwardWhat is the area of this figure? 5 mm 4 mm 3 mm square millimeters 11 mm Submit 8 mm Work it out 9 mmarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License