
Let’s look in more detail at how a satellite is moved from one circular orbit to another. FIGURE CPI3.71 shows two orbits, of radii r1 and r2 and an elliptical orbit that connects them. Points 1 and 2 are at the ends of the semimajor axis of the ellipse.
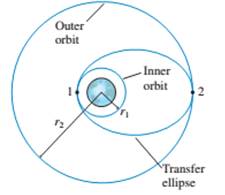
FIGURE CPI3.71
a. A satellite moving along the elliptical orbit has to satisfy two conservation laws. Use these two laws to prove that the velocities at point 1 and 2 are
The prime indicates that these are the velocities on the elliptical orbit. Both reduce to Equation 13.22 if r1 =r2 = r.
b. Consider a 1000 kg communications satellite that needs to be boosted from an orbit 300 km above the earth to a geosynchronous orbit 35,900 km above the earth. Find the velocity v1on the inner circular orbit and the velocity
c. How much work must the rocket motor do to transfer the satellite from the circular orbit to the elliptical orbit?
d. Now find the velocity
e. How much work must the rocket motor do to transfer the satellite from the elliptical orbit to the outer circular orbit?
f. Compute the total work done and compare your answer to the result of Example 13.6.
Want to see the full answer?
Check out a sample textbook solution
Chapter 13 Solutions
Physics for Scientists and Engineers: A Strategic Approach with Modern Physics, Books a la Carte Edition; Student Workbook for Physics for Scientists ... eText -- ValuePack Access Card (4th Edition)
- Children playing in a playground on the flat roof of a city school lose their ball to the parking lot below. One of the teachers kicks the ball back up to the children as shown in the figure below. The playground is 6.10 m above the parking lot, and the school building's vertical wall is h = 7.40 m high, forming a 1.30 m high railing around the playground. The ball is launched at an angle of 8 = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. (Due to the nature of this problem, do not use rounded intermediate values-including answers submitted in WebAssign-in your calculations.) (a) Find the speed (in m/s) at which the ball was launched. 18.1 m/s (b) Find the vertical distance (in m) by which the ball clears the wall. 0.73 ✓ m (c) Find the horizontal distance (in m) from the wall to the point on the roof where the ball lands. 2.68 m (d) What If? If the teacher always launches the ball…arrow_forwardIt is not possible to see very small objects, such as viruses, using an ordinary light microscope. An electron microscope can view such objects using an electron beam instead of a light beam. Electron microscopy has proved invaluable for investigations of viruses, cell membranes and subcellular structures, bacterial surfaces, visual receptors, chloroplasts, and the contractile properties of muscles. The "lenses" of an electron microscope consist of electric and magnetic fields that control the electron beam. As an example of the manipulation of an electron beam, consider an electron traveling away from the origin along the x axis in the xy plane with initial velocity ₁ = vi. As it passes through the region x = 0 to x=d, the electron experiences acceleration a = ai +a, where a and a, are constants. For the case v, = 1.67 x 107 m/s, ax = 8.51 x 1014 m/s², and a = 1.50 x 10¹5 m/s², determine the following at x = d = 0.0100 m. (a) the position of the electron y, = 2.60e1014 m (b) the…arrow_forwardNo chatgpt plsarrow_forward
- need help with the first partarrow_forwardA ball is thrown with an initial speed v, at an angle 6, with the horizontal. The horizontal range of the ball is R, and the ball reaches a maximum height R/4. In terms of R and g, find the following. (a) the time interval during which the ball is in motion 2R (b) the ball's speed at the peak of its path v= Rg 2 √ sin 26, V 3 (c) the initial vertical component of its velocity Rg sin ei sin 20 (d) its initial speed Rg √ sin 20 × (e) the angle 6, expressed in terms of arctan of a fraction. 1 (f) Suppose the ball is thrown at the same initial speed found in (d) but at the angle appropriate for reaching the greatest height that it can. Find this height. hmax R2 (g) Suppose the ball is thrown at the same initial speed but at the angle for greatest possible range. Find this maximum horizontal range. Xmax R√3 2arrow_forwardAn outfielder throws a baseball to his catcher in an attempt to throw out a runner at home plate. The ball bounces once before reaching the catcher. Assume the angle at which the bounced ball leaves the ground is the same as the angle at which the outfielder threw it as shown in the figure, but that the ball's speed after the bounce is one-half of what it was before the bounce. 8 (a) Assuming the ball is always thrown with the same initial speed, at what angle & should the fielder throw the ball to make it go the same distance D with one bounce (blue path) as a ball thrown upward at 35.0° with no bounce (green path)? 24 (b) Determine the ratio of the time interval for the one-bounce throw to the flight time for the no-bounce throw. Cone-bounce no-bounce 0.940arrow_forward
- A rocket is launched at an angle of 60.0° above the horizontal with an initial speed of 97 m/s. The rocket moves for 3.00 s along its initial line of motion with an acceleration of 28.0 m/s². At this time, its engines fail and the rocket proceeds to move as a projectile. (a) Find the maximum altitude reached by the rocket. 1445.46 Your response differs from the correct answer by more than 10%. Double check your calculations. m (b) Find its total time of flight. 36.16 x Your response is within 10% of the correct value. This may be due to roundoff error, or you could have a mistake in your calculation. Carry out all intermediate results to at least four-digit accuracy to minimize roundoff error. s (c) Find its horizontal range. 1753.12 × Your response differs from the correct answer by more than 10%. Double check your calculations. marrow_forwardRace car driver is cruising down the street at a constant speed of 28.9 m/s (~65 mph; he has a “lead” foot) when the traffic light in front of him turns red. a) If the driver’s reaction time is 160 ms, how far does he and his car travel down the road from the instant he sees the light change to the instant he begins to slow down? b) If the driver’s combined reaction and movement time is 750 ms, how far do he and his car travel down the road from the instant he sees the light change to the instant he slams on her brakes and car begins to slow down? Please answer parts a-B. Show all work. For each question draw a diagram to show the vector/s. Show all the step and provide units in the answers. Provide answer to 2 decimal places. DONT FORGET TO DRAW VECTORS! ONLY USE BASIC FORMULAS TAUGHT IN PHYSICS. distance = speed * time.arrow_forwardRace car driver is cruising down the street at a constant speed of 28.9 m/s (~65 mph; he has a “lead” foot) when the traffic light in front of him turns red. a) If the driver’s reaction time is 160 ms, how far does he and his car travel down the road from the instant he sees the light change to the instant he begins to slow down? b) If the driver’s combined reaction and movement time is 750 ms, how far do he and his car travel down the road from the instant he sees the light change to the instant he slams on her brakes and car begins to slow down? c) If the driver’s average rate of acceleration is -9.5 m/s2 as he slows down, how long does it take him to come to a stop (use information about his speed of 28.9 m/s but do NOT use his reaction and movement time in this computation)? Please answer parts a-c. Show all work. For each question draw a diagram to show the vector/s. Show all the step and provide units in the answers. Provide answer to 2 decimal places unless stated otherwise.…arrow_forward
- How is it that part a is connected to part b? I can't seem to solve either part and don't see the connection between the two.arrow_forwardHello, please help with inputing trial one into the equation, I just need a model for the first one so I can answer the rest. Also, does my data have the correct sigfig? Thanks!arrow_forwardFind the current in the R₁ resistor in the drawing (V₁=16.0V, V2=23.0 V, V₂ = 16.0V, R₁ = 2005, R₂ = and R₂ = 2.705) 2.3052 VIT A www R www R₂ R₂ Vaarrow_forward
 Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





