
Concept explainers
a.
Identify and explain whichof the given modelscan be recommended.
a.
Answer to Problem 66SE
The model with 2 predictors and the model with 3 predictors can be recommended for predicting the pH before addition of dyes.
Explanation of Solution
Given info:
The MINITAB output shows the best regression option for the data predicted for pH before the addition of dyes using carpet density, carpet weight, dye weight, dye weight as a percentage of carpet and pH after addition of dyes.
Justification:
Mallows
It is used to assess the fit of regression model where the aim to find the best subset of predictors. A relatively small value of
By observing the mallows
By examining the models with three variables,
Hence, the model with two predictorsnamely dye weight and pH after addition of dyes could be considered as a best model subset for predicting pH before the addition of dyes.
Also, a second option would be the model with three predictorsnamely carpet weight, dye weight and pH after addition of dyes could be considered as a best model subset for predicting pH before the addition of dyes.
b.
Test whether the model suggests a useful linear relationship between pH before the addition of dyes and at least one of the predictors.
b.
Answer to Problem 66SE
There is sufficient evidence to conclude that the there is a use of linear relationship between pH before the addition of dyes and at least one of the predictors dye weight and pH after the addition of dyes.
Explanation of Solution
Given info:
The MINITAB output for predicting the pH before the addition of dyes using the dye weight
Calculation:
The test hypotheses are given below:
Null hypothesis:
That is, there is no use of linear relationship between pH before the addition of dyes and the predictors dye weightand pH after the addition of dyes.
Alternative hypothesis:
That is, there is a use of linear relationship between pH before the addition of dyes and at least one of the predictors dye weightand pH after the addition of dyes.
Conclusion:
The P-value is 0.000 and the level of significance is 0.001.
The P-value is lesser than the level of significance.
That is
Thus, the null hypothesis is rejected.
Hence, there is sufficient evidence to conclude that there is a use of linear relationship between pH before the addition of dyes and at least one of the predictors dye weight and pH after the addition of dyes.
c.
Explain whether either one of the predictors could be eliminated from the model given that the other predictor is retained.
c.
Answer to Problem 66SE
No, either one of the predictors could not be eliminated from the model given that the other predictor is retained.
Explanation of Solution
Calculation:
For variable
Testing the hypothesis:
Null hypothesis:
That is, there is no use of linear relationship between pH before the addition of dyes and dye weightgiven that pH after addition of dyes was retained in the model.
Alternative hypothesis:
That is, there is a use of linear relationship between pH before the addition of dyes and dye weightgiven that pH after addition of dyes was retained in the model.
From the MINITAB output it can be observed that the P-value corresponding to the t statistic of
Conclusion:
The P-value is 0.000 and the level of significance is 0.001.
The P-value is lesser than the level of significance.
That is
Thus, the null hypothesis is rejected.
Hence, there is sufficient evidence to conclude that there is a use of linear relationship between pH before the addition of dyes and dye weight given that pH after addition of dyes was retained in the model.
For variable
Testing the hypothesis:
Null hypothesis:
That is, there is no use of linear relationship between pH before the addition of dyes and pH after addition of dyes given that dye weight was retained in the model.
Alternative hypothesis:
That is, there is a use of linear relationship between pH before the addition of dyes and pH after addition of dyes given that dye weight was retained in the model.
From the MINITAB output it can be observed that the P-value corresponding to the t statistic of
Conclusion:
The P-value is 0.000 and the level of significance is 0.001.
The P-value is lesser than the level of significance.
That is
Thus, the null hypothesis is rejected.
Hence, there is sufficient evidence to conclude that there is a use of linear relationship between pH before the addition of dyes and pH after addition of dyes given that dye weight was retained in the model.
Justification:
From the analysis it can be concluded that none of the variables can be eliminated from the model given that the other variable is already present in the model.
d.
Calculate and interpret the 95% confidence interval for the two predictors.
d.
Answer to Problem 66SE
The 95% confidence interval for the estimated slope coefficient
(–0.0000684, –0.0000244).
The 95% confidence interval for the estimated slope coefficient
Explanation of Solution
Calculation:
The 95% confidence interval is calculated using the formula:
The confidence interval is calculated using the formula:
Where,
n is the total number of observations.
k is the total number of predictors in the model.
Critical value:
Software procedure:
Step-by-step procedure to find the critical value is given below:
- Click on Graph, select View Probability and click OK.
- Select t, enter 111 as Degrees of freedom, inShaded Area Tab select Probability under Define Shaded Area By and choose Both tails.
- Enter Probability value as 0.05.
- Click OK.
Output obtained from MINITAB is given below:
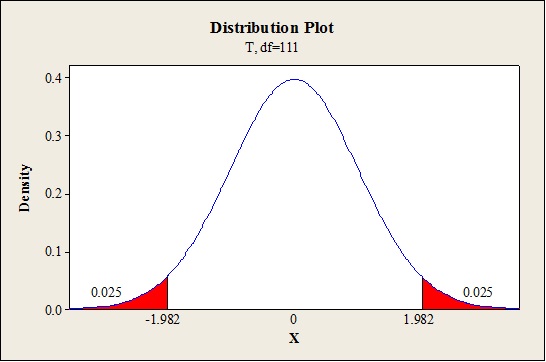
The 95% confidence interval for
Thus, the 95% confidence interval for the estimated slope coefficient
(–0.0000684, –0.0000244).
The 95% confidence interval for
Thus, the 95% confidence interval for the estimated slope coefficient
(0.6417,0.8325).
Interpretation:
For the variable
For one unit increase in the dye weight, it is 95% confident that the estimated value of pH before addition of dyes would decrease between–0.00000684 and–0.0000244 given that pH after addition of dyes is fixed constant.
For the variable
For one unit increase in the pH after the addition of dyes it is 95% confident that the estimated value of pH before addition of dyes would increase between 0.6417 and 0.8325 given that dye weight is fixed constant.
e.
Calculate and interpret the 95% confidence interval for the average value of pH before the addition of dyes when the dye weight and pH after the addition of dyes takes 1,000 and 6, respectively.
e.
Answer to Problem 66SE
The 95% confidence interval for the average value of pH before the addition of dyes when the dye weight and pH after the addition of dyes takes 1,000 and 6, respectively is (5.250, 5.383)
Explanation of Solution
Given info:
The estimated standard deviation for predicting the pH before the addition of dyes when the dye weight and pH after the addition of dyes takes 1,000 and 6 is 0.0336.
Calculation:
The average value of pH before the addition of dyes when the dye weight and pH after the addition of dyes takes 1,000 and 6 is calculated as follows:
Thus, the average value of pH before the addition of dyes when the dye weight and pH after the addition of dyes takes 1,000 and 6 is 5.316.
95% confidence interval for the true response:
The confidence interval is calculated using the formula:
Where,
n is the total number of observations.
k is the total number of predictors in the model.
Critical value:
Software procedure:
Step-by-step procedure to find the critical value is given below:
- Click on Graph, select View Probability and click OK.
- Select t, enter 111 as Degrees of freedom, in Shaded Area Tab select Probability under Define Shaded Area By and choose Both tails.
- Enter Probability value as 0.05.
- Click OK.
Output obtained from MINITAB is given below:

The 95% confidence interval is given below:
Thus, the 95% confidence interval for the average value of pH before the addition of dyes when the dye weight and pH after the addition of dyes takes 1,000 and 6 is (5.250,5.383).
Interpretation:
It is 95% confident that average value of pH before the addition of dyes when the dye weight and pH after the addition of dyes takes 1,000 and 6 would lie between 5.250 and 5.383.
Want to see more full solutions like this?
Chapter 13 Solutions
Probability and Statistics for Engineering and the Sciences
- Find the following probability P(z<-.24)arrow_forward3. Explain why the following statements are not correct. a. "With my methodological approach, I can reduce the Type I error with the given sample information without changing the Type II error." b. "I have already decided how much of the Type I error I am going to allow. A bigger sample will not change either the Type I or Type II error." C. "I can reduce the Type II error by making it difficult to reject the null hypothesis." d. "By making it easy to reject the null hypothesis, I am reducing the Type I error."arrow_forwardGiven the following sample data values: 7, 12, 15, 9, 15, 13, 12, 10, 18,12 Find the following: a) Σ x= b) x² = c) x = n d) Median = e) Midrange x = (Enter a whole number) (Enter a whole number) (use one decimal place accuracy) (use one decimal place accuracy) (use one decimal place accuracy) f) the range= g) the variance, s² (Enter a whole number) f) Standard Deviation, s = (use one decimal place accuracy) Use the formula s² ·Σx² -(x)² n(n-1) nΣ x²-(x)² 2 Use the formula s = n(n-1) (use one decimal place accuracy)arrow_forward
- Table of hours of television watched per week: 11 15 24 34 36 22 20 30 12 32 24 36 42 36 42 26 37 39 48 35 26 29 27 81276 40 54 47 KARKE 31 35 42 75 35 46 36 42 65 28 54 65 28 23 28 23669 34 43 35 36 16 19 19 28212 Using the data above, construct a frequency table according the following classes: Number of Hours Frequency Relative Frequency 10-19 20-29 |30-39 40-49 50-59 60-69 70-79 80-89 From the frequency table above, find a) the lower class limits b) the upper class limits c) the class width d) the class boundaries Statistics 300 Frequency Tables and Pictures of Data, page 2 Using your frequency table, construct a frequency and a relative frequency histogram labeling both axes.arrow_forwardTable of hours of television watched per week: 11 15 24 34 36 22 20 30 12 32 24 36 42 36 42 26 37 39 48 35 26 29 27 81276 40 54 47 KARKE 31 35 42 75 35 46 36 42 65 28 54 65 28 23 28 23669 34 43 35 36 16 19 19 28212 Using the data above, construct a frequency table according the following classes: Number of Hours Frequency Relative Frequency 10-19 20-29 |30-39 40-49 50-59 60-69 70-79 80-89 From the frequency table above, find a) the lower class limits b) the upper class limits c) the class width d) the class boundaries Statistics 300 Frequency Tables and Pictures of Data, page 2 Using your frequency table, construct a frequency and a relative frequency histogram labeling both axes.arrow_forwardA study was undertaken to compare respiratory responses of hypnotized and unhypnotized subjects. The following data represent total ventilation measured in liters of air per minute per square meter of body area for two independent (and randomly chosen) samples. Analyze these data using the appropriate non-parametric hypothesis test. Unhypnotized: 5.0 5.3 5.3 5.4 5.9 6.2 6.6 6.7 Hypnotized: 5.8 5.9 6.2 6.6 6.7 6.1 7.3 7.4arrow_forward
- The class will include a data exercise where students will be introduced to publicly available data sources. Students will gain experience in manipulating data from the web and applying it to understanding the economic and demographic conditions of regions in the U.S. Regions and topics of focus will be determined (by the student with instructor approval) prior to April. What data exercise can I do to fulfill this requirement? Please explain.arrow_forwardConsider the ceocomp dataset of compensation information for the CEO’s of 100 U.S. companies. We wish to fit aregression model to assess the relationship between CEO compensation in thousands of dollars (includes salary andbonus, but not stock gains) and the following variates:AGE: The CEOs age, in yearsEDUCATN: The CEO’s education level (1 = no college degree; 2 = college/undergrad. degree; 3 = grad. degree)BACKGRD: Background type(1= banking/financial; 2 = sales/marketing; 3 = technical; 4 = legal; 5 = other)TENURE: Number of years employed by the firmEXPER: Number of years as the firm CEOSALES: Sales revenues, in millions of dollarsVAL: Market value of the CEO's stock, in natural logarithm unitsPCNTOWN: Percentage of firm's market value owned by the CEOPROF: Profits of the firm, before taxes, in millions of dollars1) Create a scatterplot matrix for this dataset. Briefly comment on the observed relationships between compensationand the other variates.Note that companies with negative…arrow_forward6 (Model Selection, Estimation and Prediction of GARCH) Consider the daily returns rt of General Electric Company stock (ticker: "GE") from "2021-01-01" to "2024-03-31", comprising a total of 813 daily returns. Using the "fGarch" package of R, outputs of fitting three GARCH models to the returns are given at the end of this question. Model 1 ARCH (1) with standard normal innovations; Model 2 Model 3 GARCH (1, 1) with Student-t innovations; GARCH (2, 2) with Student-t innovations; Based on the outputs, answer the following questions. (a) What can be inferred from the Standardized Residual Tests conducted on Model 1? (b) Which model do you recommend for prediction between Model 2 and Model 3? Why? (c) Write down the fitted model for the model that you recommended in Part (b). (d) Using the model recommended in Part (b), predict the conditional volatility in the next trading day, specifically trading day 814.arrow_forward
- 4 (MLE of ARCH) Suppose rt follows ARCH(2) with E(rt) = 0, rt = ut, ut = στει, σε where {+} is a sequence of independent and identically distributed (iid) standard normal random variables. With observations r₁,...,, write down the log-likelihood function for the model esti- mation.arrow_forward5 (Moments of GARCH) For the GARCH(2,2) model rt = 0.2+0.25u1+0.05u-2 +0.30% / -1 +0.20% -2, find cov(rt). 0.0035 ut, ut = στει,στ =arrow_forwardDefinition of null hypothesis from the textbook Definition of alternative hypothesis from the textbook Imagine this: you suspect your beloved Chicken McNugget is shrinking. Inflation is hitting everything else, so why not the humble nugget too, right? But your sibling thinks you’re just being dramatic—maybe you’re just extra hungry today. Determined to prove them wrong, you take matters (and nuggets) into your own hands. You march into McDonald’s, get two 20-piece boxes, and head home like a scientist on a mission. Now, before you start weighing each nugget like they’re precious gold nuggets, let’s talk hypotheses. The average weight of nuggets as mentioned on the box is 16 g each. Develop your null and alternative hypotheses separately. Next, you weigh each nugget with the precision of a jeweler and find they average out to 15.5 grams. You also conduct a statistical analysis, and the p-value turns out to be 0.01. Based on this information, answer the following questions. (Remember,…arrow_forward
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
