
Concept explainers
(a) A projectile it fired from the origin down an inclined plain: that makes an angle θ with the horizontal. The angle of elevation of the gun and the initial speed of the projectile are α and rv. respectively. Find the position
(b) Show that the angle of elevation α that will maximize the downhill range it the angle halfway between the plane and the vertical.
(c) Suppose the projectile it fired up an inclined plane whose angle of inclination is θ Show that, in order to maximize the (uphill) range, the projectile should be fired in the direction halfway between the plane and the vertical.
(d) In a paper presented in 1686. Edmond Hailey summarized the laws of gravity and projectile motion and applied them to gunnery. One problem he posed involved firing a projectile to hit a target a distance 17 up an inclined plane. Show that the angle at which the projectile should be fired to hit the target but use the least amount of energy is the same as the angle in part (c). (Use the fact that the energy needed to fire the projectile is proportional to the square of the initial speed, so minimizing the energy is equivalent to minimizing the initial speed.)
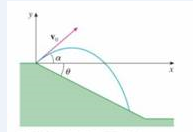
FIGURE FOR PROBLEM 4
Trending nowThis is a popular solution!

Chapter 13 Solutions
Bundle: Multivariable Calculus, 8th + WebAssign Printed Access Card for Stewart's Calculus, 8th Edition, Single-Term
- Find the exact area inside r=2sin(2\theta ) and outside r=\sqrt(3)arrow_forwardA 20 foot ladder rests on level ground; its head (top) is against a vertical wall. The bottom of the ladder begins by being 12 feet from the wall but begins moving away at the rate of 0.1 feet per second. At what rate is the top of the ladder slipping down the wall? You may use a calculator.arrow_forwardExplain the focus and reasons for establishment of 12.4.1(root test) and 12.4.2(ratio test)arrow_forward
- Use 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forwarduse Cauchy Mean-Value Theorem to derive Corollary 12.6.2, and then derive 12.6.3arrow_forwardExplain the focus and reasons for establishment of 12.5.4arrow_forward
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning




