
Concept explainers
PROBLEM PLUS
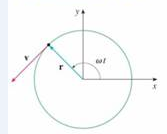
FIGURE FOR PROBLEM 1
1. A particle P moves with constant angular speed ω around a circle whose center is at the origin and whose radius is R. The particle is said to be in uniform circular motion. Assume that the motion is counterclockwise and that the panicle is at the point (R, 0) when t = 0, The position
(a) Find the velocity vector v and show that v · r = 0, Conclude that v is tangent to the circle and points in the direction of the motion
(b) Show that the speed |v| of the particle is the constant ωR. The period T of the particle is the time required for one complete resolution. Conclude that
(c) Find the acceleration vector a. Show that it is proportional to r and that it points toward the origin. An acceleration with this property is called a centripetal acceleration. Show that the magnitude of the acceleration vector is |a| = Rω2.
(d) Suppose that the particle has mass m. Show that the magnitude of the force F that is required to produce this, motion, called a centripetal force. is
Want to see the full answer?
Check out a sample textbook solution
Chapter 13 Solutions
Bundle: Multivariable Calculus, 8th + WebAssign Printed Access Card for Stewart's Calculus, 8th Edition, Single-Term
- (10) (16 points) Let R>0. Consider the truncated sphere S given as x² + y² + (z = √15R)² = R², z ≥0. where F(x, y, z) = −yi + xj . (a) (8 points) Consider the vector field V (x, y, z) = (▼ × F)(x, y, z) Think of S as a hot-air balloon where the vector field V is the velocity vector field measuring the hot gasses escaping through the porous surface S. The flux of V across S gives the volume flow rate of the gasses through S. Calculate this flux. Hint: Parametrize the boundary OS. Then use Stokes' Theorem. (b) (8 points) Calculate the surface area of the balloon. To calculate the surface area, do the following: Translate the balloon surface S by the vector (-15)k. The translated surface, call it S+ is part of the sphere x² + y²+z² = R². Why do S and S+ have the same area? ⚫ Calculate the area of S+. What is the natural spherical parametrization of S+?arrow_forward(1) (8 points) Let c(t) = (et, et sint, et cost). Reparametrize c as a unit speed curve starting from the point (1,0,1).arrow_forward(9) (16 points) Let F(x, y, z) = (x² + y − 4)i + 3xyj + (2x2 +z²)k = - = (x²+y4,3xy, 2x2 + 2²). (a) (4 points) Calculate the divergence and curl of F. (b) (6 points) Find the flux of V x F across the surface S given by x² + y²+2² = 16, z ≥ 0. (c) (6 points) Find the flux of F across the boundary of the unit cube E = [0,1] × [0,1] x [0,1].arrow_forward
- (8) (12 points) (a) (8 points) Let C be the circle x² + y² = 4. Let F(x, y) = (2y + e²)i + (x + sin(y²))j. Evaluate the line integral JF. F.ds. Hint: First calculate V x F. (b) (4 points) Let S be the surface r² + y² + z² = 4, z ≤0. Calculate the flux integral √(V × F) F).dS. Justify your answer.arrow_forwardDetermine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. a = 13, b = 15, C = 68° Law of Sines Law of Cosines Then solve the triangle. (Round your answers to four decimal places.) C = 15.7449 A = 49.9288 B = 62.0712 × Need Help? Read It Watch Itarrow_forward(4) (10 points) Evaluate √(x² + y² + z²)¹⁄² exp[}(x² + y² + z²)²] dV where D is the region defined by 1< x² + y²+ z² ≤4 and √√3(x² + y²) ≤ z. Note: exp(x² + y²+ 2²)²] means el (x²+ y²+=²)²]¸arrow_forward
- (2) (12 points) Let f(x,y) = x²e¯. (a) (4 points) Calculate Vf. (b) (4 points) Given x directional derivative 0, find the line of vectors u = D₁f(x, y) = 0. (u1, 2) such that the - (c) (4 points) Let u= (1+3√3). Show that Duƒ(1, 0) = ¦|▼ƒ(1,0)| . What is the angle between Vf(1,0) and the vector u? Explain.arrow_forwardFind the missing values by solving the parallelogram shown in the figure. (The lengths of the diagonals are given by c and d. Round your answers to two decimal places.) a b 29 39 66.50 C 17.40 d 0 54.0 126° a Ꮎ b darrow_forward(5) (10 points) Let D be the parallelogram in the xy-plane with vertices (0, 0), (1, 1), (1, 1), (0, -2). Let f(x,y) = xy/2. Use the linear change of variables T(u, v)=(u,u2v) = (x, y) 1 to calculate the integral f(x,y) dA= 0 ↓ The domain of T is a rectangle R. What is R? |ǝ(x, y) du dv. |ð(u, v)|arrow_forward
- 2 Anot ined sove in peaper PV+96252 Q3// Find the volume of the region between the cylinder z = y2 and the xy- plane that is bounded by the planes x=1, x=2,y=-2,andy=2. vertical rect a Q4// Draw and Evaluate Soxy-2sin (ny2)dydx D Lake tarrow_forwardDetermine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. B 13 cm 97° Law of Sines Law of Cosines A 43° Then solve the triangle. (Round your answers to two decimal places.) b = x C = A = 40.00arrow_forwardFind the missing values by solving the parallelogram shown in the figure. (The lengths of the diagonals are given by c and d. Round your answers to two decimal places.) a 29 b 39 d Ꮎ 126° a Ꮎ b darrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning



