
Concept explainers
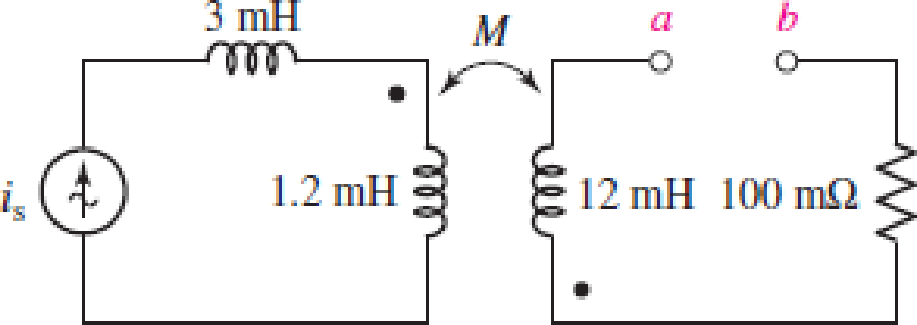
Consider the circuit represented in Fig. 13.53. The coupling coefficient k = 0.75. If is = 5 cos 200t mA, calculate the total energy stored at t = 0 and t = 5 ms if (a) a-b is open-circuited (as shown); (b) a-b is short-circuited.
FIGURE 13.53
(a)
Find the total energy stored in the system at
Answer to Problem 27E
The total energy stored in the system at
Explanation of Solution
Given data:
Refer to Figure 13.53 in the textbook for the given circuit.
The terminals a-b in the given circuit are open circuited.
Formula used:
Write the expression for energy stored in the magnetic field due to self-inductance of the coil at an instant of time as follows:
Here,
Calculation:
As the terminals a-b in the given circuit are open circuited, the current through the secondary winding loop is 0 A. Therefore, the total energy stored in the system is only due to the primary coils of the given circuit.
From the given circuit, find the value of inductance of primary coil when the terminals a-b in the given circuit are open circuited as follows:
Find the current through the primary coil at
Modify the expression in Equation (1) for energy stored in the system due to the coil
Substitute
Find the current through the primary coil at
Modify the expression in Equation (1) for energy stored in the system due to the coil
Substitute
Conclusion:
Thus, the total energy stored in the system at
(b)
Find the total energy stored in the system at
Answer to Problem 27E
The total energy stored in the system at
Explanation of Solution
Given data:
The terminals a-b in the given circuit are short-circuited.
Formula used:
Write the expression for energy stored in the magnetic field due to mutual inductance of the coils at an instant of time as follows:
Here,
Write the expression for mutual inductance in terms of self-inductance of primary and secondary coils as follows:
Here,
Calculation:
Substitute
From the given circuit, find the current
Substitute
Simplify the expression as follows:
Find the current through the secondary coil at
From Part (a), the energy stored in the system due to the coil
Modify the expression in Equation (1) for energy stored in the system due to the coil
Substitute
Rearrange the expression in Equation (2) to find the energy stored in the magnetic field due to the mutual inductance of the coils at
Substitute
Write the expression for total energy stored in the system at
Substitute
From Part (a), the energy stored in the system due to the coil
Find the current through the secondary coil at
Modify the expression in Equation (1) for energy stored in the system due to the coil
Substitute
Rearrange the expression in Equation (2) to find the energy stored in the magnetic field due to the mutual inductance of the coils at
Substitute
Modify the expression in Equation (4) for total energy stored in the system at
Substitute
Conclusion:
Thus, the total energy stored in the system at
Want to see more full solutions like this?
Chapter 13 Solutions
Engineering Circuit Analysis
- "I need an expert solution because the previous solution is incorrect." An antenna with a radiation impedance of 75+j10 ohm, with 10 ohm loss resistance, is connected to a generator with open-circuit voltage of 12 v and an internal impedance of 20 ohms via a 2/4-long transmission line with characteristic impedance of 75 ohms. (a) Draw the equivalent circuit (b) Determine the power supplied by the generator. (c) Determine the power radiated by the antenna. (d) Determine the reflection coefficient at the antenna terminals.arrow_forward--3/5- b) g(t) = 3 1441 g(t+mT) = g(t) -31 (i) Complex fourier coefficient Cn. (ii) Complex fourier coefficients - real fourier coefficient (the first 5 non-zero terms) of (iii) sketch the amplitude spectrum g(t) |Cal against n. n= -3 ⇒n=3 (labelling the axis).arrow_forwardQ4) (i) Calculate the fourier transform of : h(t) 2T (is) h(t) 2T -T о T 2T ·(-++T). cos2t ost≤T (iii) hro (4) ((-++T). cos otherwisearrow_forward
- Q2)a) consider the Circuit in figure 2 with initial conditions of Vc (o) = 5V, I₁ (o) = 1A, (i) redraw the circuit in the frequency domain using laplace Wansforms. (ii) using this circuit derive an equation for the Voltage across the inductor in the time domain.. 3.12 ww =V/3F ZH (figure 2) d) Solve the following second order differential equation using laplace transforms. d12 + 5 dx 3x=71 dt - with initial conditions x² (0) = 2, α(0) = 1arrow_forwardb) Another periodic waveform is defined by T c) g(t)= T with g(t+mT) = g(t) and m is an integer. (i) Sketch g(t) over two full cycles in the time domain, labelling the axes. (ii) Derive the formulae for the complex Fourier coefficients c₁ for g(t). For a periodic waveform h(t), if its complex Fourier coefficients are T T when n is odd T 2n²² T 4nn when n is even and not zero 4nn please derive the first five non-zero terms of the real Fourier series for h(t).arrow_forwardQ3)α) f(t) = (-+- 1 Isto f(t+mT) = f(t). L+- I Ost ST integer (i) sketch f(t) 2 full cycles time domain. (labelling the axis). (ii) Derive the formula for the real fourier Coefficients (i) Real Fourier series f(t), first 5 non-terms. an bn for f(t).arrow_forward
- Q3. a) A periodic waveform is defined by T 3 0≤t< f(t) = SIarrow_forwardQ2. a) Sketch the following waveform f(t)=Vo -1/2≤t≤1/2 =0 otherwise and show that its Fourier transform is 2V ωτ ωτ F(s)-sinotsinc) 2 Use this result to sketch a fully labelled graph of the amplitude spectrum of a single square voltage pulse, of amplitude 24V and pulse width 1.4μs, using units of Hz for the frequency axis. (Note: graph paper is not required - a clear, fully-labelled sketch is adequate).arrow_forwardc) Another periodic waveform is defined by 4t g(t)= 0≤tarrow_forwardQ1. a) A periodic waveform is defined by f(t)= 3 0≤tarrow_forwardI have 50mV in the function generator with 10kHz. Does the connection and reading seem about right? I need to read output voltage.arrow_forwardThe solution sent previously is incorrect; I need the correct solution. An antenna with a radiation impedance of 75+j10 ohm, with 10 ohm loss resistance, is connected to a generator with open-circuit voltage of 12 v and an internal impedance of 20 ohms via a 2/4-long transmission line with characteristic impedance of 75 ohms. (a) Draw the equivalent circuit (c) Determine the power radiated by the antenna.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,TRANSFORMERS - What They Are, How They Work, How Electricians Size Them; Author: Electrician U;https://www.youtube.com/watch?v=tXPy4OE7ApE;License: Standard Youtube License
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,TRANSFORMERS - What They Are, How They Work, How Electricians Size Them; Author: Electrician U;https://www.youtube.com/watch?v=tXPy4OE7ApE;License: Standard Youtube License