
Concept explainers
The wood column has a thickness of 4 in. and a width of 6 in. Using the NFPA equations of Sec.13.6 and Eq.13-30, determine the maximum allowable eccentric load P that can be applied. Assume that the column is pinned at both its top and bottom.
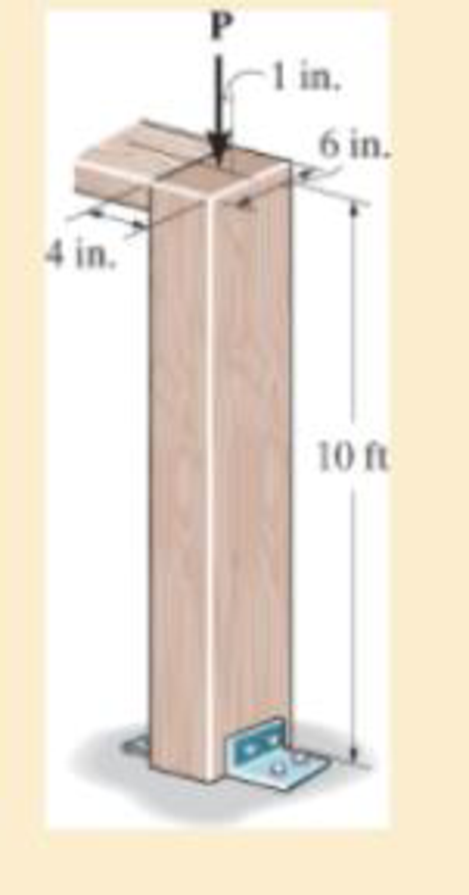
R13−1
Answer to Problem 1RP
The maximum allowable eccentric load on the column is
Explanation of Solution
Given information:
The load applied on the wooden column is
The column is pinned at both the ends.
The width of cross-sectional area of the column is
The depth of cross-sectional area of the column is
The length of the column is
Show the expression ofNFPA Equation of Sec 13.6 as follows:
Here,
Show the expression for Equation 13-30 as follows:
Here,
Calculation:
Calculate the cross-sectional area
Substitute
Calculate the moment of inertia using the relation:
Substitute
The ends of the column are pinned. Thus, the value of
Calculate the value of
Substitute
The value of
Show the expression of NFPA Equation of Sec 13.6 as follows:
Here,
Substitute 30 for
Show the expression for Equation 13-30 as follows:
Here,
The eccentricity
Calculate the value of c using the relation:
Substitute
Substitute
Thus, the maximum allowable eccentric load on the column is
Want to see more full solutions like this?
Chapter 13 Solutions
Mechanics of Materials
Additional Engineering Textbook Solutions
Modern Database Management
Fluid Mechanics: Fundamentals and Applications
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Java: An Introduction to Problem Solving and Programming (8th Edition)
Automotive Technology: Principles, Diagnosis, And Service (6th Edition) (halderman Automotive Series)
Vector Mechanics for Engineers: Statics and Dynamics
- What is the difference between saturated liquid and compressed liquid? What is the difference between the critical point and the triple pointarrow_forwardWhat is quality? Does it have any meaning in the superheated vapour region? What is the difference between saturated vapor and superheated vapour? What is the difference between saturated liquid and compressed liquid? What is the difference between the critical point and the triple point?arrow_forwardHomework#5arrow_forward
- Describe the principle operation of PEMFC, and role of membrane electrode assembly (MEA).arrow_forwardHomework#5arrow_forwardUsing graphical methods, draw the pressure angle at the position shown in (a) and (b). e |------- R = Cam Base Radius e = Follower Offset ẞ₁ = Section Duration 1 B₁ = Section Duration 2 ẞ₂ = Section Duration 3 В2 B₁ Follower Position ww R ẞ3 (a) Reference Radial (b)arrow_forward
- The figure below illustrates a graph that has a variable load torque and constant drive torque. Each cycle lasts three revolutions (6л radians). Torque (N-m) 600 550 400 1 200 TD= 225 N-m 2 + -T₁ 3 4 1 + 0 In addition, the rotation speed is @o steady-state conditions, determine 1. the average power required, 2πT 4π 5πT 6п Ꮎ = 180° rpm = 18.85 rad/sec, Imachine 125 kg-m². Assuming 2. the maximum and minimum rotational speeds throughout a cycle, 3. the mass of a 0.6-meter-diameter solid disc flywheel to produce Cs = 0.025.arrow_forwardAn elastic cord is stretched between 2 points A and B located 2y = 0.8 m apart in the horizontal plane. When stretched directly between A and B, the tension is P₂ = 40 N. The cord is then stretched as shown until its midpoint C has moved through x = 0.3 m to C', and a force of F = 240 N is required to hold the cord at C'. A pellet (m = 0.1 kg) is placed at C' and the cord is released. Find the speed of the pellet as it passes through C.arrow_forwardA 6305 ball bearing is subjected to a steady 5000-N radial load and a 2000-N thrust load and uses a very clean lubricant throughout its life. If the inner race angular velocity is 500rpm find (a) The equivalent radial load (b) The L10 life (c) The L50 lifearrow_forward
- Slove this the question plearrow_forwardDetermine the Mean Effective Pressure (MEP) in [bar] for a 4-cylinder, 2-Stroke engine with a bore of 85.7 mm, and a stroke of 65.8 mm, that produces 85 hP at 5000 rpm. (Hint: Be careful with units). Note: 1 hP = 0.7457 kW; 100 kPa = 1 bararrow_forwardIbraheem Super Q3: A boiler as shown in the figure below is producing 2 kg/s saturated steam at 240C. The water enters the boiler at 24C. The boiler efficiency is 80%. Patm=1.05 bar .Determine: (10 Marks) 1- The inlet pressure of the turbine. 2- If a gauge pressure connected to the outlet pipe, what is the reading of this gauge? 3- Calculate the required diesel in [kg/s]. Assume the calorific value of the diesel is 45000 kJ/kgf 4- Calculate the equivalent evaporation of the boiler 5- Keeping the same inlet conditions and fuel consumption, determine the turbine efficiency if the produced steam was saturated at 300C. Steam Cut Hot Gasses Out Ts=240C Boiler FURNACE A Water In C 24 Examiner Head of Department Ahmad. A. M. Alsak laniarrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
