
EBK CALCULUS & ITS APPLICATIONS
14th Edition
ISBN: 8220103679527
Author: Asmar
Publisher: YUZU
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 1.3, Problem 1CYU
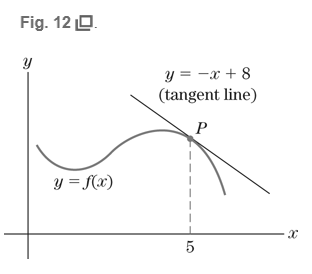
Consider the curve
Find
Find
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Question 1:
If a barometer were built using oil (p = 0.92 g/cm³) instead of mercury (p =
13.6 g/cm³), would the column of oil be higher than, lower than, or the same as the
column of mercury at 1.00 atm? If the level is different, by what factor? Explain. (5 pts)
Solution:
A barometer works based on the principle that the pressure exerted by the liquid column
balances atmospheric pressure. The pressure is given by:
P = pgh
Since the atmospheric pressure remains constant (P = 1.00 atm), the height of the
liquid column is inversely proportional to its density:
Step 1: Given Data
PHg
hol=hgx
Poil
• Density of mercury: PHg = 13.6 g/cm³
Density of oil: Poil = 0.92 g/cm³
• Standard height of mercury at 1.00 atm: hμg
Step 2: Compute Height of Oil
= 760 mm = 0.760 m
13.6
hoil
= 0.760 x
0.92
hoil
= 0.760 × 14.78
hoil
= 11.23 m
Step 3: Compare Heights
Since oil is less dense than mercury, the column of oil must be much taller than that of
mercury. The factor by which it is taller is:
Final…
Question 3:
A sealed flask at room temperature contains a mixture of neon (Ne) and nitrogen (N2)
gases.
Ne has a mass of 3.25 g and exerts a pressure of 48.2 torr.
.
N2 contributes a pressure of 142 torr.
• What is the mass of the N2 in the flask?
• Atomic mass of Ne = 20.1797 g/mol
• Atomic mass of N = 14.0067 g/mol
Solution:
We will use the Ideal Gas Law to determine the number of moles of each gas and
calculate the mass of N2.
PV = nRT
where:
• P = total pressure
•
V volume of the flask (same for both gases)
n = number of moles of gas
•
R 0.0821 L atm/mol K
• T = Room temperature (assume 298 K)
Since both gases are in the same flask, their partial pressures correspond to their mole
fractions.
Step 1: Convert Pressures to Atmospheres
48.2
PNe
= 0.0634 atm
760
142
PN2
=
= 0.1868 atm
760
Step 2: Determine Moles of Ne
nNe =
mass
molar mass
3.25
nNe
20.1797
nne 0.1611 mol
Step 3: Use Partial Pressure Ratio to Find n
"I have written solutions in text form, but I need experts to rewrite them in handwriting from A to Z, exactly as I have written, without any changes."
Chapter 1 Solutions
EBK CALCULUS & ITS APPLICATIONS
Ch. 1.1 - Find the slope of the following lines. The line...Ch. 1.1 - Find the slopes of the following lines. The line...Ch. 1.1 - Find the slopes and y-intercepts of the following...Ch. 1.1 - Find the slopes and y-intercepts of the following...Ch. 1.1 - Find the slopes and y-intercepts of the following...Ch. 1.1 - Find the slopes and y-intercepts of the following...Ch. 1.1 - Find the slopes and y-intercepts of the following...Ch. 1.1 - Find the slopes and y-intercepts of the following...Ch. 1.1 - Find an equation of the given line. Slope is 1;...Ch. 1.1 - Find an equation of the given line. Slope is 2;...
Ch. 1.1 - Find an equation of the given line. Slope is 12;...Ch. 1.1 - Prob. 10ECh. 1.1 - Find an equation of the given line. (57,5) and...Ch. 1.1 - Find an equation of the given line. (12,1) and...Ch. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Find an equation of the given line. Horizontal...Ch. 1.1 - Find an equation of the given line. x intercept is...Ch. 1.1 - Find an equation of the given line. x intercept is...Ch. 1.1 - Find an equation of the given line. Slope is 2;x...Ch. 1.1 - Find an equation of the given line. Slope is 2;x...Ch. 1.1 - Find an equation of the given line. Horizontal...Ch. 1.1 - Find an equation of the given line. Parallel to...Ch. 1.1 - Find an equation of the given line. Parallel to...Ch. 1.1 - Find an equation of the given line. Parallel to...Ch. 1.1 - Find an equation of the given line. Parallel to...Ch. 1.1 - Find an equation of the given line. Perpendicular...Ch. 1.1 - Prob. 26ECh. 1.1 - In Exercises 2730, we specify a line by giving the...Ch. 1.1 - Prob. 28ECh. 1.1 - In Exercises 2730, we specify a line by giving the...Ch. 1.1 - Prob. 30ECh. 1.1 - Each of lines (A),(B),(C),and(D) in the figure is...Ch. 1.1 - The line through the points (1,2)and(3,b) is...Ch. 1.1 - In Exercises 3336, refer to a line of slope m. If...Ch. 1.1 - In Exercises 3336, refer to a line of slope m. If...Ch. 1.1 - In Exercises 3336, refer to a line of slope m. If...Ch. 1.1 - Prob. 36ECh. 1.1 - In Exercises 37and38, we specify a line by giving...Ch. 1.1 - In Exercises 37and38, we specify a line by giving...Ch. 1.1 - In Exercises 37and38, we specify a line by giving...Ch. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Find the equation and sketch the graph of the...Ch. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Marginal Cost Let C(x)=12x+1100 denote the total...Ch. 1.1 - Refer to Exercise 47. Use the formula for C(x) to...Ch. 1.1 - Price of Gasoline The price of 1 gallon of...Ch. 1.1 - Impact of Mad Cow Disease on Canadian Beef Exports...Ch. 1.1 - Cost of Shipping and Handling An online bookstore...Ch. 1.1 - Quit Ratio In industry, the relationship between...Ch. 1.1 - Price Affects Sales When the owner of a gas...Ch. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Interpreting the Slope and y -Intercept A...Ch. 1.1 - Interpreting the Slope and y -Intercept The demand...Ch. 1.1 - Converting Fahrenheit to Celsius Temperatures of...Ch. 1.1 - Prob. 59ECh. 1.1 - Refer to Exercise 59. If the patient's body...Ch. 1.1 - Prob. 61ECh. 1.1 - Diver's Ascent The diver in the previous exercise...Ch. 1.1 - Prob. 63ECh. 1.1 - Breakeven In order for a business to break even,...Ch. 1.1 - If, for some constant m, f(x2)f(x1)x2x1=m for all...Ch. 1.1 - a. Draw the graph of any function f(x) that passes...Ch. 1.1 - Urban World Population Let y denotes the...Ch. 1.1 - Technology Exercises Let y denote the average...Ch. 1.2 - What is the slope of the curve at (3,4)? What is...Ch. 1.2 - What is the equation of the tangent line to the...Ch. 1.2 - Estimate the slope of each of the following curves...Ch. 1.2 - Estimate the slope of each of the following curves...Ch. 1.2 - Estimate the slope of each of the following curves...Ch. 1.2 - Estimate the slope of each of the following curves...Ch. 1.2 - Estimate the slope of each of the following curves...Ch. 1.2 - Estimate the slope of each of the following curves...Ch. 1.2 - Estimate the slope of each of the following curves...Ch. 1.2 - Estimate the slope of each of the following curves...Ch. 1.2 - Exercise 9-12 refer to the points in Fig.12....Ch. 1.2 - Exercises 9-12 refer to the points in Fig.12....Ch. 1.2 - Exercises 9-12 refer to the points in Fig.12....Ch. 1.2 - Exercises 9-12 refer to the points in Fig.12....Ch. 1.2 - In Exercises 13-20, find the slope of the tangent...Ch. 1.2 - In Exercises 13-20, find the slope of the tangent...Ch. 1.2 - In Exercises 13-20, find the slope of the tangent...Ch. 1.2 - In Exercises 13-20, find the slope of the tangent...Ch. 1.2 - In Exercises 13-20, find the slope of the tangent...Ch. 1.2 - In Exercises 13-20, find the slope of the tangent...Ch. 1.2 - In Exercises 13-20, find the slope of the tangent...Ch. 1.2 - In Exercises 13-20, find the slope of the tangent...Ch. 1.2 - Find the point on the graph y=x2 where the curve...Ch. 1.2 - Find the point on the graph y=x2 where the curve...Ch. 1.2 - Find the point on the graph of y=x2 where the...Ch. 1.2 - Find the point on the graph of y=x2 where the...Ch. 1.2 - Price of Crude Oil Figure shows the price of 1...Ch. 1.2 - Refer to the Fig.13. Do you agree with the...Ch. 1.2 - Refer to Fig.14, which shows an enlarged version...Ch. 1.2 - Refer to Fig.14. Estimate the price of one barrel...Ch. 1.2 - In the next section we shall see that the tangent...Ch. 1.2 - In the next section we shall see that the tangent...Ch. 1.2 - In the next section we shall see that the tangent...Ch. 1.2 - In the next section we shall see that the tangent...Ch. 1.2 - In Exercise 33 and 34, you are shown the tangent...Ch. 1.2 - In Exercise 33 and 34, you are shown the tangent...Ch. 1.2 - Find the point(s) on the graph in fig 15 where the...Ch. 1.2 - Prob. 36ECh. 1.2 - Let l be the line through the points P and Q in...Ch. 1.2 - In Fg.17, h represents a positive number, and 3+h...Ch. 1.2 - Technology Exercises In Exercises 39-42 you are...Ch. 1.2 - Prob. 40ECh. 1.2 - Technology Exercises In Exercises 39-42 you are...Ch. 1.2 - Technology Exercises In Exercises 39-42 you are...Ch. 1.3 - Consider the curve y=f(x) in Fig. 12. Find f(5)....Ch. 1.3 - Let f(x)=1/x4. a. Find its derivative. b. Find...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - Use formulas (1) and (2) and the power rule to...Ch. 1.3 - In Exercises 1724, find the derivative of f(x) at...Ch. 1.3 - In Exercises 1724, find the derivative of f(x) at...Ch. 1.3 - In Exercises 1724, find the derivative of f(x) at...Ch. 1.3 - In Exercises 1724, find the derivative of f(x) at...Ch. 1.3 - In Exercises 1724, find the derivative of f(x) at...Ch. 1.3 - In Exercises 1724, find the derivative of f(x) at...Ch. 1.3 - In Exercises 1724, find the derivative of f(x) at...Ch. 1.3 - In Exercises 1724, find the derivative of f(x) at...Ch. 1.3 - Find the slope of the curve y=x4 at x=2.Ch. 1.3 - Find the slope of the curve y=x5 at x=13.Ch. 1.3 - If f(x)=x3, compute f(5) and f(5).Ch. 1.3 - If f(x)=2x+6, compute f(0) and f(0).Ch. 1.3 - If f(x)=x1/3, compute f(8) and f(8).Ch. 1.3 - If f(x)=1/x2, compute f(1) and f(1).Ch. 1.3 - If f(x)=1/x5, compute f(2) and f(2).Ch. 1.3 - If f(x)=x3/2, compute f(16) and f(16).Ch. 1.3 - In Exercises 33-40, find an equation of the...Ch. 1.3 - In Exercises 33-40, find an equation of the...Ch. 1.3 - In Exercises 33-40, find an equation of the...Ch. 1.3 - In Exercises 33-40, find an equation of the...Ch. 1.3 - In Exercises 33-40, find an equation of the...Ch. 1.3 - In Exercises 33-40, find an equation of the...Ch. 1.3 - In Exercises 33-40, find an equation of the...Ch. 1.3 - In Exercises 33-40, find an equation of the...Ch. 1.3 - The point-slope form of the equation of the...Ch. 1.3 - The tangent line to the graph of y=1x at the point...Ch. 1.3 - The line y=2x+b is tangent to the graph y=x at the...Ch. 1.3 - The line y=ax+b is tangent to the graph of y=x3 at...Ch. 1.3 - a. Find the point on the curve y=x where the...Ch. 1.3 - There are two points on the graph of y=x3 where...Ch. 1.3 - Is there any point on the graph of y=x3 where the...Ch. 1.3 - The graph of y=f(x) goes through the point (2, 3)...Ch. 1.3 - In Exercises 4956, find the indicated derivatives....Ch. 1.3 - In Exercises 4956, find the indicated derivative....Ch. 1.3 - In Exercises 4956, find the indicated derivative....Ch. 1.3 - In Exercises 4956, find the indicated derivative....Ch. 1.3 - In Exercises 4956, find the indicated derivative....Ch. 1.3 - In Exercises 4956, find the indicated derivative....Ch. 1.3 - In Exercises 4956, find the indicated derivative....Ch. 1.3 - In Exercises 4956, find the indicated derivative....Ch. 1.3 - Consider the curve y=f(x) in Fig.13. Find f(6) and...Ch. 1.3 - Consider the curve y=f(x) in Fig.14. Find f(1) and...Ch. 1.3 - In Fig.15, the straight line y=14x+b is tangent to...Ch. 1.3 - In Fig.16, the straight line is tangent to the...Ch. 1.3 - Consider the curve y=f(x) in Fig.17. Find a and...Ch. 1.3 - Consider the curve y=f(x) in Fig.18. Estimate f(1)...Ch. 1.3 - In Fig 19, find the equation of the tangent line...Ch. 1.3 - In Fig 20, find the equation of tangent line to...Ch. 1.3 - In Exercises 65-70, compute the difference...Ch. 1.3 - In Exercises 65-70, compute the difference...Ch. 1.3 - In Exercises 65-70, compute the difference...Ch. 1.3 - In Exercises 65-70, compute the difference...Ch. 1.3 - In Exercises 65-70, compute the difference...Ch. 1.3 - In Exercises 65-70, compute the difference...Ch. 1.3 - In Exercises 71-76, apply the three step method to...Ch. 1.3 - In Exercises 71-76, apply the three step method to...Ch. 1.3 - In Exercises 71-76, apply the threestep method to...Ch. 1.3 - In Exercises 71-76, apply the three step method to...Ch. 1.3 - In Exercises 71-76, apply the three step method to...Ch. 1.3 - In Exercises 71-76, apply the three step method to...Ch. 1.3 - Draw two graphs of your choice that represent a...Ch. 1.3 - Use the approach of Exercise 77 to show that...Ch. 1.3 - Prob. 79ECh. 1.3 - Prob. 80ECh. 1.3 - Technology Exercises In Exercises 79-84, use a...Ch. 1.3 - Technology Exercises In Exercises 79-84, use a...Ch. 1.3 - Technology Exercises In Exercises 79-84, use a...Ch. 1.3 - Technology Exercises In Exercises 79-84, use a...Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - For each of the following functions g(x), dtermine...Ch. 1.4 - For each of the following functions g(x), dtermine...Ch. 1.4 - For each of the following functions g(x), dtermine...Ch. 1.4 - For each of the following functions g(x), dtermine...Ch. 1.4 - For each of the following functions g(x), dtermine...Ch. 1.4 - For each of the following functions g(x), dtermine...Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Prob. 13ECh. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Determine which of the following limits exist....Ch. 1.4 - Prob. 26ECh. 1.4 - Compute the limits that exist, given that...Ch. 1.4 - Use the limit definition of the derivative to show...Ch. 1.4 - Use limits to compute the following derivatives....Ch. 1.4 - Use limits to compute the following derivatives....Ch. 1.4 - Use limits to compute the following derivatives....Ch. 1.4 - Use limits to compute the following derivatives....Ch. 1.4 - In Exercise 3336, apply the three- step method to...Ch. 1.4 - In Exercises 33-36, apply the three step method to...Ch. 1.4 - In Exercises 33-36, apply the three step method to...Ch. 1.4 - In Exercises 33-36, apply the three step method to...Ch. 1.4 - In Exercises 37-48, use limits to compute f(x)....Ch. 1.4 - In Exercises 37-48, use limits to compute f(x)....Ch. 1.4 - In Exercises 37-48, use limits to compute f(x)....Ch. 1.4 - In Exercises 37-48, use limits to compute f(x)....Ch. 1.4 - In Exercises 37-48, use limits to compute f(x)....Ch. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - In Exercises 37-48, use limits to compute f(x)....Ch. 1.4 - Prob. 49ECh. 1.4 - Each limit in Exercises 49-54 is a definition of...Ch. 1.4 - Each limit in Exercises 49-54 is a definition of...Ch. 1.4 - Each limit in Exercises 49-54 is a definition of...Ch. 1.4 - Each limit in Exercises 49-54 is a definition of...Ch. 1.4 - Each limit in Exercises 49-54 is a definition of...Ch. 1.4 - Compute the following limits. limx1x2Ch. 1.4 - Compute the following limits. limx1x2Ch. 1.4 - Compute the following limits. limx5x+33x2Ch. 1.4 - Compute the following limits. limx1x8Ch. 1.4 - Compute the following limits. limx10x+100x230Ch. 1.4 - Compute the following limits. limxx2+xx21Ch. 1.4 - In Exercises 61-66, refer to Fig. to find the...Ch. 1.4 - In Exercises 61-66, refer to Fig. to find the...Ch. 1.4 - In Exercises 61-66, refer to Fig. to find the...Ch. 1.4 - In Exercises 61-66, refer to Fig. to find the...Ch. 1.4 - In Exercises 61-66, refer to Fig. to find the...Ch. 1.4 - In Exercises 61-66, refer to Fig. to find the...Ch. 1.4 - Technology Exercises Examine the graph of the...Ch. 1.4 - Technology Exercises Examine the graph of the...Ch. 1.4 - Technology Exercises Examine the graph of the...Ch. 1.4 - Technology Exercises Examine the graph of the...Ch. 1.5 - Let f(x)={ x2x6x3forx34forx=3. Is f(x) continuous...Ch. 1.5 - Let f(x)={ x2x6x3forx34forx=3. Is f(x)...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Is the function whose graph is drawn in Fig.,...Ch. 1.5 - Prob. 12ECh. 1.5 - Determine whether each of the following functions...Ch. 1.5 - Prob. 14ECh. 1.5 - Determine whether each of the following functions...Ch. 1.5 - Prob. 16ECh. 1.5 - Determine whether each of the following functions...Ch. 1.5 - Determine whether each of the following functions...Ch. 1.5 - Determine whether each of the following functions...Ch. 1.5 - Determine whether each of the following functions...Ch. 1.5 - The functions in Exercise 21 -26 are defined for...Ch. 1.5 - Prob. 22ECh. 1.5 - The functions in Exercise 21 -26 are defined for...Ch. 1.5 - The functions in Exercise 21 -26 are defined for...Ch. 1.5 - The functions in Exercise 21 -26 are defined for...Ch. 1.5 - The functions in Exercise 21 -26 are defined for...Ch. 1.5 - Computing Income Tax The tax that you pay to the...Ch. 1.5 - Prob. 28ECh. 1.5 - Revenue from Sales The owner of a photocopy store...Ch. 1.5 - Do Exercise 29 if cost 10 cents per copy for the...Ch. 1.5 - Department Store Sales The graphs in Fig. 8 shows...Ch. 1.5 - Refer to Exercise 31. From midnight to noon, which...Ch. 1.5 - Prob. 33ECh. 1.5 - In Exercise 33 and 34, determine the value of a...Ch. 1.6 - Find the derivative ddx(x).Ch. 1.6 - Differentiate the function y=x+(x5+1)103.Ch. 1.6 - Differentiate. y=6x3Ch. 1.6 - Differentiate. y=3x4Ch. 1.6 - Differentiate. y=3x3Ch. 1.6 - Differentiate. y=13x3Ch. 1.6 - Differentiate. y=x22xCh. 1.6 - Differentiate. f(x)=12+173Ch. 1.6 - Differentiate. f(x)=x4+x3+xCh. 1.6 - Differentiate. y=4x32x2+x+1Ch. 1.6 - Differentiate. y=(2x+4)3Ch. 1.6 - Differentiate. y=(x21)3Ch. 1.6 - Differentiate. y=(x3+x2+1)7Ch. 1.6 - Differentiate. y=(x2+x)2Ch. 1.6 - Differentiate. y=4x2Ch. 1.6 - Differentiate. y=4(x26)3Ch. 1.6 - Differentiate. y=32x2+13Ch. 1.6 - Differentiate. y=2x+1Ch. 1.6 - Differentiate. y=2x+(x+2)2Ch. 1.6 - Differentiate. y=(x1)3+(x+2)4Ch. 1.6 - Differentiate. y=15x5Ch. 1.6 - Differentiate. y=(x2+1)2+3(x21)2Ch. 1.6 - Differentiate. y=1x3+1Ch. 1.6 - Differentiate. y=2x+1Ch. 1.6 - Prob. 23ECh. 1.6 - Differentiate. y=2x2+14Ch. 1.6 - Differentiate. f(x)=53x3+xCh. 1.6 - Differentiate. y=1x3+x+1Ch. 1.6 - Differentiate. y=3x+3Ch. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Differentiate. y=12x+5Ch. 1.6 - Differentiate. y=215xCh. 1.6 - Differentiate. y=71+xCh. 1.6 - Differentiate. y=451+x+xCh. 1.6 - Differentiate. y=(1+x+x2)11Ch. 1.6 - Prob. 35ECh. 1.6 - Differentiate. y=2xCh. 1.6 - Differentiate. f(x)=(x2+1)3/2Ch. 1.6 - Differentiate. y=(x1x)1Ch. 1.6 - In Exercises 39 and 40, find the slope of the...Ch. 1.6 - In Exercises 39 and 40, find the slope of the...Ch. 1.6 - Find the slope of the tangent line to the curve...Ch. 1.6 - Write the equation of the tangent line to the...Ch. 1.6 - Find the slope of the tangent line to the curve...Ch. 1.6 - Find the equation of the tangent line to the curve...Ch. 1.6 - Differentiate the function f(x)=(3x2+x2)2 in two...Ch. 1.6 - Using the sum rule and the constant-multiple rule,...Ch. 1.6 - Figure 2 contains the curves y=f(x) and y=g(x) and...Ch. 1.6 - Figure 3 contains the curves...Ch. 1.6 - If f(5)=2,f(5)=3,g(5)=4,andg(5)=1, find...Ch. 1.6 - If g(3)=2andg(3)=4, find f(3)andf(3), where...Ch. 1.6 - It g(1)=4andg(1)=3, find f(1)andf(1), where...Ch. 1.6 - h(x)=[ f(x) ]2+g(x), determine h(1)andh(1), given...Ch. 1.6 - The tangent line to the curve y=13x34x2+18x+22 is...Ch. 1.6 - The tangent line to the curve y=x36x234x9 has...Ch. 1.6 - The straight line in the figure is tangent to the...Ch. 1.6 - The straight line in the figure is tangent to the...Ch. 1.7 - Let f(t)=t+1(1/t). Find f(2).Ch. 1.7 - Differentiate g(r)=2rh.Ch. 1.7 - Find the first derivatives. f(t)(t2+1)5Ch. 1.7 - Find the first derivatives. f(P)=P3+3P27P+2Ch. 1.7 - Find the first derivatives. v(t)=4t2+11t+1Ch. 1.7 - Find the first derivatives. g(y)=y22y+4Ch. 1.7 - Find the first derivatives. y=T54T4+3T2T1Ch. 1.7 - Find the first derivatives. x=16t2+45t+10Ch. 1.7 - Find the first derivatives. Find ddP(3P212P+1)Ch. 1.7 - Find the first derivatives. Find ddss2+1Ch. 1.7 - Find the first derivatives. Find ddP(T2+3P)3Ch. 1.7 - Find the first derivatives. Find ddP(T2+3P)3Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - In Exercises 11-20, find the first and second...Ch. 1.7 - Compute the following. ddx(2x+7)2|x=1Ch. 1.7 - Prob. 22ECh. 1.7 - Compute the following. ddz(z2+2z+1)7|z=1Ch. 1.7 - Compute the following. d2dx2(3x4+4x2)|x=2Ch. 1.7 - Compute the following. d2dx2(3x3x2+7x1)|x=2Ch. 1.7 - Compute the following. ddx(dydx)|x=1, Where...Ch. 1.7 - Compute the following. f(1) and f(1), when...Ch. 1.7 - Compute the following. g(0) and g(0), when...Ch. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Daily Volume of Business A supermarket finds that...Ch. 1.7 - If s=PT, find dsdP, dsdT.Ch. 1.7 - If s=P2T, find d2sdP2 d2sdT2.Ch. 1.7 - If s=Tx2+3xP+T2, find: dsdx dsdP dsdTCh. 1.7 - Prob. 36ECh. 1.7 - Manufacturing Cost Let C(x) be the cost (in...Ch. 1.7 - Estimate the cost of manufacturing 51 bicycles per...Ch. 1.7 - A Revenue Function The revenue from producing (and...Ch. 1.7 - Profit and Marginal Profit Let P(x) be the profit...Ch. 1.7 - Revenue and Marginal Revenue Let R(x) denote the...Ch. 1.7 - Refer to Exercise 41. Is it profitable to produce...Ch. 1.7 - Sales at a Department Store Let S(x) represent the...Ch. 1.7 - Prob. 44ECh. 1.7 - Prob. 45ECh. 1.7 - Correcting a Prediction The financial analysts at...Ch. 1.7 - Prob. 47ECh. 1.7 - Prob. 48ECh. 1.7 - Prob. 49ECh. 1.7 - Prob. 50ECh. 1.7 - Technology Exercises For the given function,...Ch. 1.7 - Prob. 52ECh. 1.8 - Let f(t) be the temperature (In degrees Celsius)...Ch. 1.8 - Let f(t) be the temperature (in degrees Celsius)...Ch. 1.8 - Let f(t) be the temperature (in degrees Celsius)...Ch. 1.8 - Prob. 4CYUCh. 1.8 - Prob. 5CYUCh. 1.8 - Prob. 6CYUCh. 1.8 - If f(x)=x2+3x, calculate the average rate of...Ch. 1.8 - If f(x)=3x2+2, calculate the average rate of...Ch. 1.8 - Average and Instantaneous Rates of Change Suppose...Ch. 1.8 - Average and Instantaneous Rates of Change Suppose...Ch. 1.8 - Average and Instantaneous Rates of Change Suppose...Ch. 1.8 - Average and Instantaneous Rates of Change Suppose...Ch. 1.8 - Motion of an Object An object moving in a straight...Ch. 1.8 - Effect of Advertising on Sales After an...Ch. 1.8 - Average Daily Output An analysis of the daily...Ch. 1.8 - Prob. 10ECh. 1.8 - Maximum Height A toy rocket is fired straight up...Ch. 1.8 - Analysis of a Moving Particle Refer to Fig.6,...Ch. 1.8 - Position of Toy Rocket A toy rocket fired straight...Ch. 1.8 - Height of a Helicopter A helicopter is rising...Ch. 1.8 - Height of a Ball Let s(t) be the height (in feet)...Ch. 1.8 - Average Speed Table 2 gives a cars trip odometer...Ch. 1.8 - Velocity and Position A particle is moving in a...Ch. 1.8 - Interpreting Rates of Change on a Graph A car is...Ch. 1.8 - Estimating the Values of a function If f(100)=5000...Ch. 1.8 - Estimating the Values of a function If f(25)=10...Ch. 1.8 - Temperature of a Cup of Coffee Let f(t) be the...Ch. 1.8 - Rate of Elimination of a Drug Suppose that 5 mg of...Ch. 1.8 - Price Affects Sales Let f(p) be the number of cars...Ch. 1.8 - Advertising Affects Salesdollars are spent on...Ch. 1.8 - Rate of Sales Let f(x) be the number (in...Ch. 1.8 - Marginal Cost Let C(x) be the cost (in dollars) of...Ch. 1.8 - Prob. 27ECh. 1.8 - Price of a Companys Stock Let f(x) be the value in...Ch. 1.8 - Marginal Cost Analysis Consider the cost function...Ch. 1.8 - Estimate how much the function f(x)=11+x2 will...Ch. 1.8 - Health Expenditures National health expenditures...Ch. 1.8 - Velocity and Acceleration In an 8-second test run,...Ch. 1.8 - Technology exercises Judgment Time In a psychology...Ch. 1.8 - Technology Exercises Position of a Ball A ball...Ch. 1 - Define the slope of a nonvertical line and give a...Ch. 1 - What is the point-slope form of the equation of a...Ch. 1 - Describe how to find an equation for a line when...Ch. 1 - Prob. 4CCECh. 1 - Prob. 5CCECh. 1 - Prob. 6CCECh. 1 - Prob. 7CCECh. 1 - Prob. 8CCECh. 1 - Prob. 9CCECh. 1 - Prob. 10CCECh. 1 - Prob. 11CCECh. 1 - Prob. 12CCECh. 1 - Prob. 13CCECh. 1 - Prob. 14CCECh. 1 - State the general power rule and give an example.Ch. 1 - Prob. 16CCECh. 1 - Prob. 17CCECh. 1 - Prob. 18CCECh. 1 - Prob. 19CCECh. 1 - Prob. 20CCECh. 1 - Prob. 21CCECh. 1 - Prob. 22CCECh. 1 - Find the equation and sketch the graph of the...Ch. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Find the equation and sketch the graph of the...Ch. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Differentiate. y=x7+x3Ch. 1 - Differentiate. y=5x8Ch. 1 - Differentiate. y=6xCh. 1 - Differentiate. y=x7+3x5+1Ch. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Differentiate. y=(3x21)8Ch. 1 - Differentiate. y=34x4/3+43x3/4Ch. 1 - Prob. 23RECh. 1 - Differentiate. y=(x3+x2+1)5.Ch. 1 - Prob. 25RECh. 1 - Differentiate. y=57x2+1.Ch. 1 - Differentiate. f(x)=1x4.Ch. 1 - Differentiate. f(x)=(2x+1)3Ch. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Differentiate. f(t)=2t3t3.Ch. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - If g(u)=3u1, find g(5) and g(5).Ch. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Find the slope of the graph of y=(3x1)34(3x1)2 at...Ch. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - Prob. 61RECh. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 66RECh. 1 - Height of a Helicopter A helicopter is rising at a...Ch. 1 - Prob. 68RECh. 1 - Prob. 69RECh. 1 - Prob. 70RECh. 1 - Prob. 71RECh. 1 - Prob. 72RECh. 1 - Marginal Cost A manufacturer estimates that the...Ch. 1 - Prob. 74RECh. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - Prob. 83RECh. 1 - Prob. 84RE
Additional Math Textbook Solutions
Find more solutions based on key concepts
Find all solutions of each equation in the interval .
Precalculus: A Unit Circle Approach (3rd Edition)
Testing Hypotheses. In Exercises 13-24, assume that a simple random sample has been selected and test the given...
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
True or False The quotient of two polynomial expressions is a rational expression, (p. A35)
Precalculus
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
Silvia wants to mix a 40% apple juice drink with pure apple juice to make 2 L of a juice drink that is 80% appl...
Beginning and Intermediate Algebra
Is there a relationship between wine consumption and deaths from heart disease? The table gives data from 19 de...
College Algebra Essentials (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 3.12 (B). A horizontal beam AB is 4 m long and of constant flexural rigidity. It is rigidly built-in at the left-hand end A and simply supported on a non-yielding support at the right-hand end B. The beam carries Uniformly distributed vertical loading of 18 kN/m over its whole length, together with a vertical downward load of 10KN at 2.5 m from the end A. Sketch the S.F. and B.M. diagrams for the beam, indicating all main values. Cl. Struct. E.] CS.F. 45,10,376 KN, B.M. 186, +36.15 kNm.7arrow_forwardQize f(x) = x + 2x2 - 2 x² + 4x²² - Solve the equation using Newton Raphsonarrow_forward-b±√√b2-4ac 2a @4x²-12x+9=0 27 de febrero de 2025 -b±√√b2-4ac 2a ⑥2x²-4x-1=0 a = 4 b=-12 c=9 a = 2 b = 9 c = \ x=-42±√(2-4 (4) (9) 2(4)) X = (12) ±√44)-(360) 2(108) x = ±√ X = =±√√²-4(2) (1) 2() X = ±√ + X = X = + X₁ = = X₁ = X₁ = + X₁ = = =arrow_forward
- 3.9 (A/B). A beam ABCDE, with A on the left, is 7 m long and is simply supported at Band E. The lengths of the various portions are AB 1-5m, BC = 1-5m, CD = 1 m and DE : 3 m. There is a uniformly distributed load of 15kN/m between B and a point 2m to the right of B and concentrated loads of 20 KN act at 4 and 0 with one of 50 KN at C. (a) Draw the S.F. diagrams and hence determine the position from A at which the S.F. is zero. (b) Determine the value of the B.M. at this point. (c) Sketch the B.M. diagram approximately to scale, quoting the principal values. [3.32 m, 69.8 KNm, 0, 30, 69.1, 68.1, 0 kNm.]arrow_forward4. Verify that V X (aẢ) = (Va) XẢ + aV X Ả where Ả = xyz(x + y + 2) A and a = 3xy + 4zx by carrying out the detailed differentiations.arrow_forward3. For each of the arrow or quiver graphs shown below, determine analytically V°C and V X Č. From these analytical solutions, identify the extrema (+/-) and plot these points on the arrow graph. (a) C = −✰CosxSiny + ŷSinxCosy -π<ׂу<π Ty (b) C = −xSin2y + ŷCos2y x, y<π -π< (c) C = −xCosx + ŷSiny -π< x, y < πarrow_forward
- 7.10 (B/C). A circular flat plate of diameter 305 mm and thickness 6.35 mm is clamped at the edges and subjected to a Uniform lateral pressure of 345 kN/m². Evaluate: (a) the central deflection, (b) the position and magnitude of the maximum radial stress. C6.1 x 10 m; 149.2 MN/m².] 100 200arrow_forward3.15 (B). A beam ABCD is simply supported at B and C with ABCD=2m; BC 4 m. It carries a point load of 60 KN at the free end A, a Uniformly distributed load of 60 KN/m between B and C and an anticlockwise moment of 80 KN m in the plane of the beam applied at the free end D. Sketch and dimension the S.F. and B.M. diagrams, and determine the position and magnitude of the maximum bending moment. CEL.E.] CS.F. 60, 170, 70KN, B.M. 120, +120.1, +80 kNm, 120.1 kNm at 2.83 m to right of 8.7arrow_forward7.1 (A/B). A Uniform I-section beam has flanges 150 mm wide by 8 mm thick and a web 180 mm wide and 8 mm thick. At a certain section there is a shearing force of 120 KN. Draw a diagram to illustrate the distribution of shear stress across the section as a result of bending. What is the maximum shear stress? [86.7 MN/m².arrow_forward
- 1. Let Ả = −2x + 3y+42, B = - - 7x +lý +22, and C = −1x + 2y + 42. Find (a) Ả X B (b) ẢX B°C c) →→ Ả B X C d) ẢB°C e) ẢX B XC.arrow_forward3.13 (B). A beam ABC, 6 m long, is simply-supported at the left-hand end A and at B I'm from the right-hand end C. The beam is of weight 100 N/metre run. (a) Determine the reactions at A and B. (b) Construct to scales of 20 mm = 1 m and 20 mm = 100 N, the shearing-force diagram for the beam, indicating thereon the principal values. (c) Determine the magnitude and position of the maximum bending moment. (You may, if you so wish, deduce the answers from the shearing force diagram without constructing a full or partial bending-moment diagram.) [C.G.] C240 N, 360 N, 288 Nm, 2.4 m from A.]arrow_forward5. Using parentheses make sense of the expression V · VXVV · Å where Ả = Ã(x, y, z). Is the result a vector or a scaler?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Basic Differentiation Rules For Derivatives; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=IvLpN1G1Ncg;License: Standard YouTube License, CC-BY