Chapter 13, Problem 13.22P

(a)

To determine

Find the factor of safety with respect to sliding for case (a).

Answer to Problem 13.22P

The factor of safety with respect to sliding for case (a) is $\underset{\_}{1.5}$.

Explanation of Solution

Given information:

The bed slope $\left(n^{\prime }\right)$ is 2.

The angle $\left({\varphi }^{\prime }\right)$ of friction is $10°$.

The cohesion $\left(c^{\prime }\right)$ is $33.5{\text{kN/m}}^2$.

The unit weight of the soil $\left(\gamma \right)$ is $17.29{\text{kN/m}}^3$.

The depth (H) of slope is 15.2 m.

Calculation:

Calculate slope angle $\left(\beta \right)$ using the equation:

$\beta ={\tan }^{-1}\left(\frac{1}{n^{\prime }}\right)$

Substitute 2 for $n^{\prime }$.

$\begin{array}{c}\beta ={\tan }^{-1}\left(\frac{1}{2}\right)\\ =26.57°\end{array}$

Assume the developed angle of friction $\left({{\varphi }^{\prime }}_d\right)$ is $5°$.

Find the factor of safety $\left(F_{{\varphi }^{\prime }}\right)$ with respect to friction using the equation:

$F_{{\varphi }^{\prime }}=\frac{\tan {\varphi }^{\prime }}{\tan {{\varphi }^{\prime }}_d}$

Substitute $10°$ for ${\varphi }^{\prime }$ and $5°$ for ${{\varphi }^{\prime }}_d$.

$\begin{array}{c}{F}_{{\varphi }^{\prime }}=\frac{\tan 10°}{\tan 5°}\\ =2.01\end{array}$

Find the Taylor’s stability number (m).

Refer Figure 13.17, “Taylor’s stability number” in the textbook.

Take the value of Taylor’s stability number corresponding friction angle $\left({\varphi }^{\prime }\right)$ of $5°$ and slope angle $\left(\beta \right)$ of $26.57°$

The Taylor’s stability number (m) is 0.098.

Find the developed cohesion $\left({c^{\prime }}_d\right)$ using the equation:

${c^{\prime }}_d=m\gamma H$

Substitute $17.29{\text{kN/m}}^{\text{3}}$ for $\gamma$, 0.098 for m, and 15.2 m for H.

$\begin{array}{c}{c^{\prime }}_d=0.098\times 17.29\times 15.2\\ =25.76{\text{kN/m}}^{\text{2}}\end{array}$

Find the factor of safety with respect to cohesion $\left(F_{c^{\prime }}\right)$ using the equation:

$F_{c^{\prime }}=\frac{c^{\prime }}{{c^{\prime }}_d}$

Substitute $33.5{\text{kN/m}}^{\text{2}}$ for $c^{\prime }$ and $25.76{\text{kN/m}}^{\text{2}}$ for ${c^{\prime }}_d$

$\begin{array}{c}{F}_{c^{\prime }}=\frac{33.5}{25.76}\\ =1.30\end{array}$

Similarly find the factor of safety $\left(F_{{\varphi }^{\prime }}\right)$ with respect to friction, the Taylor’s stability number (m), the developed cohesion $\left({c^{\prime }}_d\right)$, and the factor of safety with respect to cohesion $\left(F_{c^{\prime }}\right)$ for the various assumed value of developed angle of friction $\left({{\varphi }^{\prime }}_d\right)$.

Summarize the values of the factor of safety $\left(F_{{\varphi }^{\prime }}\right)$ with respect to friction, the Taylor’s stability number (m), the developed cohesion $\left({c^{\prime }}_d\right)$, and the factor of safety with respect to cohesion $\left(F_{c^{\prime }}\right)$ as in Table 1.

${{\varphi }^{\prime }}_d\left(\mathrm{deg}\right)$	$F_{{\varphi }^{\prime }}$	m	${c^{\prime }}_d\left({\text{kN/m}}^{\text{2}}\right)$	$F_{c^{\prime }}$
5	2.01	0.098	25.76	1.30
6	1.68	0.090	23.65	1.41
8	1.25	0.078	20.50	1.63
10	1	0.064	16.82	1.99

Plot the graph of factor of safety $\left(F_{{\varphi }^{\prime }}\right)$ with respect to friction and factor of safety with respect to cohesion $\left(F_{c^{\prime }}\right)$ as shown in Figure 1.

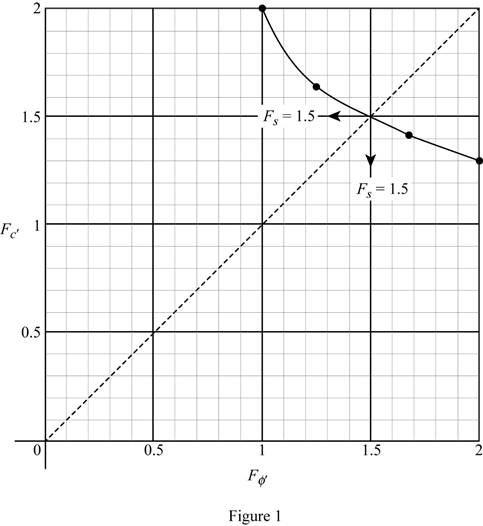
Refer Figure 1.

Find the factor of safety $\left(F_S\right)$ with respect to sliding in case (a).

Draw a line from origin of the graph with an angle of $45°$. It intersects the curve at the coordinate of (1.5, 1.5). The intersection point is the factor of safety with respect to sliding.

Therefore, the factor of safety with respect to sliding for case (a) is $\underset{\_}{1.5}$.

(b)

To determine

Find the factor of safety with respect to sliding for case (b).

Answer to Problem 13.22P

The factor of safety with respect to sliding for case (b) is $\underset{\_}{1.36}$.

Explanation of Solution

Given information:

The bed slope $\left(n^{\prime }\right)$ is 1.0.

The angle $\left({\varphi }^{\prime }\right)$ of friction is $20°$.

The cohesion $\left(c^{\prime }\right)$ is $19.2{\text{kN/m}}^2$.

The unit weight of the soil $\left(\gamma \right)$ is $18.08{\text{kN/m}}^3$.

The depth (H) of slope is 9.15 m.

Calculation:

Calculate slope angle $\left(\beta \right)$ using the equation:

$\beta ={\tan }^{-1}\left(\frac{1}{n^{\prime }}\right)$

Substitute 1 for $n^{\prime }$.

$\begin{array}{c}\beta ={\tan }^{-1}\left(\frac{1}{1}\right)\\ =45°\end{array}$

Assume the developed angle of friction $\left({{\varphi }^{\prime }}_d\right)$ is $5°$.

Find the factor of safety $\left(F_{{\varphi }^{\prime }}\right)$ with respect to friction using the equation:

$F_{{\varphi }^{\prime }}=\frac{\tan {\varphi }^{\prime }}{\tan {{\varphi }^{\prime }}_d}$

Substitute $20°$ for ${\varphi }^{\prime }$ and $5°$ for ${{\varphi }^{\prime }}_d$.

$\begin{array}{c}{F}_{{\varphi }^{\prime }}=\frac{\tan 20°}{\tan 5°}\\ =4.16\end{array}$

Find the Taylor’s stability number (m).

Refer Figure 13.17, “Taylor’s stability number” in the textbook.

Take the value of Taylor’s stability number corresponding friction angle $\left({\varphi }^{\prime }\right)$ of $5°$ and slope angle $\left(\beta \right)$ of $45°$.

The Taylor’s stability number is 0.133.

Find the developed cohesion $\left({c^{\prime }}_d\right)$ using the equation:

${c^{\prime }}_d=m\gamma H$

Substitute $18.08{\text{kN/m}}^{\text{3}}$ for $\gamma$, 0.133 for m, and 9.15 m for H.

$\begin{array}{c}{c^{\prime }}_d=0.133\times 18.08\times 9.15\\ =22.00{\text{kN/m}}^{\text{2}}\end{array}$

Find the factor of safety with respect to cohesion $\left(F_{c^{\prime }}\right)$ using the equation:

$F_{c^{\prime }}=\frac{c^{\prime }}{{c^{\prime }}_d}$

Substitute $19.2{\text{kN/m}}^{\text{2}}$ for $c^{\prime }$ and $22.00{\text{kN/m}}^{\text{2}}$ for ${c^{\prime }}_d$

$\begin{array}{c}{F}_{c^{\prime }}=\frac{19.2}{22.00}\\ =0.87\end{array}$

Similarly find the factor of safety $\left(F_{{\varphi }^{\prime }}\right)$ with respect to friction, the Taylor’s stability number (m), the developed cohesion $\left({c^{\prime }}_d\right)$, and the factor of safety with respect to cohesion $\left(F_{c^{\prime }}\right)$ for the various assumed value of developed angle of friction $\left({{\varphi }^{\prime }}_d\right)$.

Summarize the values of the factor of safety $\left(F_{{\varphi }^{\prime }}\right)$ with respect to friction, the Taylor’s stability number (m), the developed cohesion $\left({c^{\prime }}_d\right)$, and the factor of safety with respect to cohesion $\left(F_{c^{\prime }}\right)$ as in Table 1.

${\varphi }^{\prime }\left(\mathrm{deg}\right)$	$F_{{\varphi }^{\prime }}$	m	${c^{\prime }}_d\left({\text{kN/m}}^{\text{2}}\right)$	$F_{c^{\prime }}$
5	4.16	0.133	22	0.87
10	2.06	0.105	17.37	1.10
15	1.36	0.080	13.23	1.45
20	1	0.058	9.7	2

Plot the graph of factor of safety $\left(F_{{\varphi }^{\prime }}\right)$ with respect to friction and factor of safety with respect to cohesion $\left(F_{c^{\prime }}\right)$ as shown in Figure 1.

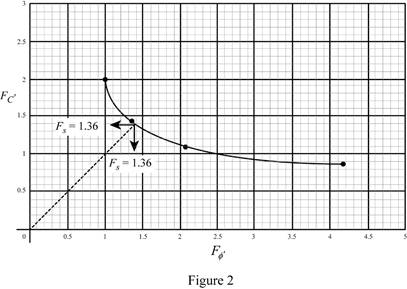
Refer Figure 2.

Find the factor of safety $\left(F_S\right)$ with respect to sliding in case (b).

Draw a line from origin of the graph with an angle of $45°$. It intersects the curve at the coordinate of (1.36, 1.36). The intersection point is the factor of safety with respect to sliding.

Therefore, the factor of safety with respect to sliding for case (b) is $\underset{\_}{1.36}$.