
(a)
Find the factor of safety with respect to sliding for case (a).
(a)
Answer to Problem 13.22P
The factor of safety with respect to sliding for case (a) is
Explanation of Solution
Given information:
The bed slope
The angle
The cohesion
The unit weight of the soil
The depth (H) of slope is 15.2 m.
Calculation:
Calculate slope angle
Substitute 2 for
Assume the developed angle of friction
Find the factor of safety
Substitute
Find the Taylor’s stability number (m).
Refer Figure 13.17, “Taylor’s stability number” in the textbook.
Take the value of Taylor’s stability number corresponding friction angle
The Taylor’s stability number (m) is 0.098.
Find the developed cohesion
Substitute
Find the factor of safety with respect to cohesion
Substitute
Similarly find the factor of safety
Summarize the values of the factor of safety
| m | ||||
| 5 | 2.01 | 0.098 | 25.76 | 1.30 |
| 6 | 1.68 | 0.090 | 23.65 | 1.41 |
| 8 | 1.25 | 0.078 | 20.50 | 1.63 |
| 10 | 1 | 0.064 | 16.82 | 1.99 |
Plot the graph of factor of safety
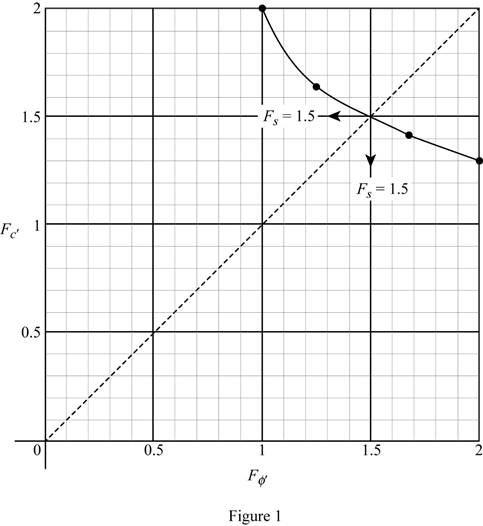
Refer Figure 1.
Find the factor of safety
Draw a line from origin of the graph with an angle of
Therefore, the factor of safety with respect to sliding for case (a) is
(b)
Find the factor of safety with respect to sliding for case (b).
(b)
Answer to Problem 13.22P
The factor of safety with respect to sliding for case (b) is
Explanation of Solution
Given information:
The bed slope
The angle
The cohesion
The unit weight of the soil
The depth (H) of slope is 9.15 m.
Calculation:
Calculate slope angle
Substitute 1 for
Assume the developed angle of friction
Find the factor of safety
Substitute
Find the Taylor’s stability number (m).
Refer Figure 13.17, “Taylor’s stability number” in the textbook.
Take the value of Taylor’s stability number corresponding friction angle
The Taylor’s stability number is 0.133.
Find the developed cohesion
Substitute
Find the factor of safety with respect to cohesion
Substitute
Similarly find the factor of safety
Summarize the values of the factor of safety
| m | ||||
| 5 | 4.16 | 0.133 | 22 | 0.87 |
| 10 | 2.06 | 0.105 | 17.37 | 1.10 |
| 15 | 1.36 | 0.080 | 13.23 | 1.45 |
| 20 | 1 | 0.058 | 9.7 | 2 |
Plot the graph of factor of safety
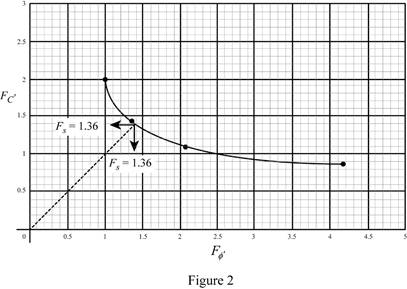
Refer Figure 2.
Find the factor of safety
Draw a line from origin of the graph with an angle of
Therefore, the factor of safety with respect to sliding for case (b) is
Want to see more full solutions like this?
Chapter 13 Solutions
EBK FUNDAMENTALS OF GEOTECHNICAL ENGINE
- Consider the geometric and traffic characteristics shown below. Approach (Width) North South East West (56 ft) (56 ft) (68 ft) (68 ft) Peak hour Approach Volumes: Left Turn 165 105 200 166 Through Movement 447 400 590 543 Right Turn 162 157 191 200 Conflicting Pedestrian Volumes 900 1,200 1,200 900 PHF 0.95 0.95 0.95 0.95 For the following saturation flows: Through lanes: 1,600 veh/h/In Through-right lanes: 1,400 veh/h/In Left lanes: 1,000 veh/h/In Left-through lanes: 1,200 veh/h/In Left-through-right lanes: 1,100 veh/h/In The total cycle length was 283 s. Now assume the saturation flow rates are 10% higher, that is, assume the following saturation flow rates: Through lanes: 1,760 veh/h/In Through-right lanes: 1,540 veh/h/In Left lanes: 1,100 veh/h/In Left-through lanes: 1,320 veh/h/In 1,210 veh/h/In Left-through-right lanes: Determine a suitable signal phasing system and phase lengths (in s) for the intersection using the Webster method. (Enter the sum of green and yellow times for…arrow_forwardThe given beam has continuous lateral support. If the live load is twice the dead load, what is the maximum total service load, in kips / ft, that can be supported? A992 steel is used: Fy = 50 ksi, Fu=65 ksi. Take L = 30 ft. bf For W40 x 149: 2tf = 7.11, = = 54.3, Z 598 in.³ tw W W40 X 149 L (Express your answers to three significant figures.) a. Use LRFD. Wtotal = kips/ft b. Use ASD. Wtotal kips/ftarrow_forwardThe beam shown in the figure below is a W16 × 31 of A992 steel and has continuous lateral support. The two concentrated loads are service live loads. Neglect the weight of the beam and determine whether the beam is adequate. Suppose that P = 52 k. For W16 × 31: d = 15.9 in., tw = 0.275 in., h/tw = 51.6, and M = M₁ = 203 ft-kip, Mn/₁ = Mp/α = 135 ft-kip. P Р W16 x 31 a. Use LRFD. Calculate the required moment strength, the allowable shear strength, and the maximum shear. (Express your answers to three significant figures.) Mu = OvVn = ft-kip kips kips Vu = Beam is -Select- b. Use ASD. Calculate the required moment strength, the allowable shear strength, and the maximum shear. (Express your answers to three significant figures.) Ma = Vn/b - Va = Beam is -Select- ft-kip kips kipsarrow_forward
- Determine the smallest value of yield stress Fy, for which a W-, M-, or S-shape from the list below will become slender. bf/2tfh/tw Shape W12 × 72 8.99 22.6 W12 × 26 8.54 47.2 M4 × 6 11.9 22.0 M12 x 11.8 6.81 62.5 M6 × 4.4 5.39 47.0 S24 × 80 4.02 41.4 S10 × 35 5.03 13.4 (Express your answer to three significant figures.) Fy = ksi To which shape does this value apply? -Select- ✓arrow_forwardCompute the nominal shear strength of an M12 × 11.8 of A572 Grade 60 steel (Fy = 60 ksi). For M12 x 11.8: d = 12 in., tw = 0.177 in., h/tw = 62.5. Vn = kipsarrow_forwardA flexural member is fabricated from two flange plates 1/2 × 71/2 and a web plate 3/8 × 19. The yield stress of the steel is 50 ksi. a. Compute the plastic section modulus Z and the plastic moment Mp with respect to the major principal axis. (Express your answers to three significant figures.) Z = Mp = in. 3 ft-kips b. Compute the elastic section modulus S and the yield moment My with respect to the major principal axis. (Express your answers to three significant figures.) S = My = in.3 ft-kipsarrow_forward
- = 65 ksi. A W16×36 of A992 steel has two holes in each flange for 7/8-inch-diameter bolts. For A992 steel: Fy = 50 ksi, Fu For a W16×36: bƒ = 6.99 in., tƒ = 0.430 in., Z = 64.0 in.³ and Sx = 56.5 in.³ a. Assuming continuous lateral support, verify that the holes must be accounted for and determine the nominal flexural strength. (Express your answer to three significant figures.) Mn = ft-kips b. What is the percent reduction in strength? (Express your answer to three significant figures.) Reduction = %arrow_forwardFind the reinforcements for the mid span and supports for an interior 9 in. thick slab (S-2) in thefloor from Problem 1. Ignore the beams and assume that the slab is supported by columns only (i.e.a flat plate). Sketch the slab and show the reinforcements including the shrinkage andtemperature reinforcement steel. Use f c’ = 4,000 psi and f y = 60,000 psi.NOTE: Problem 3 requires additional column placements at locations such as C and D. The stripof slab between these two columns will behave as a beam support to the one-way slab (with 10 ft.span). Problem 1. The figures below shows the framing plan and section of a reinforced concrete floor system.Floor beams are shown as dotted lines. The weight of the ceiling and floor finishing is 6 psf,that of the mechanical and electrical systems is 7 psf, and the weight of the partitions is 180psf. The floor live load is 105 psf. The 7 in. thick slab exterior bay (S-1) is reinforced with #5rebars @ 10 in. o.c. as the main positive…arrow_forward1- A study of freeway flow at a particular site has resulted in a calibrated speed-density relationship, as follows u = 57.5(10.008k) a) Find the free-flow speed and jam density b) Derive the equations describing flow versus speed and flow versus density c) Determine the capacity of the road 2- A rural freeway has a demand volume of 6750 v/hr. It has four 3.4 m lanes in each direction. The traffic stream is comprised of 8% heavy vehicles and a PHF of 0.94. The terrain is rolling throughout the segment. What is the level of service for the facility? What is the capacity? 3- For an urban freeway, how many 3.6 m lanes in each direction are needed to achieve LOS C on a freeway with a peak hour traffic volume of 5725 v/hr and with a PHF = 0.967 The traffic stream is comprised of 11% heavy vehicles and the location is level terrain.arrow_forward
- Note: Provide a clear, step-by-step simplified handwritten solution (with no extra explanations) that is entirely produced by hand without any AI help. I require an expert-level answer, and I will assess it based on the quality and accuracy of the work, referring to the attached image for additional guidance. Make sure every detail is carefully verified for correctness before you submit. Thanks!.arrow_forwardExample 3 Design a rectangular reinforced concrete beam having a 6 m simple span. A service dead load of 25 kN/m (not including the beam weight) and a service live load 10kn/m are to be supported. use f'c = 25 MPa and fy = 420MPaarrow_forwardNote:arrow_forward
 Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning
Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning



