
Concept explainers
Calculate the volume of a sphere that is circumscribed about the cube.
Answer to Problem 45HP
The volume of the sphere is
Explanation of Solution
Given:
It is given in the question that a cube has a volume of
Concept Used:
In this, use the concept of Pythagoras theorem, volume of cube and volume of sphere i.e.
Calculation: Here,
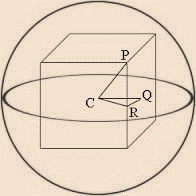
Since a circumscribed sphere will only intersect the cube at its vertices. The center of the sphere is the center of the cube.
CQ = QR= RP = 3 because they are half of the side of the cube. Using Pythagoras theorem, to find CR.
Again using the Pythagoras theorem to find CP , the radius of the
Now, the volume of the sphere is
Conclusion:
The volume is
Chapter 12 Solutions
Glencoe Geometry
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Introductory Statistics
University Calculus: Early Transcendentals (4th Edition)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
- 39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forwardA parallelogram with an area of 211.41 m^2 hast a base Thatcher measures 24.3m. Find ist height.arrow_forwardBH is tangent to circle A and DF is a diameter. I don't know where to go from here. May you help please?arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

