
To find the area of each shaded region.
Answer to Problem 50SR
Explanation of Solution
Given:
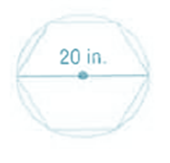
Diameter
Hexagon
Formula used:
Area of a circle
Area of a hexagon
Calculation:
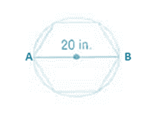
From the figure,
Now for the area of circle,
Putting the value of
So, area of the circle
Now for the area of hexagon,
Radius of the circle
Area of the hexagon
Not putting the value of
So, area of the shaded region
Hence, area of the shaded region
Conclusion:
Therefore, the area of the shaded region in the given figure is
Chapter 12 Solutions
Glencoe Geometry
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
A First Course in Probability (10th Edition)
Elementary Statistics (13th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Introductory Statistics
Pre-Algebra Student Edition
- 39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forwardA parallelogram with an area of 211.41 m^2 hast a base Thatcher measures 24.3m. Find ist height.arrow_forwardBH is tangent to circle A and DF is a diameter. I don't know where to go from here. May you help please?arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

