
Chebyshev’s Theorem How can you determine whether a distribution is approximately normal? A statistical theorem called Chebyshev’s theorem states that the minimum percent of data between plus and minus K standard deviations from the mean (K > 1) in any distribution can be found by the formula
Minimum percent =
Thus, for example, between ±2 standard deviations from the mean there will always be a minimum of 75% of data. This minimum percent applies to any distribution For K = 2,
Minimum percent
Likewise, between ±3 standard deviations from the mean there will always be a minimum of 89% of the data. For K = 3,
Minimum percent
The following table lists the minimum percent of data in any distribution and the actual percent of data in the normal distribution between ±1.1, ± 1.5, ± 2.0, and ±2.5 standard deviations from the mean. The minimum percents of data m any distribution were calculated by using Chebyshev’s theorem. The actual percents of data for the normal distribution were calculated by using the area given in the standard normal, or z, table.
| K = 1.1 | K = 1.5 | K = 2 | K = 2.5 | |
| Minimum (for any distribution) | 17.4% | 55.6% | 75% | 84% |
| Normal distribution | 72.9% | 86.6% | 95.4% | 98.8% |
| Given distribution |
The third row of the chart has been left blank for you to fill in the percents when you reach part (e).
Consider the following 30 pieces of data obtained from a quiz.
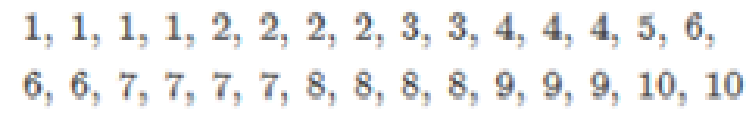
- a. Determine the mean of the set of scores.
- b. Determine the standard deviation of the set of scores.
- c. Determine the values that correspond to 1.1, 1.5, 2, and 2.5 standard deviations above the mean. Then determine the values that correspond to 1.1, 1.5, 2, and 2. 5 standard deviations below the mean.
- d. By observing the 30 pieces of data, determine the actual percent of quiz scores between
±1.1 standard deviations from the mean.
±1.5 standard deviations from the mean.
±2 tandard deviations from the mean.
±2.5 standard deviations from the mean.
- e. Place the percents found in part (d) in the third row of the chart.
- f. Compare the percents in the third row of the chart with the minimum percents in the first row and the normal percents in the second row, and then make a judgment as to whether this set of 30 scores is approximately
normally distributed .
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
EBK SURVEY OF MATHEMATICS WITH APPLICAT
- 3. Let sin (22) + cos (T2) f(z) = z(22 + 1)(z+1) Compute f(z)dz over each of the contours/closed curves C1, C2, C3 and C4 shown below. L 10 -C x Don't use any Al tool show ur answer pe n and paper then takearrow_forwardwhat is the slope of the linear equation-5x+2y-10=0arrow_forward1. Evaluate (2,5) (3x+y)dx+(2y-x)dy (0,1) (i) along the straight lines from (0, 1) to (2, 1) and then from (2, 1) to (2,5), and (ii) along the parabola y = x² + 1. Don't use any Al tool show ur answer in pe n and paper then takearrow_forward
- Don't use any Al tool show ur answer in pe n and paper then take 20. Solve the given system of differential equations: x' = x+y, x(0) = 0 y' = 2x, y(0) = 1arrow_forward4. Verify the Cauchy-Goursat theorem for the function f(z) =225z around the closed curve C defined by a half circle || = 1 from the point (1,0) to (-1, 0) in the counterclockwise direction and then the straight line from (-1,0) to (1,0). Don't use any Al tool show ur answer in pe n and paper then takearrow_forward2. Evaluate the following integral using cauchy integral theorem: ||=3 sin (22)+cos (22) (2-1)(2-2) -dz Don't use any Al tool show ur answer in pe n and paper then takearrow_forward
- 18. Solve the given differential equation: y' + y = f(t), y(0) = 5, where f(t) = 0arrow_forward16. Solve the given differential equation: y" + 4y Given, = sin (t)u(t2), y(0) = 1, y'(0) = 0 1 = (x² + 1)(x²+4) 1/3 -1/3 + x²+1 x²+4 Don't use any Al tool show ur answer in pe n and paper then takearrow_forwardHow to solve and explain (7x^2 -10x +11)-(9x^2 -4x + 6)arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt

