Chapter 12.3, Problem 9E

To determine

(a)

To find:

The sum of squared errors, SSE.

Answer to Problem 9E

Solution:

The equation of the least squares regression line is $\widehat{y}=908.07+313.98x$ and the sum of

Squared error (SSE) is $1148767.96$.

Explanation of Solution

Given Information:

The numbers of parking tickets students received during one semester and their monthly

Parking Tickets and Monthly Income
Number of Tickets,	10	8	3	2	0	5	4	2	1	0
Monthly Income (in Dollars),	4000	3800	1500	2000	870	2500		1800	1200	1400

The least Squares regression line is the line for which the average variation from the data is the smallest, also called the line of best fit, given by $\widehat{y}=b_0+b_{1}x$.

Where is the slope of the least-squares regression line for paired data from a sample and is the -intercept for the regression line.

The sum of squared errors (SSE) for a regression line is the sum of the squares of the residuals.

Formula used:

The equation of least-squares regression line is given by

$\widehat{y}=b_0+b_{1}x$

Where, is the slope of the least-squares regression line given as,

$b_1=\frac{n{\displaystyle \sum x_i{y}_i-\left({\displaystyle \sum x_i}\right)\left({\displaystyle \sum y_i}\right)}}{n{\displaystyle \sum x_i{}^2}-{\left({\displaystyle \sum x_i}\right)}^2}$ and $b_0$ is intercept given as,

$b_0=\frac{{\displaystyle \sum y_i}}{n}-b_1\frac{{\displaystyle \sum x_i}}{n}$

Here n is the number of data pairs in the sample, is the value of the explanatory variable and is the value of response variable.

The sum of squared errors (SSE) for a regression line is the sum of the squares of the residuals is given by,

$\text{SSE}={{\displaystyle \sum \left(y_i-\widehat{y}\right)}}^2$

Here is the observed value of the response variable and is the predicted variable of using the list square regression model.

Calculation:

The table of the numbers of parking tickets students received during one semester and

their monthly Incomes is given by,

Number of Tickets, $x_i$	Monthly Income (in Dollars), $y_i$	$x_i{y}_i$	$x_i^2$	$y_i^2$
10	4000	40000	100	16000000
8	3800	30400	64	14440000
3	1500	4500	9	2250000
2	2000	4000	4	4000000
0	870	0	0	756900
5	2500	12500	25	6250000
4	1800	7200	16	3240000
2	1000	2000	4	1000000
1	1200	1200	1	1440000
0	1400	0	0	1960000
${\displaystyle \sum x_i}=35$	${\displaystyle \sum y_i}=20,070$	${{\displaystyle \sum x_{i}y}}_i=101,800$	${\displaystyle \sum x_i^2}=223$	${\displaystyle \sum y_i^2}=51,336,900$

Where, ${\displaystyle \sum x_i}=x_1+x_2+x_3+\mathrm{...}+x_{10}$.

Substitute 10 for, 8 for, 3 for… 0 for in the above equation,

$\begin{array}{rll}{\displaystyle \sum x_i}& =& 10+8+3+\mathrm{...}+0\\ & =& 35\end{array}$

${\displaystyle \sum y_i}=y_1+y_2+y_3+\mathrm{...}+y_{10}$

Substitute for, for, for… for in the above equation,

$\begin{array}{rll}{\displaystyle \sum y_i}& =& 4000+3800+1500+\mathrm{...}+1400\\ & =& 20,070\end{array}$

In order to calculate the value of $x_i{y}_i$, substitute 10 for and 4000 for in $x_i{y}_i$.

$\begin{array}{rll}{x}_i{y}_i& =& \left(10\right)\left(4000\right)\\ & =& 40000\end{array}$

Proceed in the same manner to calculate $x_i{y}_i$ for the rest of the data and refer table for the rest of the $x_i{y}_i$ values calculated.

$\begin{array}{rll}{\displaystyle \sum x_i{y}_i}& =& 40000+30400+4500+\mathrm{...}+0\\ & =& 101,800\end{array}$

In order to calculate the value of, substitute 10 for in.

$\begin{array}{l}{{{\displaystyle x}}_i}^2=(10)(10)\\ =100\end{array}$

Proceed in the same manner to calculate for the rest of the data and refer table for the rest of the values calculated.

$\begin{array}{l}{\displaystyle \sum {{{\displaystyle x}}_i}^2=100+64+9+\mathrm{...}+0}\\ =223\end{array}$

In order to calculate the value of substitute 4000 for in .

$\begin{array}{l}{{{\displaystyle y}}_i}^2=(4000)(4000)\\ =16000000\end{array}$

Proceed in the same manner to calculate for the rest of the data and refer table for the rest of the values calculated.

$\begin{array}{l}{\displaystyle \sum {{{\displaystyle y}}_i}^2=16000000+14400000+2250000+\mathrm{...}+1960000}\\ =51,336,900\end{array}$

The slope of the least-squares regression line is given as,

$b_1=\frac{n{\displaystyle \sum {{\displaystyle x}}_i{{\displaystyle y}}_i-\left({\displaystyle \sum {{\displaystyle x}}_i}\right)\left({\displaystyle \sum {{\displaystyle y}}_i}\right)}}{n{\displaystyle \sum {{{\displaystyle x}}_i}^2-{\left({\displaystyle \sum {{{\displaystyle x}}_i}^2}\right)}^2}}$

Substitute 35 for ${\displaystyle \sum {{\displaystyle x}}_i}$, 20, 070 for ${\displaystyle \sum {{\displaystyle y}}_i}$, 101, 800 for ${\displaystyle \sum {{\displaystyle x}}_i}{y}_i$, 223 for ${{\displaystyle \sum {{\displaystyle x}}_i}}^2$ and 51, 336, 900 for in the above equation of,

$\begin{array}{l}{b}_1=\frac{10(101,800)-\left(35\right)(20,070)}{10(223)-{(35)}^2}\\ =\frac{315550}{1005}\\ =313.98\end{array}$

The -intercept of regression line is given as,

$b_0=\frac{{\displaystyle \sum {{\displaystyle y}}_i}}{n}-b_1\frac{{\displaystyle \sum {{\displaystyle x}}_i}}{n}$

Substitute 35 for ${\displaystyle \sum {{\displaystyle x}}_i}$, 20, 070 for ${\displaystyle \sum {{\displaystyle y}}_i}$ and 313.98 for $b_0$

$\begin{array}{l}{b}_0=\frac{20,070}{10}-(313.987)\frac{35}{10}\\ =2007-1098.93\\ =908.07\end{array}$

The equation of least-squares regression line is,

$\widehat{y}=908.07+313.98x$

The table of the numbers of parking tickets students received during one semester and

their monthly incomes is given by,

Number of Tickets, $x_i$	Monthly Income (in Dollars), $y_i$	Predicted value, $y_i$	Residual, $(y_i-\widehat{y_i})$	Squared error, ${(y_i-\widehat{y_i})}^2$
10	4000	4047.87	-47.87	2291.5369
8	3800	3419.91	380.09	144468.4081
3	1500	1850.01	-350.01	122507.0001
2	2000	1536.03	463.97	215268.1609
0	870	908.07	-38.07	1449.3249
5	2500	2477.97	22.03	485.3209
4	1800	2163.99	-363.99	132488.7201
2	1000	1536.03	-536.03	287328.1609
1	1200	1222.05	-22.05	486.2025
0	1400	908.07	491.93	241995.1249
${\displaystyle \sum {{\displaystyle x}}_i}=35$	${\displaystyle \sum {{\displaystyle y}}_i}=20,070$	${\displaystyle \sum \widehat{{{\displaystyle y}}_i}}=20,070$	${\displaystyle \sum (y_i-\widehat{y_i})=0}$	${\displaystyle \sum {(y_i-\widehat{y_i})}^2=1148767.96}$

The predicted values are obtained by substituting the values of in the fitted regression line,

$\widehat{y}=908.07+313.98x$

For, substitute 10 for in the above equation,

$\begin{array}{l}\widehat{y}=908.07+313.98x\\ =908.07+313.98(10)\\ =4047.87\end{array}$

Similarly the other values of are obtained and are shown in the third column of the table:

The residuals $(y_i-\widehat{y_i})$ in column four of the table are obtained by the difference of valued of and .

Substitute 4000 for and 4047.87 for in above equation,

$\begin{array}{l}(y_i-\widehat{y_i})=4000-4047.87\\ =-47.87\end{array}$

Similarly the other values of $(y_i-\widehat{y_i})$ are obtained and are shown in the fourth column of the table.

The squared errors are obtained as, ${(y_i-\widehat{y_i})}^2$

Substitute for in $(y_i-\widehat{y_i})$,

Thus, $(y_i-\widehat{y_i})=2291.5369$

Similarly the other values of ${(y_i-\widehat{y_i})}^2$ are obtained and are shown in the last column of the table.

The sum of squared errors (SSE) for a regression line is,

$SSE={{\displaystyle \sum (y_i-\widehat{y_i})}}^2$

From the above table SSE is given by,

$\begin{array}{l}{{\displaystyle \sum (y_i-\widehat{y_i})}}^2=2291.5369+144468.4081+\mathrm{...}+241995.12489\\ =1148767.96\end{array}$

Thus, the sum of squared error (SSE) is 114767.96.

Conclusion:

The equation of least-squares regression line is,

$\widehat{y}=908.07+313.98x$

The sum of squared errors (SSE) is 1148767.96.

To determine

(b)

To find:

The Standard error of estimate, .

Answer to Problem 9E

Solution:

The Standard error of estimate is 378.94.

Explanation of Solution

Given Information:

The numbers of parking tickets students received during one semester and their monthly

Parking Tickets and Monthly Income
Number of Tickets,	10	8	3	2	0	5	4	2	1	0
Monthly Income (in Dollars),	4000	3800	1500	2000	870	2500	1800	1000	1200	1400

Incomes is,

Formula used:

The standard error of estimate is a measure of the deviation of the sample data points from the regression line and is given by:

$\begin{array}{l}{S}_e=\sqrt{\frac{{\displaystyle \sum {(y_i-\widehat{y_i})}^2}}{n-2}}\\ =\sqrt{\frac{SSE}{n-2}}\end{array}$

Here SSE is the sum of squared error and is the number of paired data set in the sample, is the observed value of the response variable,

is the predicted variable of using the list square regression model.

Calculation:

The formula of Standard error of estimate is,

$\begin{array}{l}{S}_e=\sqrt{\frac{{\displaystyle \sum {(y_i-\widehat{y_i})}^2}}{n-2}}\\ =\sqrt{\frac{SSE}{n-2}}\end{array}$

From part a substitute for SSE and for in the above equation of Standard error of estimate.

$\begin{array}{l}{S}_e=\sqrt{\frac{1148767.96}{10-2}}\\ =\sqrt{143595.995}\\ =378.94\end{array}$

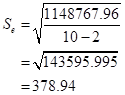
Conclusion:

Thus, the Standard error of estimate is 378.94.

To determine

(c)

To Construct:

A 95% prediction interval for the given value of explanatory variable, .

Answer to Problem 9E

Solution:

The prediction interval is (2032.14, 3551.76).

Explanation of Solution

The prediction interval is a confidence interval for an individual value of the response

Variable y, at a given fixed value of the explanatory variable, x.

Formula used:

The formula to calculate the margin of error of a prediction interval for an individual value of the response variable, y, is given by,

$E=t_{\alpha /2}{S}_e\sqrt{1+\frac{1}{n}+\frac{n{\left(x_0-\overline{x}\right)}^2}{n\left({\displaystyle \sum x_i^2}\right)-{\left({\displaystyle \sum x_i}\right)}^2}}$.

$S_e$ is the Standard error of estimate,.

n is the number of data pairs in the sample.

$x_0$ is the fixed value of the explanatory variable, x.

$\overline{x}$ is the mean of the $x$-values for the data points in the sample.

$x_i$ is the $i^{th}$ value of the explanatory variable.

The formula to calculate the Prediction interval is given by,

$\widehat{y}-E<Y<\widehat{y}+E$

or

$\left(\widehat{y}-E,\widehat{y}+E\right)$.

Where $\widehat{y}$ is the predicted value of the response variable, y, when $x=x_0$ and $E$ is the

margin of error

The formula to calculate arithmetic mean is given by,

$\overline{x}=\frac{x_1+x_2+\mathrm{.....}+x_n}{n}$

Where $x_1$, $x_2$,…. $x_n$ are explanatory variables and $n$ is the total number of explanatory

Variables.

Calculation:

Arithmetic Mean is given as,

$\overline{x}=\frac{x_1+x_2+\mathrm{.....}+x_n}{n}$

From part a substitute 10 for, 10 for, 8 for …..0 for in the above equation of arithmetic mean,

$\begin{array}{l}\overline{x}=\frac{10+8+\mathrm{..}+0}{10}\\ =\frac{35}{10}\\ =3.5\end{array}$

Since the level of confidence is 95%,

$\begin{array}{rll}\alpha & =& 1-0.95\\ & =& 0.05\end{array}$

Then using the t-distribution table, the critical value for this test

$\begin{array}{rll}{t}_{\alpha /2}& =& t_{0.05/2}\\ & =& t_{0.025}\end{array}$

For -distribution with 8 degrees of freedom,

$t_{0.025}=1.86$

The formula to calculate the margin of error of a prediction interval is,

$E=t_{\alpha /2}{S}_e\sqrt{1+\frac{1}{n}+\frac{n{\left(x_0-\overline{x}\right)}^2}{n\left({\displaystyle \sum x_i^2}\right)-{\left({\displaystyle \sum x_i}\right)}^2}}$

Substitute 1.86 for, 3.5 for, 10 for, 35 for, 223 for, 6 for and for in the above equation of margin of error,

$\begin{array}{rll}E& =& \left(1.86\right)\left(378.94\right)\sqrt{1+\frac{1}{10}+\frac{10{\left(6-3.5\right)}^2}{10(223)-{(35)}^2}}\\ & =& 759.81\end{array}$

Predicted value for is

$\begin{array}{l}\widehat{y}=908.07+313.98x\\ =908.07+313.98(6)\\ =2791.95\end{array}$

The prediction interval is:

$\left(\widehat{y}-E,\widehat{y}+E\right)$

Substitute 2791.95for and 759.81 for in the above formula,

$\begin{array}{l}predictioninterval=(2791.95-759.81,2791.95+759.81)\\ =(2032.14,3551.76)\end{array}$

The prediction interval is $(2032.14,3551.76)$.

Conclusion:

Thus, the prediction interval is $(2032.14,3551.76)$.

To determine

(d)

To Construct:

A 95% confidence interval for the intercept of regression line.

Answer to Problem 9E

Solution:

The 95% confidence interval for the intercept is (496.45, 1319.69).

Explanation of Solution

Given Information:

The numbers of parking tickets students received during one semester and their monthly

Incomes is,

Parking Tickets and Monthly Income
Number of Tickets, x	10	8	3	2	0	5	4	2	1	0
Monthly Income	4000	3800	1500	2000	870	2500	1800	1000	1200	1400
(in Dollars), y

Calculation:

To generate the regression table in excel follow the given steps:

1. Under data tab, choose data analytics and then select regression.

2. Select the input Y range and enter the range of the given and select the input X range and enter the range of the given data.

3.Choose 95% confidence interval and click OK.

The following table will appear.

SUMMARY OUTPUT

Regression Statistics
Multiple R	0.94662523
R Square	0.89609937
Adjusted R Square	0.88311172
Standard Error	378.940622
Observations	10
ANOVA
	df	SS	MS	F	Significance F
Regression	1	9907642.04	9907642	68.99665	3.32835E-05
Residual	8	1148767.96	143596
Total	9	11056410

	Coefficients	Standard Error	t Stat	P-value	Lower 95.0%	Upper 95.0%
Intercept	908.0696517	178.5009634	5.087197	0.000945	496.4456924	1319.69361
X	313.9800995	37.79968083	8.306422	3.33E-05	226.8138793	401.14632

From the above result,

1. Multiple R is the absolute value of the Correlation Coefficient, .

2. $R^2$ is the Coefficient of determination, $r^2$.

3. Standard Error is the standard error of the estimate, .

4. The intersection of the Residual row and the SS column is the sum of squared errors, SSE.

5. The Lower 95.0% and the Upper 95.0% columns give the lower and upper endpoints of the 95% confidence intervals for the intercept and slope.

6. The coefficient columns gives the values for the coefficients, that is, the

intercept and slope, of the regression line.

The row labeled Intercept is the row for the values corresponding to the intercept. The last two values in this row are the lower and upper endpoints for a 95% confidence for the intercept of the regression line, ${\beta }_0$.

Thus, the 95% confidence interval for ${\beta }_0$ is,

$496.45<{\beta }_0<1319.69$

Confidence Interval=(496.45, 1319.69).

Conclusion:

Thus, the 95% confidence interval for the intercept is(496.45, 1319.69).

To determine

(e)

To Construct:

A 95% confidence interval for the slope of regression line.

Answer to Problem 9E

Solution:

Thus, the 95% confidence interval for the slope ${\beta }_1$ is(226.81, 401.15).

Explanation of Solution

Given Information:

The numbers of parking tickets students received during one semester and their monthly

Incomes is,

Parking Tickets and Monthly Income
Number of Tickets, x	10	8	3	2	0	5	4	2	1	0
Monthly Income	4000	3800	1500	2000	870	2500	1800	1000	1200	1400
(in Dollars), y

Calculation:

To generate the regression table in excel follow the given steps:

1. Under data tab, choose data analytics and then select regression.

2. Select the input Y range and enter the range of the given and select the input X range and enter the range of the given data.

3.Choose 95% confidence interval and click OK.

The following table will appear.

SUMMARY OUTPUT

Regression Statistics
Multiple R	0.946625253
R Square	0.89609937
Adjusted R Square	0.883111792
Standard Error	378.940622
Observations	10
ANOVA
	df	SS		MS	F	Significance F
Regression	1	9907642.04		9907642	68.99665	3.32835E-05
Residual	8	1148767.96		143596
Total	9	11056410

	Coefficients	Standard Error	t Stat	P-value	Lower 95.0%	Upper 95.0%
Intercept	908.0696517	178.5009634	5.087197	0.000945	496.4456924	1319.69361
X	313.9800995	37.79968083	8.306422	3.33E-05	226.8138793	401.14632

From the above result,

1. Multiple R is the absolute value of the Correlation Coefficient, .

2. $R^2$ is the Coefficient of determination, $r^2$.

3. Standard Error is the standard error of the estimate, .

4. The intersection of the Residual row and the SS column is the sum of squared errors, SSE.

5. The Lower 95.0% and the Upper 95.0% columns give the lower and upper endpoints of the 95% confidence intervals for the intercept and slope.

6. The coefficient columns gives the values for the coefficients, that is, the

intercept and slope, of the regression line.

The row labeled is the row for the values corresponding to the slope of regression line. The last two values in this row are the lower and upper endpoints for a 95% confidence for the slope of the regression line, ${\beta }_1$.

Thus, the 95% confidence interval for ${\beta }_1$ is,

$226.81<{\beta }_1<401.15$

Confidence Interval=(226.81, 401.15).

Conclusion:

Thus, the 95% confidence interval for the slope is(226.81, 401.15).