Calculus & Its Applications
12th Edition
ISBN: 9780137590810
Author: Larry J. Goldstein, David C. Lay, David I. Schneider, Nakhle H. Asmar, William Edward Tavernetti
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 12.2, Problem 27E
An experiment consists of selecting a point at random from the region inside the square in Fig.10(a). Let
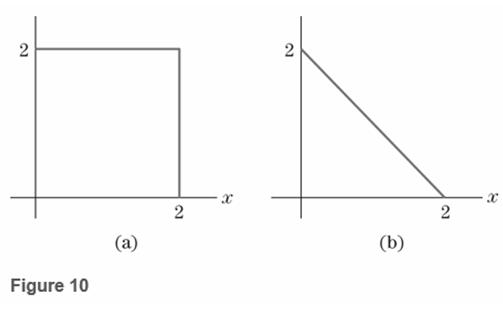
Show that the cumulative distribution function of
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Only 100% sure experts solve it correct complete solutions ok
rmine the immediate settlement for points A and B shown in
figure below knowing that Aq,-200kN/m², E-20000kN/m², u=0.5, Depth
of foundation (DF-0), thickness of layer below footing (H)=20m.
4m
B
2m
2m
A
2m
+
2m
4m
sy = f(x)
+
+
+
+
+
+
+
+
+
X
3
4
5
7
8
9
The function of shown in the figure is continuous on the closed interval [0, 9] and differentiable on the open
interval (0, 9). Which of the following points satisfies conclusions of both the Intermediate Value Theorem
and the Mean Value Theorem for f on the closed interval [0, 9] ?
(A
A
B
B
C
D
Chapter 12 Solutions
Calculus & Its Applications
Ch. 12.1 - Compute the expected value and the variance of the...Ch. 12.1 - Prob. 2CYUCh. 12.1 - Prob. 1ECh. 12.1 - Prob. 2ECh. 12.1 - Prob. 3ECh. 12.1 - Prob. 4ECh. 12.1 - Prob. 5ECh. 12.1 - Probability Table, Expected Value The number of...Ch. 12.1 - Prob. 7ECh. 12.1 - Prob. 8E
Ch. 12.1 - Decision Making Based on Expected Value A citrus...Ch. 12.1 - Prob. 10ECh. 12.2 - Prob. 1CYUCh. 12.2 - Prob. 2CYUCh. 12.2 - Prob. 1ECh. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Prob. 6ECh. 12.2 - Prob. 7ECh. 12.2 - Prob. 8ECh. 12.2 - Prob. 9ECh. 12.2 - Prob. 10ECh. 12.2 - Prob. 11ECh. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.2 - Prob. 18ECh. 12.2 - Prob. 19ECh. 12.2 - Prob. 20ECh. 12.2 - Prob. 21ECh. 12.2 - Prob. 22ECh. 12.2 - Prob. 23ECh. 12.2 - Prob. 24ECh. 12.2 - Prob. 25ECh. 12.2 - Prob. 26ECh. 12.2 - An experiment consists of selecting a point at...Ch. 12.2 - Prob. 28ECh. 12.2 - Prob. 29ECh. 12.2 - Prob. 30ECh. 12.2 - Prob. 31ECh. 12.2 - Prob. 32ECh. 12.2 - Prob. 33ECh. 12.2 - Prob. 34ECh. 12.2 - Prob. 35ECh. 12.2 - A random variable X has a cumulative distribution...Ch. 12.2 - Prob. 37ECh. 12.2 - Prob. 38ECh. 12.3 - Prob. 1CYUCh. 12.3 - Prob. 2CYUCh. 12.3 - Prob. 1ECh. 12.3 - Prob. 2ECh. 12.3 - Prob. 3ECh. 12.3 - Prob. 4ECh. 12.3 - Prob. 5ECh. 12.3 - Prob. 6ECh. 12.3 - Prob. 7ECh. 12.3 - Prob. 8ECh. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - Prob. 12ECh. 12.3 - Expected Reading Time The amount oftime (in...Ch. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - Prob. 17ECh. 12.3 - Prob. 18ECh. 12.3 - If X is a random variable with density function...Ch. 12.3 - Prob. 20ECh. 12.3 - Prob. 21ECh. 12.3 - Prob. 22ECh. 12.3 - Prob. 23ECh. 12.3 - Prob. 24ECh. 12.3 - Prob. 25ECh. 12.3 - Prob. 26ECh. 12.4 - The emergency flasher on an automobile is...Ch. 12.4 - Prob. 2CYUCh. 12.4 - Prob. 1ECh. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Prob. 4ECh. 12.4 - Prob. 5ECh. 12.4 - In a large factory there is an average of two...Ch. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - During a certain part of the day, the time between...Ch. 12.4 - During a certain part of the day, the time between...Ch. 12.4 - Prob. 11ECh. 12.4 - Prob. 12ECh. 12.4 - Reliability of Electronic Components Suppose that...Ch. 12.4 - Prob. 14ECh. 12.4 - Prob. 15ECh. 12.4 - Find the expected values and the standard...Ch. 12.4 - Prob. 17ECh. 12.4 - Find the expected values and the standard...Ch. 12.4 - Prob. 19ECh. 12.4 - Prob. 20ECh. 12.4 - Prob. 21ECh. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - Prob. 25ECh. 12.4 - Normal Distribution and Life of a Tire Suppose...Ch. 12.4 - Amount of Milk in a Container If the amount of...Ch. 12.4 - Breaking weight Theamount of weight required to...Ch. 12.4 - Time of a commute A student with an eight oclock...Ch. 12.4 - Prob. 30ECh. 12.4 - Diameter of a Bolt A certain type of bolt must fit...Ch. 12.4 - Prob. 32ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 34ECh. 12.4 - Prob. 35ECh. 12.4 - Prob. 36ECh. 12.4 - Prob. 37ECh. 12.5 - A public health officer is tracking down the...Ch. 12.5 - Suppose that a random variable X has a Poisson...Ch. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - Prob. 4ECh. 12.5 - Number of Insurance Claims The monthly number of...Ch. 12.5 - Waiting Time in an Emergency Room On a typical...Ch. 12.5 - Prob. 7ECh. 12.5 - Number of Cars at a Tollgate During a certain part...Ch. 12.5 - Poisson Distribution in a Mixing Problem A bakery...Ch. 12.5 - Prob. 10ECh. 12.5 - Prob. 11ECh. 12.5 - Quality Control The quality-control department at...Ch. 12.5 - Two Competing Companies In a certain town, there...Ch. 12.5 - Prob. 14ECh. 12.5 - Prob. 15ECh. 12.5 - Prob. 16ECh. 12.5 - Prob. 17ECh. 12.5 - Prob. 18ECh. 12.5 - Prob. 19ECh. 12.5 - Prob. 20ECh. 12.5 - Prob. 21ECh. 12.5 - Prob. 22ECh. 12.5 - Prob. 23ECh. 12.5 - Prob. 24ECh. 12.5 - Prob. 25ECh. 12.5 - The number of accidents occurring each month at a...Ch. 12 - What is probability table?Ch. 12 - Prob. 2FCCECh. 12 - Prob. 3FCCECh. 12 - Prob. 4FCCECh. 12 - Prob. 5FCCECh. 12 - Prob. 6FCCECh. 12 - Prob. 7FCCECh. 12 - Prob. 8FCCECh. 12 - Prob. 9FCCECh. 12 - Give two ways to compute the variance of a...Ch. 12 - Prob. 11FCCECh. 12 - Prob. 12FCCECh. 12 - Prob. 13FCCECh. 12 - Prob. 14FCCECh. 12 - How is an integral involving a normal density...Ch. 12 - Prob. 16FCCECh. 12 - Prob. 17FCCECh. 12 - Let X be a continuous random variable on 0x2, with...Ch. 12 - Prob. 2RECh. 12 - Prob. 3RECh. 12 - Prob. 4RECh. 12 - Prob. 5RECh. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Probability of Gasoline Sales A certain gas...Ch. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Prob. 15RECh. 12 - Prob. 16RECh. 12 - Prob. 17RECh. 12 - Deciding on a Service Contract The condenser motor...Ch. 12 - Prob. 19RECh. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RECh. 12 - Area under the Normal Curve It is useful in some...Ch. 12 - Prob. 28RECh. 12 - Prob. 29RECh. 12 - Prob. 30RECh. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Rolling Dice A pair of dice is rolled until a 7 or...Ch. 12 - Rolling Dice A pair of dice is rolled until a 7 or...Ch. 12 - Rolling Dice A pair of dice is rolled until a 7 or...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- = Q6 What will be the allowable bearing capacity of sand having p = 37° and ydry 19 kN/m³ for (i) 1.5 m strip foundation (ii) 1.5 m x 1.5 m square footing and (iii)1.5m x 2m rectangular footing. The footings are placed at a depth of 1.5 m below ground level. Assume F, = 2.5. Use Terzaghi's equations. 0 Ne Na Ny 35 57.8 41.4 42.4 40 95.7 81.3 100.4arrow_forwardQ1 The SPT records versus depth are given in table below. Find qan for the raft 12% foundation with BxB-10x10m and depth of raft D-2m, the allowable settlement is 50mm. Elevation, m 0.5 2 2 6.5 9.5 13 18 25 No.of blows, N 11 15 29 32 30 44 0 estigate shear 12%arrow_forwardQ2 A/ State the main field tests which may be carried out to investigate shear strength of a soil layer? B/ What are the main factors that affecting the spacing and number of boreholes for a given project? C/ Illustrate the causes of disturbance of Shelby tubes samples.arrow_forward
- Trolley of the overhead crane moves along the bridge rail. The trolley position is measured from the center of the bridge rail (x = 0) is given by x(t) = 0.5t^3-6t^2+19.5t-14 : 0 <= t <= 3 min. The trolley moves from point A to B in the forward direction, B to C in the reverse direction and C to D again in the forward direction. CONTROL PANEL END TRUCK- RUNWAY BEAM- BRIDGE RAIL HOIST -TROLLEY TROLLEY BUMPER TROLLEY DRIVE LPENDANT TRACK -TROLLEY CONDUCTOR TRACK WIRE ROPE -HOOK BLOCK -BRIDGE DRIVE -END TRUCK BUMPER -RUNWAY RAIL TROLLEY END STOP -CONDUCTOR BAR PENDANT FESTOONING TROLLEY FESTOONING PENDANT CABLE PENDANT x(t)=0.5t^3-6t^2+19.5t-14 v(t)=1.5t^2-12t+19.5 a(t)=(dv(t))/dt=3t-12 Fig. T2.2: The overhead crane Total masses of the trolley, hook block, and the load attached to the hook block are 110 kg, 20 kg, and 150 kg. Damping coefficient, D, is 40 kg/s. What is the total amount of energy required from the trolley motor to move the system [Hint: Use Newton's 2nd law to obtain the…arrow_forwardCONTROL PANEL- BRIDGE RAIL HOIST -TROLLEY TROLLEY BUMPER -BRIDGE DRIVE END TRUCK- RUNWAY BEAM- END TRUCK BUMPER -RUNWAY RAIL TROLLEY DRIVE TROLLEY END STOP -CONDUCTOR BAR LPENDANT TRACK TROLLEY CONDUCTOR TRACK -WIRE ROPE PENDANT FESTOONING TROLLEY FESTOONING -PENDANT CABLE -HOOK BLOCK PENDANTarrow_forwardchool Which of the following functions describes the graph of g(x)--2√9-x²+37 9 8 7 6 4 2 -10-9-8-7-6-5-4-3-2-1 1 -1 -2 -4 -6 10 9 8 B 5 4 3 3 6 -10-9-8-7-6-5-4-3-2-1 2 3 4 6 1 -2 4 -5 -6 -8 -9 -10 10 -10-9-8-7-6-5-4-3-2-1 9 8 Lessons Assessments 6 5 4 + 2 1 1 2 3 4 5 6 8 -1 2 4 -5 -B 8 10 10 9 8 7 6 5 4 3 2 1 -10-9-8-7-6-5-4-3-2-1 1 2 3 4 5 6 B 9 10 -1 -2 -3 -5arrow_forward
- Please sketch questions 1, 2 and 6arrow_forwardsolve questions 3, 4,5, 7, 8, and 9arrow_forward4. Please solve this for me and show every single step. I am studying and got stuck on this practice question, and need help in solving it. Please be very specific and show every step. Thanks. I WANT A HUMAN TO SOLVE THIS PLEASE.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License