Chapter 12.2, Problem 1aT

A cubical block is observed to float in a beaker of water. The block is then held near the center of the beaker as shown and released.

1. Describe the motion of the block after it is released.
2. In the space provided, draw, a free−body diagram for the block at the instant that it is released. Show the forces that the water exerts on each of the surfaces of the block separately.

Make sure the label for each force indicates:

• the type of force,
• the object exerting the force is exerted, and
• the object exerting the force.

Rank the magnitudes of the vertical forces in your free−body diagram. If you cannot completely rank the forces, explain why you cannot.

Did you use the relationship between pressure and depth to compare the magnitudes ofany of the vertical forces? If so, how?

Did you use information about the motion of the block to compare the magnitudes of any of the vertical forces? If so, how?

In the box at right, draw an arrow to represent the vector sum of the forces exerted on the block by the surrounding water. How did you determine the direction?

Is this vector sum the net force on the block? (Recall that the net force is defined as the vector sum of all forces acting on an object.)
Is the magnitude of the sum of the forces exerted on the block by the water greater than, less than, or equal to the weight of the block? Explain.

To determine

To Explain: The motion of the block after it is released in the center of the block.

Explanation of Solution

Introduction:

According to Newton’s second law of motion, anybody under influence of a net force accelerates along the direction of the net force. For an object inside a fluid, the forces along the vertical direction are the upward buoyant force and the downward force of gravity. The object moves along the direction of the dominating force. If the two forces are equal, the object stays at rest.

It is given that the block floats in water, which means when the block is released in the center of the beaker, the upward buoyant force dominates and the block moves in the upward direction. So, after release, the block accelerates towards the surface of the water. After reaching the surface, the block comes to rest at the equilibrium position.

Conclusion:

After releasing, the block accelerates towards the surface of the water.

To determine

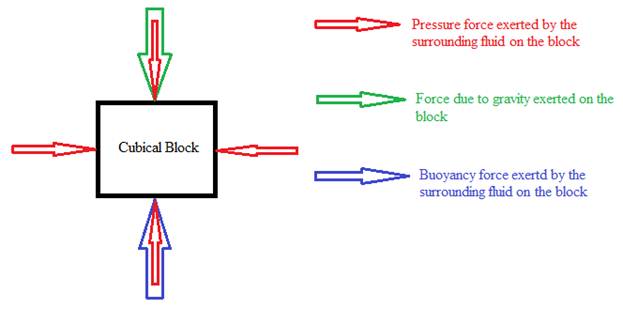
To Draw: A free body diagram of the fully submersed block.

Explanation of Solution

Introduction:

By Archimedes’ principle, the buoyant force (acts upwards) on an object in a fluid is equal to the weight of the water which is displaced by the object. The other forces that act on the object are the downward force due to gravity and the pressure force exerted by the surrounding fluid on the surface of the object. The pressure force exists due to the weight of the water column that lies above the object and acts equally from all directions due to the properties of an incompressible fluid.

The free-body diagram for the block at the instant it is released is given below.

  

To determine

To rank: The magnitudes of the vertical forces in the free body diagram.

If the relationship between pressure and depth is used to compare the magnitudes of vertical forces.

If the information about the motion of the block is used to compare the magnitudes of forces.

Explanation of Solution

Introduction:

If an object is in water, the water above the object exerts pressure on the surface of the object. Due to the properties of the fluid, this pressure is exerted on the object from all directions. The magnitude of this pressure is given by $P=P_o+\rho gh$ . Here, $P_o$ is the atmospheric pressure on the surface of the water, $\rho$ is the density of water, $g$ is the acceleration due to gravity, $h$ is the depth of the object inside water. But because this pressure force acts from all directions, this force cannot initiate any motion in the object.

According to Newton’s second law of motion, anybody under influence of a net force accelerates along the direction of the net force. For an object inside a fluid, the forces along the vertical direction are the upward buoyant force and the downward force of gravity. The object moves along the direction of the dominating force. If the two forces are equal, the object stays at rest.

The different vertical forces that act on the block in the free body diagram are the upward buoyant force ( $F_B$ ), the downward force due to gravity $(F_G)$ and the pressure forces $(F_P)$ that act from all the directions.

Since the block floats on the water, following Newton’s second law, it can be said that the upward buoyant force is larger than the downward force of gravity.

So,

  $F_B>F_G$

But since the pressure force acts equally from all the directions, it does not initiate any motion and cannot be compared with the other forces on the basis of Newton’s second law.

As the block is in a beaker, the depth of the block inside the water is quite negligible. But the atmospheric pressure term is very large as compared to any other vertical force $\left({10}^5\text{ N/m}\right)$ . So the comparison must be as follows,

  $F_P>F_B>F_G$

Conclusion:

  $F_P>F_B>F_G$

The relationship between pressure and depth is used.

The information about the motion of the block is used.

To determine

To draw: The vector sum of all the forces on the block and explain it.

Explanation of Solution

Introduction:

According to Newton’s second law of motion, anybody under influence of a net force accelerates along the direction of the net force. For an object in a fluid, the forces along the vertical direction are the upward buoyant force and the downward force of gravity. The object moves along the direction of the dominating force. If the two forces are equal, the object stays at rest. One other force that acts on the object is the pressure force due to the weight of the water column above the object. But this force acts equally from all directions. So, the resultant of this force on the object is zero.

The arrow in the box below represents the vector sum of all the forces exerted by the surrounding water on the block.

  

The direction of this force can be determined by the fact that the vector sum of the pressure forces exerted by the surrounding water is zero. So, the only force exerted by the surrounding water that remains is the upward buoyant force.

This force is not the vector sum of the net forces on the block. Because this force is only the vector sum of the forces exerted by the fluid on the block. The one other force that acts on the block is the force due to gravity (weight of the block). The vector sum of these two forces is the net force on the block.

As the block tends to move in the upward direction after release, the net force on the block must be in the upward direction. i.e. the magnitude of all the forces exerted on the block by the water is greater than the weight of the block.

Conclusion:

The net force exerted by the water on the block is in the upward direction.

This force is not equal to the vector sum of all the forces on the block.

The buoyant force on the block is greater than the weight of the block.