Introductory and Intermediate Algebra for College Students (5th Edition)
5th Edition
ISBN: 9780134178141
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 12.1, Problem 62ES
Use a calculator with an ex key to solve Exercises 57—63. The bar graph shows the percentage of U.S. high school seniors who applied to more than three colleges for selected years from 1980 through 2013.
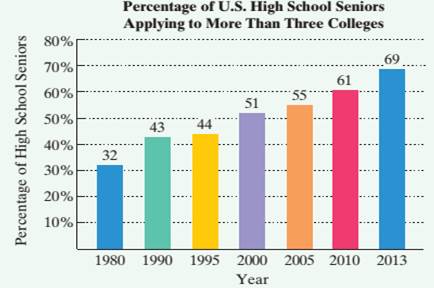
Source: The Higher Education Research Institute
The data in the bar graph at the bottom of the previous page can he modeled by
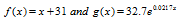
in which f(x) and g(x) represent the percentage of high school seniors who applied to more than three colleges x years after 1980. Use these functions to solve Exercises 57—58. Where necessary, round answers to the nearest percent.
57. a. According to the linear model, what percentage of high school seniors applied to more than three colleges in 2013?
b. According to the exponential model, what percentage of high school seniors applied to more than three colleges in 2013?
c. Which function is a better model for the data shown by the bar graph in 2013?
58. a. According to the linear model, what percentage of high school seniors applied to more than three colleges in 2010?
b. According to the exponential model, what percentage of high school seniors applied to more than three colleges in 2010?
c. Which function is a better model for the data shown by the bar graph in 2010?
59. In college, we study large volumes of information- information that, unfortunately, we do not often retain for very long. The function
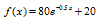
describes the percentage of information, f(x), that a particular person remembers x weeks after learning the information.
a. Substitute 0 for x and, without using a calculator, find the percentage of information remembered at the moment it is first learned.
b. Substitute 1 for x and find the percentage of information that is remembered after 1 week.
c. Find the percentage of information that is remembered after 4 weeks.
d. Find the percentage of information that is remembered after one year (52 weeks).
60. In 1626. Peter Minuit persuaded the Wappinger Indians to sell him Manhattan Island for $24. If the Native Americans had put the $24 into a bank account paying 5% interest, how much would the investment have been worth in the year 2005 if interest were compounded
a. monthly?
b. continuously?
The function
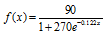
models the percentage, f(x), of people x years old with some
coronary heart disease. Use this function to solve Exercises 61-62. Round answers to the nearest tenth of a percent.
61. Evaluate f(30) and describe what this means in practical terms
62. Evaluate f(70) and describe what this means in practical terms.
63. The function
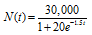
describes the number of people, N(t), who become ill with influenza t weeks after its initial outbreak in a town with 30,000 inhabitants. The horizontal asymptote in the graph indicates that there is a limit to the epidemic's growth.
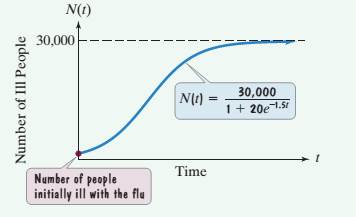
a. How many people became ill with the flu when the epidemic began? (When the epidemic began, t = 0.)
b. How many people were ill by the end of the third week?
c. Why can't the spread of an epidemic simply grow indefinitely? What does the horizontal asymptote shown in the graph indicate about the limiting size of the population that becomes ill?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Name
Assume there is the following simplified grade book:
Homework Labs | Final Exam | Project
Avery
95
98
90
100
Blake
90
96
Carlos
83
79
Dax
55
30
228
92
95
79
90
65
60
Assume that the weights used to compute the final grades are homework 0.3, labs 0.2,
the final 0.35, and the project 0.15.
| Write an explicit formula to compute Avery's final grade using a single
inner product.
Write an explicit formula to compute everyone's final grade simultane-
ously using a single matrix-vector product.
1. Explicitly compute by hand (with work shown) the following Frobenius inner
products
00
4.56 3.12
(a) ((º º º). (156
(b)
10.9
-1
0
2)),
Fro
5')) Fro
3.
Let
4 0
0
00 0
0
1.2
0
00 0
0
0
-10.1 0 0
0
D =
0
0
0
00 0
0
0
0
05 0
0
0
0
0 0 2.8
Either explicitly compute D-¹ or explain why it doesn't exist.
Chapter 12 Solutions
Introductory and Intermediate Algebra for College Students (5th Edition)
Ch. 12.1 - Fill in each blank SO that the resulting statement...Ch. 12.1 - Prob. 2CAVCCh. 12.1 - Prob. 3CAVCCh. 12.1 - Prob. 4CAVCCh. 12.1 - Prob. 5CAVCCh. 12.1 - Prob. 1ESCh. 12.1 - Prob. 2ESCh. 12.1 - Prob. 3ESCh. 12.1 - Prob. 4ESCh. 12.1 - Prob. 5ES
Ch. 12.1 - Prob. 6ESCh. 12.1 - Prob. 7ESCh. 12.1 - Prob. 8ESCh. 12.1 - Prob. 9ESCh. 12.1 - Prob. 10ESCh. 12.1 - Prob. 11ESCh. 12.1 - In Exercises 11—16, set up a table of coordinates...Ch. 12.1 - Prob. 13ESCh. 12.1 - Prob. 14ESCh. 12.1 - Prob. 15ESCh. 12.1 - In Exercises 11—16, set up a table of coordinates...Ch. 12.1 - Prob. 17ESCh. 12.1 - Prob. 18ESCh. 12.1 - Prob. 19ESCh. 12.1 - Prob. 20ESCh. 12.1 - Prob. 21ESCh. 12.1 - Prob. 22ESCh. 12.1 - Prob. 23ESCh. 12.1 - Prob. 24ESCh. 12.1 - Prob. 25ESCh. 12.1 - Prob. 26ESCh. 12.1 - Prob. 27ESCh. 12.1 - Prob. 28ESCh. 12.1 - Prob. 29ESCh. 12.1 - Prob. 30ESCh. 12.1 - Prob. 31ESCh. 12.1 - Prob. 32ESCh. 12.1 - Prob. 33ESCh. 12.1 - Prob. 34ESCh. 12.1 - Prob. 35ESCh. 12.1 - Prob. 36ESCh. 12.1 - Prob. 37ESCh. 12.1 - Prob. 38ESCh. 12.1 - Use the compound interest formulas, and , to solve...Ch. 12.1 - Prob. 40ESCh. 12.1 - Use the compound interest formulas, and , to solve...Ch. 12.1 - Use the compound interest formulas, and , to solve...Ch. 12.1 - Prob. 43ESCh. 12.1 - Prob. 44ESCh. 12.1 - Prob. 45ESCh. 12.1 - Prob. 46ESCh. 12.1 - Prob. 47ESCh. 12.1 - Prob. 48ESCh. 12.1 - In Exercises 49—50, graph f and g in the same...Ch. 12.1 - In Exercises 49—50, graph f and g in the same...Ch. 12.1 - Prob. 51ESCh. 12.1 - Prob. 52ESCh. 12.1 - Prob. 53ESCh. 12.1 - Use a calculator with a yx key or a ^ key to solve...Ch. 12.1 - Prob. 55ESCh. 12.1 - Prob. 56ESCh. 12.1 - Prob. 57ESCh. 12.1 - Prob. 58ESCh. 12.1 - Prob. 59ESCh. 12.1 - Use a calculator with an ex key to solve Exercises...Ch. 12.1 - Prob. 61ESCh. 12.1 - Use a calculator with an ex key to solve Exercises...Ch. 12.1 - Use a calculator with an ex key to solve Exercises...Ch. 12.1 - Prob. 64ESCh. 12.1 - Prob. 65ESCh. 12.1 - Prob. 66ESCh. 12.1 - Prob. 67ESCh. 12.1 - Prob. 68ESCh. 12.1 - Prob. 69ESCh. 12.1 - Prob. 70ESCh. 12.1 - Prob. 71ESCh. 12.1 - Prob. 72ESCh. 12.1 - Prob. 73ESCh. 12.1 - Prob. 74ESCh. 12.1 - Prob. 75ESCh. 12.1 - Prob. 76ESCh. 12.1 - Prob. 77ESCh. 12.1 - Prob. 78ESCh. 12.1 - Prob. 79ESCh. 12.1 - The hyperbolic cosine and hyperbolic sine...Ch. 12.1 - Prob. 81ESCh. 12.1 - Prob. 82ESCh. 12.1 - Prob. 83ESCh. 12.1 - Prob. 84ESCh. 12.1 - Prob. 85ESCh. 12.1 - Prob. 86ESCh. 12.2 - Prob. 1CAVCCh. 12.2 - Prob. 2CAVCCh. 12.2 - Prob. 3CAVCCh. 12.2 - Prob. 4CAVCCh. 12.2 - Prob. 5CAVCCh. 12.2 - Prob. 6CAVCCh. 12.2 - Prob. 7CAVCCh. 12.2 - Prob. 8CAVCCh. 12.2 - Prob. 9CAVCCh. 12.2 - Prob. 10CAVCCh. 12.2 - Prob. 11CAVCCh. 12.2 - Prob. 1ESCh. 12.2 - Prob. 2ESCh. 12.2 - Prob. 3ESCh. 12.2 - Prob. 4ESCh. 12.2 - Prob. 5ESCh. 12.2 - Prob. 6ESCh. 12.2 - Prob. 7ESCh. 12.2 - Prob. 8ESCh. 12.2 - Prob. 9ESCh. 12.2 - Prob. 10ESCh. 12.2 - Prob. 11ESCh. 12.2 - Prob. 12ESCh. 12.2 - Prob. 13ESCh. 12.2 - Prob. 14ESCh. 12.2 - Prob. 15ESCh. 12.2 - Prob. 16ESCh. 12.2 - Prob. 17ESCh. 12.2 - Prob. 18ESCh. 12.2 - Prob. 19ESCh. 12.2 - Prob. 20ESCh. 12.2 - Prob. 21ESCh. 12.2 - Prob. 22ESCh. 12.2 - Prob. 23ESCh. 12.2 - Prob. 24ESCh. 12.2 - Prob. 25ESCh. 12.2 - Prob. 26ESCh. 12.2 - Prob. 27ESCh. 12.2 - Prob. 28ESCh. 12.2 - Prob. 29ESCh. 12.2 - Prob. 30ESCh. 12.2 - Prob. 31ESCh. 12.2 - Prob. 32ESCh. 12.2 - Prob. 33ESCh. 12.2 - Prob. 34ESCh. 12.2 - Prob. 35ESCh. 12.2 - Prob. 36ESCh. 12.2 - Prob. 37ESCh. 12.2 - Prob. 38ESCh. 12.2 - Prob. 39ESCh. 12.2 - Prob. 40ESCh. 12.2 - Prob. 41ESCh. 12.2 - Prob. 42ESCh. 12.2 - Prob. 43ESCh. 12.2 - Prob. 44ESCh. 12.2 - Prob. 45ESCh. 12.2 - Prob. 46ESCh. 12.2 - Prob. 47ESCh. 12.2 - Prob. 48ESCh. 12.2 - Prob. 49ESCh. 12.2 - Prob. 50ESCh. 12.2 - Prob. 51ESCh. 12.2 - Prob. 52ESCh. 12.2 - Prob. 53ESCh. 12.2 - Prob. 54ESCh. 12.2 - Prob. 55ESCh. 12.2 - Prob. 56ESCh. 12.2 - Prob. 57ESCh. 12.2 - Prob. 58ESCh. 12.2 - Prob. 59ESCh. 12.2 - Prob. 60ESCh. 12.2 - Prob. 61ESCh. 12.2 - Prob. 62ESCh. 12.2 - Prob. 63ESCh. 12.2 - Prob. 64ESCh. 12.2 - Prob. 65ESCh. 12.2 - Prob. 66ESCh. 12.2 - Prob. 67ESCh. 12.2 - Prob. 68ESCh. 12.2 - Prob. 69ESCh. 12.2 - Prob. 70ESCh. 12.2 - Prob. 71ESCh. 12.2 - Prob. 72ESCh. 12.2 - Prob. 73ESCh. 12.2 - Prob. 74ESCh. 12.2 - Prob. 75ESCh. 12.2 - Prob. 76ESCh. 12.2 - Prob. 77ESCh. 12.2 - Prob. 78ESCh. 12.2 - Prob. 79ESCh. 12.2 - Prob. 80ESCh. 12.2 - Prob. 81ESCh. 12.2 - Prob. 82ESCh. 12.2 - Prob. 83ESCh. 12.2 - Prob. 84ESCh. 12.2 - Prob. 85ESCh. 12.2 - Prob. 86ESCh. 12.2 - Prob. 87ESCh. 12.2 - Prob. 88ESCh. 12.2 - Prob. 89ESCh. 12.2 - Prob. 90ESCh. 12.2 - Prob. 91ESCh. 12.2 - Prob. 92ESCh. 12.2 - Prob. 93ESCh. 12.2 - Prob. 94ESCh. 12.2 - Prob. 95ESCh. 12.2 - Prob. 96ESCh. 12.2 - Prob. 97ESCh. 12.2 - Prob. 98ESCh. 12.2 - Prob. 99ESCh. 12.2 - Prob. 100ESCh. 12.2 - Prob. 101ESCh. 12.2 - Prob. 102ESCh. 12.2 - Prob. 103ESCh. 12.2 - Prob. 104ESCh. 12.2 - Prob. 105ESCh. 12.2 - Prob. 106ESCh. 12.2 - Prob. 107ESCh. 12.2 - Prob. 108ESCh. 12.2 - Prob. 109ESCh. 12.2 - Prob. 110ESCh. 12.2 - Prob. 111ESCh. 12.2 - Prob. 112ESCh. 12.2 - In Exercises 113–116, determine whether each...Ch. 12.2 - Prob. 114ESCh. 12.2 - Prob. 115ESCh. 12.2 - Prob. 116ESCh. 12.2 - Prob. 117ESCh. 12.2 - Prob. 118ESCh. 12.2 - Prob. 119ESCh. 12.2 - Prob. 120ESCh. 12.2 - Prob. 121ESCh. 12.2 - Prob. 122ESCh. 12.2 - Prob. 123ESCh. 12.2 - Prob. 124ESCh. 12.2 - Prob. 125ESCh. 12.3 - Prob. 1CAVCCh. 12.3 - Prob. 2CAVCCh. 12.3 - Prob. 3CAVCCh. 12.3 - Prob. 4CAVCCh. 12.3 - Prob. 1ESCh. 12.3 - Prob. 2ESCh. 12.3 - Prob. 3ESCh. 12.3 - Prob. 4ESCh. 12.3 - Prob. 5ESCh. 12.3 - Prob. 6ESCh. 12.3 - Prob. 7ESCh. 12.3 - Prob. 8ESCh. 12.3 - Prob. 9ESCh. 12.3 - Prob. 10ESCh. 12.3 - Prob. 11ESCh. 12.3 - Prob. 12ESCh. 12.3 - Prob. 13ESCh. 12.3 - Prob. 14ESCh. 12.3 - Prob. 15ESCh. 12.3 - Prob. 16ESCh. 12.3 - Prob. 17ESCh. 12.3 - Prob. 18ESCh. 12.3 - Prob. 19ESCh. 12.3 - Prob. 20ESCh. 12.3 - Prob. 21ESCh. 12.3 - Prob. 22ESCh. 12.3 - Prob. 23ESCh. 12.3 - Prob. 24ESCh. 12.3 - Prob. 25ESCh. 12.3 - Prob. 26ESCh. 12.3 - Prob. 27ESCh. 12.3 - Prob. 28ESCh. 12.3 - Prob. 29ESCh. 12.3 - Prob. 30ESCh. 12.3 - Prob. 31ESCh. 12.3 - Prob. 32ESCh. 12.3 - Prob. 33ESCh. 12.3 - Prob. 34ESCh. 12.3 - Prob. 35ESCh. 12.3 - Prob. 36ESCh. 12.3 - Prob. 37ESCh. 12.3 - Prob. 38ESCh. 12.3 - Prob. 39ESCh. 12.3 - Prob. 40ESCh. 12.3 - Prob. 41ESCh. 12.3 - Prob. 42ESCh. 12.3 - Prob. 43ESCh. 12.3 - Prob. 44ESCh. 12.3 - Prob. 45ESCh. 12.3 - Prob. 46ESCh. 12.3 - Prob. 47ESCh. 12.3 - Prob. 48ESCh. 12.3 - Prob. 49ESCh. 12.3 - Prob. 50ESCh. 12.3 - Prob. 51ESCh. 12.3 - Prob. 52ESCh. 12.3 - Prob. 53ESCh. 12.3 - Prob. 54ESCh. 12.3 - Prob. 55ESCh. 12.3 - Prob. 56ESCh. 12.3 - Prob. 57ESCh. 12.3 - Prob. 58ESCh. 12.3 - Prob. 59ESCh. 12.3 - Prob. 60ESCh. 12.3 - Prob. 61ESCh. 12.3 - Prob. 62ESCh. 12.3 - Prob. 63ESCh. 12.3 - Prob. 64ESCh. 12.3 - Prob. 65ESCh. 12.3 - Prob. 66ESCh. 12.3 - Prob. 67ESCh. 12.3 - Prob. 68ESCh. 12.3 - Prob. 69ESCh. 12.3 - Prob. 70ESCh. 12.3 - Prob. 71ESCh. 12.3 - Prob. 72ESCh. 12.3 - Prob. 73ESCh. 12.3 - Prob. 74ESCh. 12.3 - Prob. 75ESCh. 12.3 - Prob. 76ESCh. 12.3 - Prob. 77ESCh. 12.3 - Prob. 78ESCh. 12.3 - Prob. 79ESCh. 12.3 - Prob. 80ESCh. 12.3 - Prob. 81ESCh. 12.3 - Prob. 82ESCh. 12.3 - Prob. 83ESCh. 12.3 - Prob. 84ESCh. 12.3 - Prob. 85ESCh. 12.3 - Prob. 86ESCh. 12.3 - Prob. 87ESCh. 12.3 - Prob. 88ESCh. 12.3 - Prob. 89ESCh. 12.3 - Prob. 90ESCh. 12.3 - Prob. 91ESCh. 12.3 - Prob. 92ESCh. 12.3 - Prob. 93ESCh. 12.3 - Prob. 94ESCh. 12.3 - Prob. 95ESCh. 12.3 - Prob. 96ESCh. 12.3 - Prob. 97ESCh. 12.3 - Prob. 98ESCh. 12.3 - Prob. 99ESCh. 12.3 - Prob. 100ESCh. 12.3 - Prob. 101ESCh. 12.3 - Prob. 102ESCh. 12.3 - a. Use a graphing utility (and the change-of-base...Ch. 12.3 - Prob. 104ESCh. 12.3 - Prob. 105ESCh. 12.3 - Prob. 106ESCh. 12.3 - Disprove each statement in Exercises 106–110...Ch. 12.3 - Prob. 108ESCh. 12.3 - Prob. 109ESCh. 12.3 - Prob. 110ESCh. 12.3 - Prob. 111ESCh. 12.3 - Prob. 112ESCh. 12.3 - Prob. 113ESCh. 12.3 - Prob. 114ESCh. 12.3 - Prob. 115ESCh. 12.3 - Prob. 116ESCh. 12.3 - Prob. 117ESCh. 12.3 - Prob. 118ESCh. 12.3 - Prob. 119ESCh. 12.3 - Prob. 120ESCh. 12.3 - Prob. 121ESCh. 12.3 - Prob. 122ESCh. 12.3 - Prob. 123ESCh. 12.3 - Prob. 124ESCh. 12.3 - Prob. 125ESCh. 12.3 - Prob. 126ESCh. 12.3 - Prob. 127ESCh. 12.4 - Fill in each blank so that the resulting statement...Ch. 12.4 - Prob. 2CAVCCh. 12.4 - Prob. 3CAVCCh. 12.4 - Prob. 4CAVCCh. 12.4 - Prob. 5CAVCCh. 12.4 - Prob. 6CAVCCh. 12.4 - Prob. 7CAVCCh. 12.4 - Prob. 8CAVCCh. 12.4 - Prob. 9CAVCCh. 12.4 - Prob. 10CAVCCh. 12.4 - Prob. 1ESCh. 12.4 - Prob. 2ESCh. 12.4 - Prob. 3ESCh. 12.4 - Prob. 4ESCh. 12.4 - Prob. 5ESCh. 12.4 - Prob. 6ESCh. 12.4 - Prob. 7ESCh. 12.4 - Prob. 8ESCh. 12.4 - Prob. 9ESCh. 12.4 - Prob. 10ESCh. 12.4 - Prob. 11ESCh. 12.4 - Prob. 12ESCh. 12.4 - Prob. 13ESCh. 12.4 - Prob. 14ESCh. 12.4 - Prob. 15ESCh. 12.4 - Prob. 16ESCh. 12.4 - Prob. 17ESCh. 12.4 - Prob. 18ESCh. 12.4 - Prob. 19ESCh. 12.4 - Prob. 20ESCh. 12.4 - Prob. 21ESCh. 12.4 - Prob. 22ESCh. 12.4 - Prob. 23ESCh. 12.4 - Prob. 24ESCh. 12.4 - Prob. 25ESCh. 12.4 - Prob. 26ESCh. 12.4 - Prob. 27ESCh. 12.4 - Prob. 28ESCh. 12.4 - Prob. 29ESCh. 12.4 - Prob. 30ESCh. 12.4 - Prob. 31ESCh. 12.4 - Prob. 32ESCh. 12.4 - Solve each exponential equation in Exercises 1940...Ch. 12.4 - Prob. 34ESCh. 12.4 - Prob. 35ESCh. 12.4 - Prob. 36ESCh. 12.4 - Prob. 37ESCh. 12.4 - Prob. 38ESCh. 12.4 - Prob. 39ESCh. 12.4 - Prob. 40ESCh. 12.4 - Prob. 41ESCh. 12.4 - Prob. 42ESCh. 12.4 - Prob. 43ESCh. 12.4 - Prob. 44ESCh. 12.4 - Prob. 45ESCh. 12.4 - Prob. 46ESCh. 12.4 - Prob. 47ESCh. 12.4 - Prob. 48ESCh. 12.4 - Prob. 49ESCh. 12.4 - Prob. 50ESCh. 12.4 - Prob. 51ESCh. 12.4 - Prob. 52ESCh. 12.4 - Prob. 53ESCh. 12.4 - Prob. 54ESCh. 12.4 - Prob. 55ESCh. 12.4 - Prob. 56ESCh. 12.4 - Prob. 57ESCh. 12.4 - Prob. 58ESCh. 12.4 - Prob. 59ESCh. 12.4 - Prob. 60ESCh. 12.4 - Prob. 61ESCh. 12.4 - Prob. 62ESCh. 12.4 - Prob. 63ESCh. 12.4 - Prob. 64ESCh. 12.4 - Prob. 65ESCh. 12.4 - Prob. 66ESCh. 12.4 - Prob. 67ESCh. 12.4 - Prob. 68ESCh. 12.4 - Prob. 69ESCh. 12.4 - Prob. 70ESCh. 12.4 - Prob. 71ESCh. 12.4 - Prob. 72ESCh. 12.4 - Prob. 73ESCh. 12.4 - Prob. 74ESCh. 12.4 - Prob. 75ESCh. 12.4 - Prob. 76ESCh. 12.4 - Prob. 77ESCh. 12.4 - Prob. 78ESCh. 12.4 - Prob. 79ESCh. 12.4 - Prob. 80ESCh. 12.4 - Prob. 81ESCh. 12.4 - Prob. 82ESCh. 12.4 - Prob. 83ESCh. 12.4 - Prob. 84ESCh. 12.4 - Prob. 85ESCh. 12.4 - Prob. 86ESCh. 12.4 - Prob. 87ESCh. 12.4 - Prob. 88ESCh. 12.4 - Prob. 89ESCh. 12.4 - Prob. 90ESCh. 12.4 - Prob. 91ESCh. 12.4 - Prob. 92ESCh. 12.4 - Prob. 93ESCh. 12.4 - Prob. 94ESCh. 12.4 - Prob. 95ESCh. 12.4 - Prob. 96ESCh. 12.4 - Prob. 97ESCh. 12.4 - Prob. 98ESCh. 12.4 - Prob. 99ESCh. 12.4 - Prob. 100ESCh. 12.4 - Prob. 101ESCh. 12.4 - Prob. 102ESCh. 12.4 - Prob. 103ESCh. 12.4 - Prob. 104ESCh. 12.4 - Prob. 105ESCh. 12.4 - Prob. 106ESCh. 12.4 - Prob. 107ESCh. 12.4 - Prob. 108ESCh. 12.4 - Prob. 109ESCh. 12.4 - Prob. 110ESCh. 12.4 - Prob. 111ESCh. 12.4 - Prob. 112ESCh. 12.4 - Prob. 113ESCh. 12.4 - The function P(x) = 95 - 30 log2x models the...Ch. 12.4 - Prob. 115ESCh. 12.4 - Prob. 116ESCh. 12.4 - Prob. 117ESCh. 12.4 - Prob. 118ESCh. 12.4 - Prob. 119ESCh. 12.4 - Prob. 120ESCh. 12.4 - Prob. 121ESCh. 12.4 - Prob. 122ESCh. 12.4 - Prob. 123ESCh. 12.4 - Prob. 124ESCh. 12.4 - Prob. 125ESCh. 12.4 - Prob. 126ESCh. 12.4 - Prob. 127ESCh. 12.4 - Prob. 128ESCh. 12.4 - Prob. 129ESCh. 12.4 - Prob. 130ESCh. 12.4 - Prob. 131ESCh. 12.4 - Prob. 132ESCh. 12.4 - Prob. 133ESCh. 12.4 - Prob. 134ESCh. 12.4 - Prob. 135ESCh. 12.4 - Prob. 136ESCh. 12.4 - Prob. 137ESCh. 12.4 - Prob. 138ESCh. 12.4 - Prob. 139ESCh. 12.4 - Prob. 140ESCh. 12.4 - Prob. 141ESCh. 12.4 - Prob. 142ESCh. 12.4 - Prob. 143ESCh. 12.4 - Prob. 144ESCh. 12.4 - Prob. 145ESCh. 12.4 - Prob. 146ESCh. 12.4 - Prob. 147ESCh. 12.4 - Prob. 148ESCh. 12.4 - Prob. 149ESCh. 12.4 - Prob. 150ESCh. 12.4 - Prob. 151ESCh. 12.4 - Prob. 152ESCh. 12.5 - Prob. 1CAVCCh. 12.5 - Prob. 2CAVCCh. 12.5 - Prob. 3CAVCCh. 12.5 - Prob. 4CAVCCh. 12.5 - Prob. 5CAVCCh. 12.5 - Prob. 6CAVCCh. 12.5 - The exponential models describe the population of...Ch. 12.5 - Prob. 2ESCh. 12.5 - Prob. 3ESCh. 12.5 - Prob. 4ESCh. 12.5 - Prob. 5ESCh. 12.5 - The exponential models describe the population of...Ch. 12.5 - Prob. 7ESCh. 12.5 - Prob. 8ESCh. 12.5 - In Exercises 9-14, complete the table. Round...Ch. 12.5 - Prob. 10ESCh. 12.5 - Prob. 11ESCh. 12.5 - Prob. 12ESCh. 12.5 - Prob. 13ESCh. 12.5 - Prob. 14ESCh. 12.5 - Prob. 15ESCh. 12.5 - Prob. 16ESCh. 12.5 - The half-life of the radioactive element...Ch. 12.5 - Prob. 18ESCh. 12.5 - Prob. 19ESCh. 12.5 - Prob. 20ESCh. 12.5 - Prob. 21ESCh. 12.5 - Prob. 22ESCh. 12.5 - Prob. 23ESCh. 12.5 - Prob. 24ESCh. 12.5 - Prob. 25ESCh. 12.5 - In Exercise 21-26, complete the table. Round...Ch. 12.5 - Prob. 27ESCh. 12.5 - Prob. 28ESCh. 12.5 - Prob. 29ESCh. 12.5 - Prob. 30ESCh. 12.5 - Prob. 31ESCh. 12.5 - Prob. 32ESCh. 12.5 - Prob. 33ESCh. 12.5 - Prob. 34ESCh. 12.5 - Prob. 35ESCh. 12.5 - Prob. 36ESCh. 12.5 - Prob. 37ESCh. 12.5 - Prob. 38ESCh. 12.5 - Prob. 39ESCh. 12.5 - Prob. 40ESCh. 12.5 - Prob. 41ESCh. 12.5 - Prob. 42ESCh. 12.5 - Prob. 43ESCh. 12.5 - Prob. 44ESCh. 12.5 - Prob. 45ESCh. 12.5 - Prob. 46ESCh. 12.5 - Prob. 47ESCh. 12.5 - How can you tell if an exponential model describes...Ch. 12.5 - Prob. 49ESCh. 12.5 - Prob. 50ESCh. 12.5 - Prob. 51ESCh. 12.5 - Prob. 52ESCh. 12.5 - Prob. 53ESCh. 12.5 - Prob. 54ESCh. 12.5 - In Example 1 on page 912, we used two data points...Ch. 12.5 - Prob. 56ESCh. 12.5 - In Example 1 on page 912, we used two data points...Ch. 12.5 - Prob. 58ESCh. 12.5 - Prob. 59ESCh. 12.5 - Prob. 60ESCh. 12.5 - Prob. 61ESCh. 12.5 - Prob. 62ESCh. 12.5 - Prob. 63ESCh. 12.5 - Prob. 64ESCh. 12.5 - Prob. 65ESCh. 12.5 - Prob. 66ESCh. 12.5 - Prob. 67ESCh. 12.5 - Prob. 68ESCh. 12.5 - Prob. 69ESCh. 12.5 - Prob. 70ESCh. 12.5 - Prob. 71ESCh. 12.5 - Prob. 72ESCh. 12.5 - Prob. 73ESCh. 12.5 - Prob. 74ESCh. 12.5 - Prob. 75ESCh. 12.5 - Prob. 76ESCh. 12 - Prob. 1MCPCh. 12 - Prob. 2MCPCh. 12 - Prob. 3MCPCh. 12 - Prob. 4MCPCh. 12 - Prob. 5MCPCh. 12 - Prob. 6MCPCh. 12 - Prob. 7MCPCh. 12 - Prob. 8MCPCh. 12 - Prob. 9MCPCh. 12 - Prob. 10MCPCh. 12 - Prob. 11MCPCh. 12 - Prob. 12MCPCh. 12 - Prob. 13MCPCh. 12 - Prob. 14MCPCh. 12 - Prob. 15MCPCh. 12 - Prob. 16MCPCh. 12 - Prob. 17MCPCh. 12 - Prob. 18MCPCh. 12 - Prob. 19MCPCh. 12 - Prob. 20MCPCh. 12 - Prob. 21MCPCh. 12 - Prob. 22MCPCh. 12 - Prob. 23MCPCh. 12 - Prob. 24MCPCh. 12 - Prob. 25MCPCh. 12 - Prob. 1RECh. 12 - Prob. 2RECh. 12 - Prob. 3RECh. 12 - Prob. 4RECh. 12 - Prob. 5RECh. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Prob. 15RECh. 12 - Prob. 16RECh. 12 - Prob. 17RECh. 12 - Prob. 18RECh. 12 - Prob. 19RECh. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RECh. 12 - Prob. 27RECh. 12 - Prob. 28RECh. 12 - Prob. 29RECh. 12 - Prob. 30RECh. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Prob. 34RECh. 12 - Prob. 35RECh. 12 - Prob. 36RECh. 12 - Prob. 37RECh. 12 - Prob. 38RECh. 12 - Prob. 39RECh. 12 - Prob. 40RECh. 12 - Prob. 41RECh. 12 - Prob. 42RECh. 12 - Prob. 43RECh. 12 - Prob. 44RECh. 12 - Prob. 45RECh. 12 - Prob. 46RECh. 12 - Prob. 47RECh. 12 - Prob. 48RECh. 12 - Prob. 49RECh. 12 - Prob. 50RECh. 12 - Prob. 51RECh. 12 - Prob. 52RECh. 12 - Prob. 53RECh. 12 - Prob. 54RECh. 12 - Prob. 55RECh. 12 - Prob. 56RECh. 12 - Prob. 57RECh. 12 - Prob. 58RECh. 12 - Prob. 59RECh. 12 - Prob. 60RECh. 12 - Prob. 61RECh. 12 - Prob. 62RECh. 12 - Prob. 63RECh. 12 - Prob. 64RECh. 12 - Prob. 65RECh. 12 - Prob. 66RECh. 12 - Prob. 67RECh. 12 - Prob. 68RECh. 12 - Prob. 69RECh. 12 - Prob. 70RECh. 12 - Prob. 71RECh. 12 - Prob. 72RECh. 12 - Prob. 73RECh. 12 - Prob. 74RECh. 12 - Prob. 75RECh. 12 - Prob. 76RECh. 12 - Prob. 77RECh. 12 - Prob. 78RECh. 12 - Prob. 79RECh. 12 - Prob. 80RECh. 12 - Prob. 81RECh. 12 - Prob. 82RECh. 12 - Prob. 83RECh. 12 - Prob. 1TCh. 12 - Prob. 2TCh. 12 - Prob. 3TCh. 12 - Prob. 4TCh. 12 - Prob. 5TCh. 12 - Prob. 6TCh. 12 - Prob. 7TCh. 12 - Prob. 8TCh. 12 - Prob. 9TCh. 12 - Prob. 10TCh. 12 - Prob. 11TCh. 12 - Prob. 12TCh. 12 - Prob. 13TCh. 12 - Prob. 14TCh. 12 - Prob. 15TCh. 12 - Prob. 16TCh. 12 - Prob. 17TCh. 12 - Prob. 18TCh. 12 - Prob. 19TCh. 12 - Prob. 20TCh. 12 - Prob. 21TCh. 12 - Prob. 22TCh. 12 - Prob. 23TCh. 12 - Prob. 24TCh. 12 - Prob. 25TCh. 12 - Prob. 26TCh. 12 - Prob. 27TCh. 12 - Prob. 28TCh. 12 - Prob. 29TCh. 12 - Prob. 30TCh. 12 - Prob. 31TCh. 12 - Prob. 32TCh. 12 - Prob. 33TCh. 12 - Prob. 1CRECh. 12 - Prob. 2CRECh. 12 - Prob. 3CRECh. 12 - Prob. 4CRECh. 12 - Prob. 5CRECh. 12 - Prob. 6CRECh. 12 - Prob. 7CRECh. 12 - Prob. 8CRECh. 12 - Prob. 9CRECh. 12 - Prob. 10CRECh. 12 - Prob. 11CRECh. 12 - Prob. 12CRECh. 12 - Prob. 13CRECh. 12 - Prob. 14CRECh. 12 - Prob. 15CRECh. 12 - Prob. 16CRECh. 12 - Prob. 17CRECh. 12 - Prob. 18CRECh. 12 - Prob. 19CRECh. 12 - Prob. 20CRECh. 12 - Prob. 21CRECh. 12 - In Exercises 2125, perform the indicated...Ch. 12 - Prob. 23CRECh. 12 - Prob. 24CRECh. 12 - Prob. 25CRECh. 12 - Prob. 26CRECh. 12 - Prob. 27CRECh. 12 - Prob. 28CRECh. 12 - Prob. 29CRECh. 12 - Prob. 30CRECh. 12 - Prob. 31CRECh. 12 - Prob. 32CRE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- 4. [9 points] Assume that B, C, E are all 3 x 3 matrices such that BC == -64 -1 0 3 4 4 4 -2 2 CB=-1-2 4 BE -2 1 3 EC = 1 3 2 -7, 1 6 -6 2-5 -7 -2 Explicitly compute the following by hand. (I.e., write out the entries of the 3 × 3 matrix.) (a) [3 points] B(E+C) (b) [3 points] (E+B)C (c) [3 points] ETBTarrow_forward6. Consider the matrices G = 0 (3) -3\ -3 2 and H = -1 2 0 5 0 5 5 noting that H(:, 3) = 2H(:,1) + H(:, 2). Is G invertible? Explain your answer. Is H invertible? Explain your answer. Use co-factor expansion to find the determinant of H. (Hint: expand the 2nd or 3rd row)arrow_forwardFor the matrix A = = ( 6 }) . explicitly compute by hand (with work shown) the following. I2A, where I2 is the 2 × 2 identity matrix. A-1 solving the following linear systems by using A-¹: c+y= 1 y = 1 (d) (e) (f) A² find the diagonal entries of Aarrow_forward
- If 3x−y=12, what is the value of 8x / 2y A) 212B) 44C) 82D) The value cannot be determined from the information given.arrow_forwardC=59(F−32) The equation above shows how temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true? A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit. A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius. A) I onlyB) II onlyC) III onlyD) I and II onlyarrow_forward(1) Let F be a field, show that the vector space F,NEZ* be a finite dimension. (2) Let P2(x) be the vector space of polynomial of degree equal or less than two and M={a+bx+cx²/a,b,cЄ R,a+b=c),show that whether Mis hyperspace or not. (3) Let A and B be a subset of a vector space such that ACB, show that whether: (a) if A is convex then B is convex or not. (b) if B is convex then A is convex or not. (4) Let R be a field of real numbers and X=R, X is a vector space over R show that by definition the norms/II.II, and II.112 on X are equivalent where Ilxll₁ = max(lx,l, i=1,2,...,n) and llxll₂=(x²). oper (5) Let Ⓡ be a field of real numbers, Ⓡis a normed space under usual operations and norm, let E=(2,5,8), find int(E), b(E) and D(E). (6) Write the definition of bounded linear function between two normed spaces and write with prove the relation between continuous and bounded linear function between two normed spaces.arrow_forward
- ind → 6 Q₁/(a) Let R be a field of real numbers and X-P(x)=(a+bx+cx²+dx/ a,b,c,dER},X is a vector space over R, show that is finite dimension. (b) Let be a bijective linear function from a finite dimension vector ✓ into a space Yand Sbe a basis for X, show that whether f(S) basis for or not. (c) Let be a vector space over a field F and A,B)affine subsets of X,show that whether aAn BB, aAU BB be affine subsets of X or not, a,ẞ EF. (12 Jal (answer only two) (6) Let M be a non-empty subset of a vector space X and tEX, show that M is a hyperspace of X iff t+M is a hyperplane of X and tЄt+M. (b) State Jahn-Banach theorem and write with prove an application of Hahn-arrow_forward(b) Let A and B be two subset of a linear space X such that ACB, show that whether if A is affine set then B affine or need not and if B affine set then A affine set or need not. Qz/antonly be a-Show that every hyperspace of a vecor space X is hyperplane but the convers need not to be true. b- Let M be a finite dimension subspace of a Banach space X show that M is closed set. c-Show that every two norms on finite dimension vector space are equivant (1) Q/answer only two a-Write the definition of bounded set in: a normed space and write with prove an equivalent statement to a definition. b- Let f be a function from a normed space X into a normed space Y, show that f continuous iff f is bounded. c-Show that every finite dimension normed space is a Banach. Q/a- Let A and B two open sets in a normed space X, show that by definition AnB and AUB are open sets. (1 nood truearrow_forwardlog (6x+5)-log 3 = log 2 - log xarrow_forward
- 1 The ratio of Argan to Potassium from a sample found sample found in Canada is .195 Find The estimated age of the sample A In (1+8.33 (+)) t = (1-26 × 109) en (1 In aarrow_forward7. Find the doubling time of an investment earning 2.5% interest compounded a) semiannually b) continuouslyarrow_forward6. Find the time it will take $1000 to grow to $5000 at an interest rate of 3.5% if the interest is compounded a) quarterly b) continuouslyarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
What is Ellipse?; Author: Don't Memorise;https://www.youtube.com/watch?v=nzwCInIMlU4;License: Standard YouTube License, CC-BY