
a.
Find the regression line for the variables fracture toughness
Test whether there is enough evidence to conclude that the predictor variable mode-mixity angle is useful for predicting the value of the response variable fracture toughness.
a.
Answer to Problem 76SE
The regression line for the variables fracture toughness
There is sufficient evidence to conclude that the predictor variable mode-mixity angle is useful for predicting the value of the response variable fracture toughness.
Explanation of Solution
Given info:
The data represents the values of the variables fracture toughness
Calculation:
Linear regression model:
A linear regression model is given as
A linear regression model is given as
Regression:
Software procedure:
Step by step procedure to obtain regression equation using MINITAB software is given as,
- Choose Stat > Regression > Fit Regression Line.
- In Response (Y), enter the column of Fracture toughness.
- In Predictor (X), enter the column of Mode-mixity angle.
- Click OK.
The output using MINITAB software is given as,
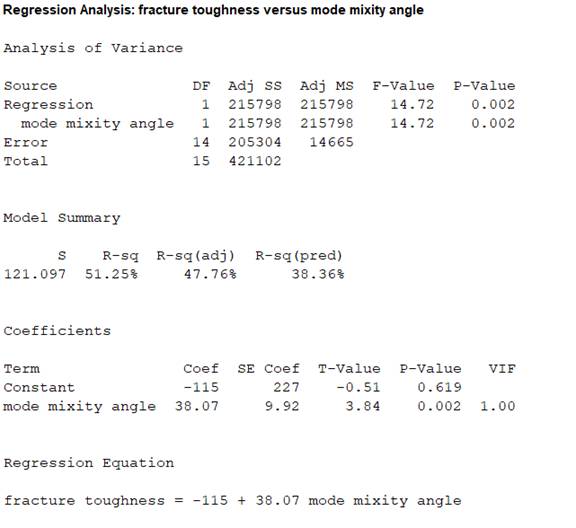
From the MINITAB output, the regression line is
Thus, the regression line for the variables fracture toughness
Interpretation:
The slope estimate implies an increase in fracture toughness by 38.07
The test hypotheses are given below:
Null hypothesis:
That is, there is no useful relationship between the variables fracture toughness
Alternative hypothesis:
That is, there is useful relationship between the variables fracture toughness
T-test statistic:
The test statistic is,
From the MINITAB output, the test statistic is 3.84 and the P-value is 0.002.
Thus, the value of test statistic is 3.84 and P-value is 0.002.
Level of significance:
Here, level of significance is not given.
So, the prior level of significance
Decision rule based on p-value:
If
If
Conclusion:
The P-value is 0.002 and
Here, P-value is less than the
That is
By the rejection rule, reject the null hypothesis.
Thus, there is enough evidence to conclude that the predictor variable mode-mixity angle is useful for predicting the value of the response variable fracture toughness.
b.
Test whether there is enough evidence to conclude that the change in fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50
b.
Answer to Problem 76SE
There is no sufficient evidence to conclude that the change in fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50
Explanation of Solution
Calculation:
From the MINITAB output obtained in part (a), the slope coefficient of the regression equation is
Here,
Claim:
Here, the claim is that the true average change in the fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50
The test hypotheses are given below:
Null hypothesis:
That is, the average change in the fracture toughness associated with 1 degree increase in mode-mixity angle is less than or equal to 50
Alternative hypothesis:
That is, the average change in the fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50
Test statistic:
The test statistic is,
Degrees of freedom:
The number of concrete beams that are sampled is
The degrees of freedom is,
Thus, the degree of freedom is 14.
Level of significance:
Here, level of significance is not given.
So, the prior level of significance
Critical value:
Software procedure:
Step by step procedure to obtain the critical value using the MINITAB software:
- Choose Graph > Probability Distribution Plot choose View Probability > OK.
- From Distribution, choose ‘t’ distribution and enter 14 as degrees of freedom.
- Click the Shaded Area tab.
- Choose Probability Value and Right Tail for the region of the curve to shade.
- Enter the Probability value as 0.05.
- Click OK.
Output using the MINITAB software is given below:
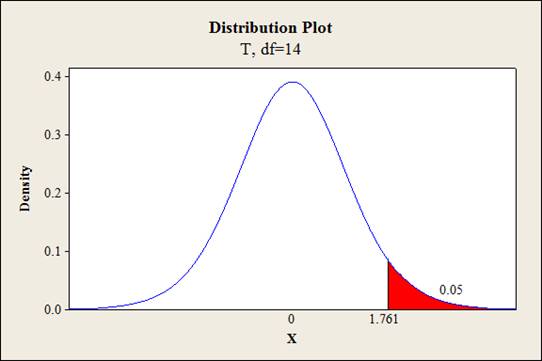
From the output, the critical value is 1.761.
Thus, the critical value is
From the MINITAB output obtained in part (a), the estimate of error standard deviation of slope coefficient is
Test statistic under null hypothesis:
Under the null hypothesis, the test statistic is obtained as follows:
Thus, the test statistic is -1.2026.
Decision criteria for the classical approach:
If
Conclusion:
Here, the test statistic is -1.2026 and critical value is 1.761.
The t statistic is less than the critical value.
That is,
Thus, the decision rule is, failed to reject the null hypothesis.
Hence, the average change in the fracture toughness associated with 1 degree increase in mode-mixity angle is less than or equal to 50
Therefore, there is no sufficient evidence to conclude that the change in fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50
c.
Explain whether the new observations of the variable mode-mixity angle give more precise estimate of slope coefficient than the actual observations.
c.
Answer to Problem 76SE
No, the new observations of the variable mode-mixity angle do not give more precise estimate of slope coefficient than the actual observations.
Explanation of Solution
Given info:
The data represents the new values of the variable mode-mixity angle, at which the response variable fracture toughness is predicted.
Calculation:
Confidence interval:
The general formula for the confidence interval for the slope of the regression line is,
Where,
The precision of the confidence interval increases with the decrease in the error standard deviation of the slope.
That is, the precision will be high for lower value of
Error sum of square: (SSE)
The variation in the observed values of the response variable that is not explained by the regression is defined as the regression sum of squares. The formula for error sum of square is
Estimate of error standard deviation of slope coefficient:
The general formula for the estimate of error standard deviation of slope coefficient is,
The defining formula for
Here, the estimate of error standard deviation of slope coefficient depends on the value of
The estimate of error standard deviation of slope coefficient decreases with the increase in the value of
The margin of error is product of critical value and standard error of the statistic. The higher width of the confidence interval indicates larger standard error of statistic. Hence, the margin of error also increases.
Therefore, the width of the confidence interval decreases with the decrease in value of error standard deviation. In other words it can be said that the precision decreases with the decrease in the value of
The value of
| 1 | 16.52 | 272.9104 |
| 2 | 17.53 | 307.3009 |
| 3 | 18.05 | 325.8025 |
| 4 | 18.05 | 325.8025 |
| 5 | 22.39 | 501.3121 |
| 6 | 23.89 | 570.7321 |
| 7 | 25.50 | 650.25 |
| 8 | 24.89 | 619.5121 |
| 9 | 23.48 | 551.3104 |
| 10 | 24.98 | 624.0004 |
| 11 | 25.55 | 652.8025 |
| 12 | 25.90 | 670.81 |
| 13 | 22.65 | 513.0225 |
| 14 | 23.69 | 561.2161 |
| 15 | 24.15 | 583.2225 |
| 16 | 24.45 | 597.8025 |
| Total |
Here,
Thus, the value of
Hence, the covariance is
The value of
| 1 | 16 | 256 |
| 2 | 16 | 256 |
| 3 | 18 | 324 |
| 4 | 18 | 324 |
| 5 | 20 | 400 |
| 6 | 20 | 400 |
| 7 | 20 | 400 |
| 8 | 20 | 400 |
| 9 | 22 | 484 |
| 10 | 22 | 484 |
| 11 | 22 | 484 |
| 12 | 22 | 484 |
| 13 | 24 | 576 |
| 14 | 24 | 576 |
| 15 | 26 | 676 |
| 16 | 26 | 676 |
| Total |
Here,
Thus, the value of
Hence, the covariance is
The value of
That is,
Hence, the estimate of error standard deviation of slope coefficient is lower for old observations.
Therefore, the precision is high for old observations.
Thus, the new observations of the variable mode-mixity angle do not give more precise estimate of slope coefficient than the actual observations.
d.
Find the
Find the prediction interval of fracture toughness for a single sandwich panel of 18 degrees mode-mixity angle.
Find the interval estimate for the true mean fracture toughness of all sandwich panels with 22 degrees mode-mixity angle.
Find the prediction interval of fracture toughness for a single sandwich panel of 22 degrees mode-mixity angle.
d.
Answer to Problem 76SE
The 95% specified confidence interval for the true mean fracture toughness of all sandwich panels with 18 degrees mode-mixity angle is
The 95% prediction interval of fracture toughness for a single sandwich panel with 18 degrees mode-mixity angle is
The 95% specified confidence interval for the true mean fracture toughness of all sandwich panels with 22 degrees mode-mixity angle is
The 95% prediction interval of fracture toughness for a single sandwich panel with 22 degrees mode-mixity angle is
Explanation of Solution
Calculation:
Here, the regression equation is
Expected fracture toughness when the mode-mixity angle is 18 degrees:
The expected fracture toughness with 18 degrees mode-mixity angle is obtained as follows:
Thus, the expected fracture toughness with 18 degrees mode-mixity angle is 570.26.
95% confidence interval of true mean fracture tough for an angle of 18 degrees:
The general formula for the
Where,
From the MINITAB output in part (a), the value of the standard error of the estimate is
The value of
| 1 | 16.52 | 272.9104 |
| 2 | 17.53 | 307.3009 |
| 3 | 18.05 | 325.8025 |
| 4 | 18.05 | 325.8025 |
| 5 | 22.39 | 501.3121 |
| 6 | 23.89 | 570.7321 |
| 7 | 25.50 | 650.25 |
| 8 | 24.89 | 619.5121 |
| 9 | 23.48 | 551.3104 |
| 10 | 24.98 | 624.0004 |
| 11 | 25.55 | 652.8025 |
| 12 | 25.90 | 670.81 |
| 13 | 22.65 | 513.0225 |
| 14 | 23.69 | 561.2161 |
| 15 | 24.15 | 583.2225 |
| 16 | 24.45 | 597.8025 |
| Total |
Here,
The mean mode-mixity angle is,
Thus, the mean mode-mixity angle is
Covariance term
Thus, the value of
Hence, the covariance is
Since, the level of confidence is not specified. The prior confidence level 95% can be used.
Critical value:
For 95% confidence level,
Degrees of freedom:
The sample size is
The degrees of freedom is,
From Table A.5 of the t-distribution in Appendix A, the critical value corresponding to the right tail area 0.025 and 14 degrees of freedom is 2.145.
Thus, the critical value is
The 95% confidence interval is,
Thus, the 95% specified confidence interval for the true mean fracture toughness of all sandwich panels with 18 degrees mode-mixity angle is
Interpretation:
There is 95% confident that, the true mean fracture toughness of all sandwich panels with 18 degrees mode-mixity angle lies between 453.6507 and 686.8693.
95% prediction interval of fracture tough for an angle of 18 degrees:
Prediction interval for a single future value:
Prediction interval is used to predict a single value of the focus variable that is to be observed at some future time. In other words it can be said that the prediction interval gives a single future value rather than estimating the mean value of the variable.
The general formula for
where
The 95% prediction interval is,
Thus, the 95% prediction interval of fracture toughness for a single sandwich panel with 18 degrees mode-mixity angle is
Interpretation:
For repeated samples, there is 95% confident that the fracture toughness for a single sandwich panel with 18 degrees mode-mixity angle lies between 285.5331 and 854.9569.
Expected fracture toughness when the mode-mixity angle is 22 degrees:
The expected fracture toughness with 22 degrees mode-mixity angle is obtained as follows:
Thus, the expected fracture toughness with 22 degrees mode-mixity angle is 722.54.
95% confidence interval of true mean fracture tough for an angle of 22 degrees:
The 95% confidence interval is,
Thus, the 95% specified confidence interval for the true mean fracture toughness of all sandwich panels with 22 degrees mode-mixity angle is
Interpretation:
There is 95% confident that, the true mean fracture toughness of all sandwich panels with 22 degrees mode-mixity angle lies between 656.3689 and 788.7111.
95% prediction interval of fracture tough for an angle of 22 degrees:
The 95% prediction interval is,
Thus, the 95% prediction interval of fracture toughness for a single sandwich panel with 22 degrees mode-mixity angle is
Interpretation:
For repeated samples, there is 95% confident that the fracture toughness for a single sandwich panel with 22 degrees mode-mixity angle lies between 454.491 and 990.589.
Want to see more full solutions like this?
Chapter 12 Solutions
PROBABILITY & STATS FOR ENGINEERING &SCI
- High Cholesterol: A group of eight individuals with high cholesterol levels were given a new drug that was designed to lower cholesterol levels. Cholesterol levels, in milligrams per deciliter, were measured before and after treatment for each individual, with the following results: Individual Before 1 2 3 4 5 6 7 8 237 282 278 297 243 228 298 269 After 200 208 178 212 174 201 189 185 Part: 0/2 Part 1 of 2 (a) Construct a 99.9% confidence interval for the mean reduction in cholesterol level. Let a represent the cholesterol level before treatment minus the cholesterol level after. Use tables to find the critical value and round the answers to at least one decimal place.arrow_forwardI worked out the answers for most of this, and provided the answers in the tables that follow. But for the total cost table, I need help working out the values for 10%, 11%, and 12%. A pharmaceutical company produces the drug NasaMist from four chemicals. Today, the company must produce 1000 pounds of the drug. The three active ingredients in NasaMist are A, B, and C. By weight, at least 8% of NasaMist must consist of A, at least 4% of B, and at least 2% of C. The cost per pound of each chemical and the amount of each active ingredient in one pound of each chemical are given in the data at the bottom. It is necessary that at least 100 pounds of chemical 2 and at least 450 pounds of chemical 3 be used. a. Determine the cheapest way of producing today’s batch of NasaMist. If needed, round your answers to one decimal digit. Production plan Weight (lbs) Chemical 1 257.1 Chemical 2 100 Chemical 3 450 Chemical 4 192.9 b. Use SolverTable to see how much the percentage of…arrow_forwardAt the beginning of year 1, you have $10,000. Investments A and B are available; their cash flows per dollars invested are shown in the table below. Assume that any money not invested in A or B earns interest at an annual rate of 2%. a. What is the maximized amount of cash on hand at the beginning of year 4.$ ___________ A B Time 0 -$1.00 $0.00 Time 1 $0.20 -$1.00 Time 2 $1.50 $0.00 Time 3 $0.00 $1.90arrow_forward
- For each of the time series, construct a line chart of the data and identify the characteristics of the time series (that is, random, stationary, trend, seasonal, or cyclical). Year Month Rate (%)2009 Mar 8.72009 Apr 9.02009 May 9.42009 Jun 9.52009 Jul 9.52009 Aug 9.62009 Sep 9.82009 Oct 10.02009 Nov 9.92009 Dec 9.92010 Jan 9.82010 Feb 9.82010 Mar 9.92010 Apr 9.92010 May 9.62010 Jun 9.42010 Jul 9.52010 Aug 9.52010 Sep 9.52010 Oct 9.52010 Nov 9.82010 Dec 9.32011 Jan 9.12011 Feb 9.02011 Mar 8.92011 Apr 9.02011 May 9.02011 Jun 9.12011 Jul 9.02011 Aug 9.02011 Sep 9.02011 Oct 8.92011 Nov 8.62011 Dec 8.52012 Jan 8.32012 Feb 8.32012 Mar 8.22012 Apr 8.12012 May 8.22012 Jun 8.22012 Jul 8.22012 Aug 8.12012 Sep 7.82012 Oct…arrow_forwardFor each of the time series, construct a line chart of the data and identify the characteristics of the time series (that is, random, stationary, trend, seasonal, or cyclical). Date IBM9/7/2010 $125.959/8/2010 $126.089/9/2010 $126.369/10/2010 $127.999/13/2010 $129.619/14/2010 $128.859/15/2010 $129.439/16/2010 $129.679/17/2010 $130.199/20/2010 $131.79 a. Construct a line chart of the closing stock prices data. Choose the correct chart below.arrow_forwardFor each of the time series, construct a line chart of the data and identify the characteristics of the time series (that is, random, stationary, trend, seasonal, or cyclical) Date IBM9/7/2010 $125.959/8/2010 $126.089/9/2010 $126.369/10/2010 $127.999/13/2010 $129.619/14/2010 $128.859/15/2010 $129.439/16/2010 $129.679/17/2010 $130.199/20/2010 $131.79arrow_forward
- 1. A consumer group claims that the mean annual consumption of cheddar cheese by a person in the United States is at most 10.3 pounds. A random sample of 100 people in the United States has a mean annual cheddar cheese consumption of 9.9 pounds. Assume the population standard deviation is 2.1 pounds. At a = 0.05, can you reject the claim? (Adapted from U.S. Department of Agriculture) State the hypotheses: Calculate the test statistic: Calculate the P-value: Conclusion (reject or fail to reject Ho): 2. The CEO of a manufacturing facility claims that the mean workday of the company's assembly line employees is less than 8.5 hours. A random sample of 25 of the company's assembly line employees has a mean workday of 8.2 hours. Assume the population standard deviation is 0.5 hour and the population is normally distributed. At a = 0.01, test the CEO's claim. State the hypotheses: Calculate the test statistic: Calculate the P-value: Conclusion (reject or fail to reject Ho): Statisticsarrow_forward21. find the mean. and variance of the following: Ⓒ x(t) = Ut +V, and V indepriv. s.t U.VN NL0, 63). X(t) = t² + Ut +V, U and V incepires have N (0,8) Ut ①xt = e UNN (0162) ~ X+ = UCOSTE, UNNL0, 62) SU, Oct ⑤Xt= 7 where U. Vindp.rus +> ½ have NL, 62). ⑥Xn = ΣY, 41, 42, 43, ... Yn vandom sample K=1 Text with mean zen and variance 6arrow_forwardA psychology researcher conducted a Chi-Square Test of Independence to examine whether there is a relationship between college students’ year in school (Freshman, Sophomore, Junior, Senior) and their preferred coping strategy for academic stress (Problem-Focused, Emotion-Focused, Avoidance). The test yielded the following result: image.png Interpret the results of this analysis. In your response, clearly explain: Whether the result is statistically significant and why. What this means about the relationship between year in school and coping strategy. What the researcher should conclude based on these findings.arrow_forward
- A school counselor is conducting a research study to examine whether there is a relationship between the number of times teenagers report vaping per week and their academic performance, measured by GPA. The counselor collects data from a sample of high school students. Write the null and alternative hypotheses for this study. Clearly state your hypotheses in terms of the correlation between vaping frequency and academic performance. EditViewInsertFormatToolsTable 12pt Paragrapharrow_forwardA smallish urn contains 25 small plastic bunnies – 7 of which are pink and 18 of which are white. 10 bunnies are drawn from the urn at random with replacement, and X is the number of pink bunnies that are drawn. (a) P(X = 5) ≈ (b) P(X<6) ≈ The Whoville small urn contains 100 marbles – 60 blue and 40 orange. The Grinch sneaks in one night and grabs a simple random sample (without replacement) of 15 marbles. (a) The probability that the Grinch gets exactly 6 blue marbles is [ Select ] ["≈ 0.054", "≈ 0.043", "≈ 0.061"] . (b) The probability that the Grinch gets at least 7 blue marbles is [ Select ] ["≈ 0.922", "≈ 0.905", "≈ 0.893"] . (c) The probability that the Grinch gets between 8 and 12 blue marbles (inclusive) is [ Select ] ["≈ 0.801", "≈ 0.760", "≈ 0.786"] . The Whoville small urn contains 100 marbles – 60 blue and 40 orange. The Grinch sneaks in one night and grabs a simple random sample (without replacement) of 15 marbles. (a)…arrow_forwardSuppose an experiment was conducted to compare the mileage(km) per litre obtained by competing brands of petrol I,II,III. Three new Mazda, three new Toyota and three new Nissan cars were available for experimentation. During the experiment the cars would operate under same conditions in order to eliminate the effect of external variables on the distance travelled per litre on the assigned brand of petrol. The data is given as below: Brands of Petrol Mazda Toyota Nissan I 10.6 12.0 11.0 II 9.0 15.0 12.0 III 12.0 17.4 13.0 (a) Test at the 5% level of significance whether there are signi cant differences among the brands of fuels and also among the cars. [10] (b) Compute the standard error for comparing any two fuel brands means. Hence compare, at the 5% level of significance, each of fuel brands II, and III with the standard fuel brand I. [10] �arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





