
Exercises 49 and 50 refer to the Menger sponge, a three-dimensional cousin of the Sierpinski gasket. The Menger sponge is defined by the following recursive construction rule.
Menger Sponge
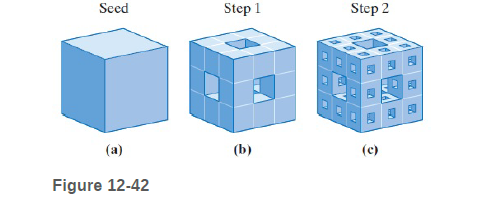
• Start. Start with a solid seed cube [Fig. 12-42(a)].
• Step 1. Subdivide the seed cube into 27 equal subcubes and remove the central cube and the six cubes in the centers of each face. This leaves a "sponge" consisting of 20 solid subcubes, as shown in Fig. 12-42(b)0.
• Step 2. Subdivide each solid subcube into 27 subcubes and remove the central cube and the six cubes in the centers of each face. This gives the "sponge" shown in Fig. 12-42(c). (Call the procedure of removing the central cube and the cubes in the center of each face procedure MS.)
• Steps 3, 4, etc. Apply procedure MS to each cube of the "sponge" obtained in the previous step.
Let H denote the total number of cubic holes obtained at a particular step of the construction of the Menger sponge.
a. Complete the entries in the following table.
| H | |
| Start | 0 |
| Step 1 | 7 |
| Step 2 |
|
| Step 3 | |
| Step 4 | |
| Step 5 |
b. Find a formula that gives the value of H for the sponge obtained at step N of the construction (Hint you will need to use the geometric sum formula from chapter 9)
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
Excursions in Modern Mathematics, Books a la carte edition (9th Edition)
- (6) ≤ a) Determine the following groups: Homz(Q, Z), Homz(Q, Q), Homz(Q/Z, Z) for n E N. Homz(Z/nZ, Q) b) Show for ME MR: HomR (R, M) = M.arrow_forwardAlready got wrong chatgpt answer Plz don't use chatgpt answer will upvote otherwise leave it .arrow_forwardy=f'(x) 1 8 The function f is defined on the closed interval [0,8]. The graph of its derivative f' is shown above. How many relative minima are there for f(x)? O 2 6 4 00arrow_forward
- 60! 5!.7!.15!.33!arrow_forwardUse Euler's summation formula to prove that, for x > 2, Σ log n n3 = A log x 2x2 n≤x where A is a constant. - 1 +0 4x2 log x x3 "arrow_forward• • Let > be a potential for the vector field F = (−2 y³, −6 xy² − 4 z³, −12 yz² + 4 2). Then the value of sin((-1.63, 2.06, 0.57) – (0,0,0)) is - 0.336 -0.931 -0.587 0.440 0.902 0.607 -0.609 0.146arrow_forward
- 1. If f(x² + 1) = x + 5x² + 3, what is f(x² - 1)?arrow_forward2. What is the total length of the shortest path that goes from (0,4) to a point on the x-axis, then to a point on the line y = 6, then to (18.4)?arrow_forwardThe value of cos(4M) where M is the magnitude of the vector field with potential ƒ = e² sin(лy) cos(π²) at x = 1, y = 1/4, z = 1/3 is 0.602 -0.323 0.712 -0.816 0.781 0.102 0.075 0.013arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
