Chapter 1.2, Problem 44PPS

(a)

To determine

To write: two expressions to represent the number of registered dogs of the top four breeds.

Answer to Problem 44PPS

First pair:

  $\stackrel{a}{\overbrace{870,192}}\cdot \left(\stackrel{b}{\overbrace{\frac{14.2}{100}}}+\stackrel{c}{\overbrace{\frac{5.6}{100}}}\right)$

Second one would then be:

  $870,192\cdot \left(\frac{5.0}{100}+\frac{4.9}{100}\right)$

Explanation of Solution

Given information:

The chart shows the percent of dogs registered with the A.K club that are of the eight most popular breeds.

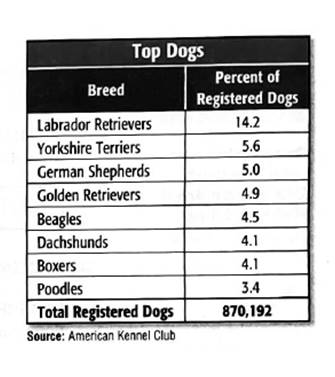
Calculation:

The distributive property rule states that:

  $a\cdot \left(b+c\right)=a\cdot b+a\cdot c$

If we want to apply this rule on given task and create two expressions, we need to make two pairs of dog breeds and use them with given distributivity rule to write down final solution.

First pair:

  $\stackrel{a}{\overbrace{870,192}}\cdot \left(\stackrel{b}{\overbrace{\frac{14.2}{100}}}+\stackrel{c}{\overbrace{\frac{5.6}{100}}}\right)$

Second one would then be:

  $870,192\cdot \left(\frac{5.0}{100}+\frac{4.9}{100}\right)$

(b)

To determine

To find: the number of registered dogs of the top four breeds.

Answer to Problem 44PPS

Final solution of total number of dogs is:

258445.

Explanation of Solution

Given information:

The chart shows the percent of dogs registered with the A.K club that are of the eight most popular breeds.

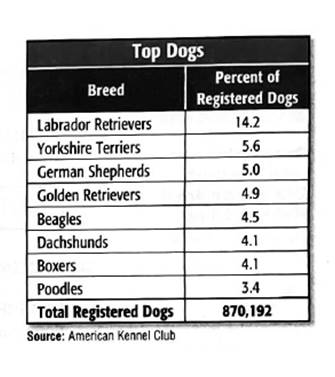
Calculation:

The distributive property rule states that:

  $a\cdot \left(b+c\right)=a\cdot b+a\cdot c$

If we want to apply this rule on given task and create two expressions, we need to make two pairs of dog breeds and use them with given distributivity rule to write down final solution.

First pair:

  $\begin{array}{c}\stackrel{a}{\overbrace{870,192}}\cdot \left(\stackrel{b}{\overbrace{\frac{14.2}{100}}}+\stackrel{c}{\overbrace{\frac{5.6}{100}}}\right)=\stackrel{a-b}{\overbrace{123,567}}+\stackrel{a-c}{\overbrace{48730}}\\ =172297\end{array}$

Second one would then be:

  $\begin{array}{c}870,192\cdot \left(\frac{5.0}{100}+\frac{4.9}{100}\right)=43509+42639\\ =86148\end{array}$

Final solution of total number of dogs is:

258445.