Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
10th Edition
ISBN: 9781337888585
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 12, Problem 41AP
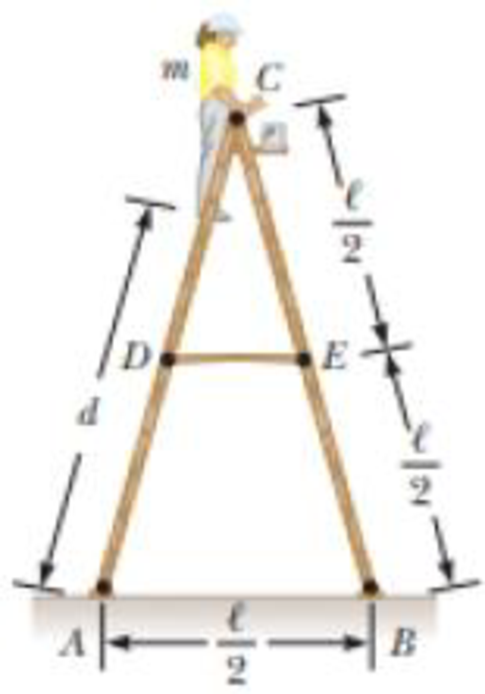
A stepladder of negligible weight is constructed as shown in Figure P12.40, with AC = BC = ℓ. A painter of mass m stands on the ladder a distance d from the bottom. Assuming the floor is frictionless, find (a) the tension in the horizontal bar DE connecting the two halves of the ladder, (b) the normal forces at A and B, and (c) the components of the reaction force at the single hinge C that the left half of the ladder exerts on the right half. Suggestion: Treat the ladder as a single object, but also treat each half of the ladder separately.
Figure P12.40 Problems 40 and 41.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
I need correct answer not chatgpt
What is the resistance (in (2) of a 27.5 m long piece of 17 gauge copper wire having a 1.150 mm diameter?
0.445
ΧΩ
Find the ratio of the diameter of silver to iron wire, if they have the same resistance per unit length (as they might in household wiring).
d.
Ag
dFe
= 2.47
×
Chapter 12 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
Ch. 12.1 - Consider the object subject to the two forces of...Ch. 12.1 - Consider the object subject to the three forces in...Ch. 12.2 - A meterstick of uniform density is hung from a...Ch. 12.4 - For the three parts of this Quick Quiz, choose...Ch. 12 - You are building additional storage space in your...Ch. 12 - Why is the following situation impossible? A...Ch. 12 - Prob. 3PCh. 12 - A circular pizza of radius R has a circular piece...Ch. 12 - Your brother is opening a skateboard shop. He has...Ch. 12 - A uniform beam of length 7.60 m and weight 4.50 ...
Ch. 12 - Prob. 7PCh. 12 - A uniform beam of length L and mass m shown in...Ch. 12 - A flexible chain weighing 40.0 N hangs between two...Ch. 12 - A 20.0-kg floodlight in a park is supported at the...Ch. 12 - Prob. 11PCh. 12 - Review. While Lost-a-Lot ponders his next move in...Ch. 12 - Figure P12.13 shows a claw hammer being used to...Ch. 12 - A 10.0-kg monkey climbs a uniform ladder with...Ch. 12 - John is pushing his daughter Rachel in a...Ch. 12 - Prob. 16PCh. 12 - The deepest point in the ocean is in the Mariana...Ch. 12 - A steel wire of diameter 1 mm can support a...Ch. 12 - A child slides across a floor in a pair of...Ch. 12 - Evaluate Youngs modulus for the material whose...Ch. 12 - Prob. 21PCh. 12 - When water freezes, it expands by about 9.00%....Ch. 12 - Review. A 30.0-kg hammer, moving with speed 20.0...Ch. 12 - A uniform beam resting on two pivots has a length...Ch. 12 - A bridge of length 50.0 m and mass 8.00 104 kg is...Ch. 12 - Prob. 26APCh. 12 - The lintel of prestressed reinforced concrete in...Ch. 12 - Prob. 28APCh. 12 - A hungry bear weighing 700 N walks out on a beam...Ch. 12 - Prob. 30APCh. 12 - A uniform sign of weight Fg and width 2L hangs...Ch. 12 - When a person stands on tiptoe on one foot (a...Ch. 12 - A 10 000-N shark is supported by a rope attached...Ch. 12 - Assume a person bends forward to lift a load with...Ch. 12 - A uniform beam of mass m is inclined at an angle ...Ch. 12 - Prob. 36APCh. 12 - When a circus performer performing on the rings...Ch. 12 - Figure P12.38 shows a light truss formed from...Ch. 12 - Prob. 39APCh. 12 - A stepladder of negligible weight is constructed...Ch. 12 - A stepladder of negligible weight is constructed...Ch. 12 - Review. A wire of length L, Youngs modulus Y, and...Ch. 12 - Two racquetballs, each having a mass of 170 g, are...Ch. 12 - Prob. 44APCh. 12 - Review. An aluminum wire is 0.850 m long and has a...Ch. 12 - You have been hired as an expert witness in a case...Ch. 12 - A 500-N uniform rectangular sign 4.00 m wide and...Ch. 12 - A steel cable 3.00 cm2 in cross-sectional area has...Ch. 12 - A uniform rod of weight Fg and length L is...Ch. 12 - In the What If? section of Example 12.2, let d...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Find the ratio of the diameter of silver to iron wire, if they have the same resistance per unit length (as they might in household wiring). d Ag = 2.51 dFe ×arrow_forwardShow that the units 1 v2/Q = 1 W, as implied by the equation P = V²/R. Starting with the equation P = V²/R, we can get an expression for a watt in terms of voltage and resistance. The units for voltage, V, are equivalent to [? v2 v2 A, are equivalent to J/C ✓ X . Therefore, 1 = 1 = 1 A V1 J/s Ω V-A X = 1 W. . The units for resistance, Q, are equivalent to ? The units for current,arrow_forwardPlease solve and answer the question correctly please. Thank you!!arrow_forward
- What is the equivalent resistance between points A and B of the network shown in the figure? A • 12 B 4.0 6.0 Ω 8.0 Ωarrow_forwardAccording to the provided information answer the question accorrding to grade 11 physics Jerry has decided to give up his part-time job for a new career, cat-burglar! Jerry loves the idea of dressing up like a cat all day and of course the chance of meeting Cat Woman! On Jerry's first "job" he figures out his escape plan. He travels 3.0 km south for 15 minutes and then 8.0 km west for 1.5 hours before reaching his house. Draw a sketch diagram of the path he took with all the appropriate labels.arrow_forwardPlease solve and answer all parts of the question correctly please. Thank you!!arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY