
Concept explainers
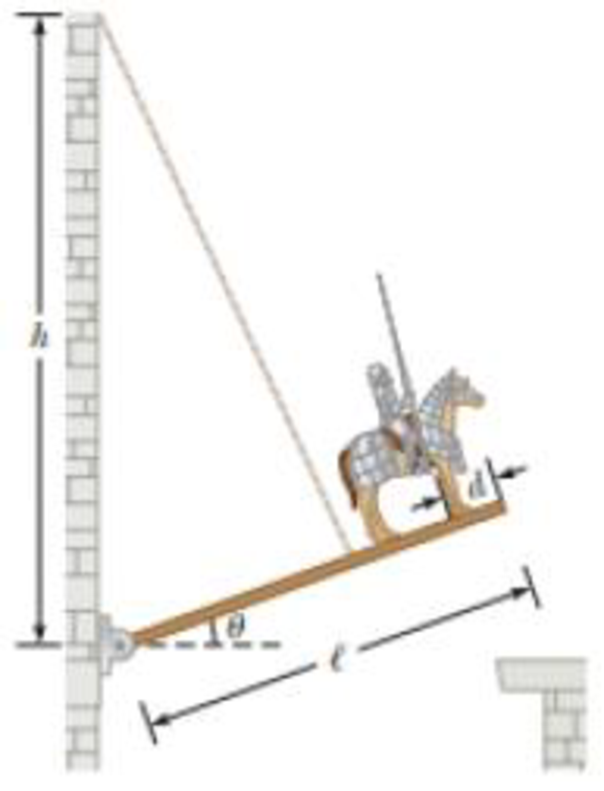
Review. While Lost-a-Lot ponders his next move in the situation described in Problem 11 and illustrated in Figure P12.11, the enemy attacks! An incoming projectile breaks off the stone ledge so that the end of the drawbridge can be lowered past the wall where it usually rests. In addition, a fragment of the projectile bounces up and cuts the drawbridge cable! The hinge between the castle wall and the bridge is frictionless, and the bridge swings down freely until it is vertical and smacks into the vertical castle wall below the castle entrance. (a) How long does Lost-a-Lot stay in contact with the bridge while it swings downward? (b) Find the
(a)
The time that Lost a Lot stay in contact with the bridge while it swings downward.
Answer to Problem 12P
The time that Lost a Lot stay in contact with the bridge while it swings downward is
Explanation of Solution
Given info: The length of the uniform bridge is
There is no time interval as the Lost a Lot stay in contact with the bridge while it swings downward because the horse feet loose contact with the down bridge as soon as it begins to move because the vertical acceleration act on the feet is greater than the acceleration due to gravity due to that the horse is in the air and moves upward with a vertical component of acceleration.
Conclusion:
Therefore, the time that Lost a Lot stay in contact with the bridge while it swings downward is
(b)
The angular acceleration of the bridge just as it starts to move.
Answer to Problem 12P
The angular acceleration of the bridge just as it starts to move is
Explanation of Solution
Given info: The length of the uniform bridge is
The mass moment of inertial along the centroid is,
The total moment along the centroid is,
Here,
Total moment along the centroid is,
Here,
Substitute
Substitute
Conclusion:
Therefore, the angular acceleration of the bridge just as it starts to move is
(c)
The angular speed of the bridge when it strikes the wall below the hinge.
Answer to Problem 12P
The angular speed of the bridge when it strikes the wall below the hinge is
Explanation of Solution
Given info: The length of the uniform bridge is
The total height of the wall from the point of hinge is,
Here,
From the conservation of energy, the total potential energy will be equal to the rotational energy is,
Here,
Substitute
Substitute
Conclusion:
Therefore, the angular speed of the bridge when it strikes the wall below the hinge is
(d)
The force exerted by the hinge on the bridge immediately after the cable breaks.
Answer to Problem 12P
The force exerted by the hinge on the bridge immediately after the cable breaks is
Explanation of Solution
Given info: The length of the uniform bridge is
From Figure (1), the tangential acceleration is,
Here,
Substitute
Thus, the tangential acceleration is
The acceleration along the horizontal is,
Here,
The acceleration along the vertical is,
Here,
Force along the horizontal direction is,
Here,
Substitute
Substitute
Thus, the force along the horizontal is
Force along the vertical is,
Here,
Substitute
Substitute
Thus, the vertical force is
The force exerted by the hinge on the bridge is,
Here,
Substitute
Conclusion:
Therefore, the force exerted by the hinge on the bridge immediately after the cable breaks is
(e)
The force exerted by the hinge on the bridge immediately before strikes the cable wall.
Answer to Problem 12P
The force exerted by the hinge on the bridge immediately before strikes the cable wall is
Explanation of Solution
Given info: The length of the uniform bridge is
The acceleration along the vertical is,
From Newton’s second law, the total force along the vertical is,
Substitute
Substitute
Conclusion:
Therefore, the force exerted by the hinge on the bridge immediately before strikes the cable wall is
Want to see more full solutions like this?
Chapter 12 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
- Lab Assignment #3 Vectors 2. Determine the magnitude and sense of the forces in cables A and B. 30° 30° 300KN 3. Determine the forces in members A and B of the following structure. 30° B 200kN Name: TA: 4. Determine the resultant of the three coplanar forces using vectors. F₁ =500N, F₂-800N, F, 900N, 0,-30°, 62-50° 30° 50° F₁ = 500N = 900N F₂ = 800Narrow_forwardLab Assignment #3 Vectors Name: TA: 1. With the equipment provided in the lab, determine the magnitude of vector A so the system is in static equilibrium. Perform the experiment as per the figure below and compare the calculated values with the numbers from the spring scale that corresponds to vector A. A Case 1: Vector B 40g Vector C 20g 0 = 30° Vector A = ? Case 2: Vector B 50g Vector C = 40g 0 = 53° Vector A ? Case 3: Vector B 50g Vector C 30g 0 = 37° Vector A = ?arrow_forwardThree point-like charges are placed at the corners of an equilateral triangle as shown in the figure. Each side of the triangle has a length of 20.0 cm, and the point (A) is located half way between q1 and q2 along the side. Find the magnitude of the electric field at point (A). Let q1=-1.30 µC, q2=-4.20µC, and q3= +4.30 µC. __________________ N/Carrow_forward
- Find the total capacitance in micro farads of the combination of capacitors shown in the figure below. 2.01 0.30 µF 2.5 µF 10 μF × HFarrow_forwardI do not understand the process to answer the second part of question b. Please help me understand how to get there!arrow_forwardRank the six combinations of electric charges on the basis of the electric force acting on 91. Define forces pointing to the right as positive and forces pointing to the left as negative. Rank in increasing order by placing the most negative on the left and the most positive on the right. To rank items as equivalent, overlap them. ▸ View Available Hint(s) [most negative 91 = +1nC 92 = +1nC 91 = -1nC 93 = +1nC 92- +1nC 93 = +1nC -1nC 92- -1nC 93- -1nC 91= +1nC 92 = +1nC 93=-1nC 91 +1nC 92=-1nC 93=-1nC 91 = +1nC 2 = −1nC 93 = +1nC The correct ranking cannot be determined. Reset Help most positivearrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





