
Concept explainers
Exercises 31 through 34 refer to a variation of the chaos game. In this game you start with a square ABCD with sides of length 27 as shown in Fig. 12-41 and a fair die that you will roll many times. When you roll a 1, choose vertex A; when you roll a 2, choose vertex B; when you roll a 3, choose vertex C; and when you roll a 4 choose vertex D. (When you roll a 5 or a 6, disregard the roll and roll again.) A sequence of rolls will generate a sequence of points
• Start. Roll the die. Mark the chosen vertex and call it
• Step 1. Roll the die again. From
• Steps 2, 3, etc. Each time you roll the die, mark the point two-thirds of the way between the previous point and the chosen vertex.
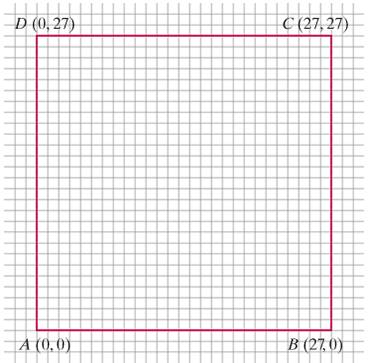
Figure 12-41
Using graph paper, find the points
a. the sequence of rolls 2, 2, 4, 4.
b. the sequence of rolls 2, 3, 4, 1.
c. the sequence of rolls 1, 3, 4, 1.
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
EBK EXCURSIONS IN MODERN MATHEMATICS
- numerical anaarrow_forward13. If X has the distribution function F(x) = 0 1 12 for x < -1 for -1x < 1 for 1x <3 2 3 for 3≤x≤5 4 1 for x≥5 find (a) P(X ≤3); (b) P(X = 3); (c) P(X < 3); (d) P(X≥1); (e) P(-0.4arrow_forwardTwo measurements are made of some quantity. For the first measurement, the average is 74.4528, the RMS error is 6.7441, and the uncertainty of the mean is 0.9264. For the second one, the average is 76.8415, the standard deviation is 8.3348, and the uncertainty of the mean is 1.1448. The expected value is exactly 75. 13. Express the first measurement in public notation. 14. Is there a significant difference between the two measurements? 1 15. How does the first measurement compare with the expected value? 16. How does the second measurement compare with the expected value?arrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answer .arrow_forwardIf you use any chatgpt will downvote.arrow_forwardPlease help I'm a working mom trying to help my son last minute (6th grader)! Need help with the blank ones and check the ones he got with full calculation so we can use it to study! Especially the mixed number fractions cause I'm rusty. Thanks in advance!arrow_forward|| 38 5층-11- 6 4 7 2 6arrow_forward4. Consider the initial value problem y' = 3x(y-1) 1/3, y(xo) = yo. (a) For what points (co, yo) does the IVP have a solution? (b) For what points (xo, yo) does the IVP have a unique solution on some open interval that contains 20? (c) Solve the IVP y' = 3x(y-1) 1/3, y(0) = 9 and determine the largest open interval on which this solution is unique.arrow_forwardFind the limit. (If the limit is infinite, enter 'oo' or '-o', as appropriate. If the limit does not otherwise exist, enter DNE.) lim X→ ∞ (✓ 81x2 - 81x + x 9x)arrow_forwardPlease solve the following Statistics and Probability Problem (show all work) : The probability that a patient recovers from a rare blood disease is 0.4 and 10 people are known to havecontracted this disease. Let X denote the random variable which denotes the number of patient who survivefrom the disease.1. Plot the probability mass function (pmf) of X.2. Plot the cumulative distribution function (cdf) of X.3. What is the probability that at least 8 survive, i.e., P {X ≥ 8}?4. What is the probability that 3 to 8 survive, i.e., P {3 ≤ X ≤ 8}?arrow_forwardthink about what you know about measurements. fill in each box. use words, numbers, and pictures. Show as many ideas as you can.arrow_forwardPlease solve the following Probability and Statistics problem (show all work and double check solution is correct): Suppose that a die is rolled twice. What are the possible values that the following random variables can take1. the maximum value to appear in the two rolls;2. the value of the first roll minus the value of the second roll?3. Calculate the probabilities associated with the above two random variables?arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
