Chapter 12, Problem 1RE

(a)

To determine

Whether the equation $4x-3y=12$ describes a line in ${ℝ}^3$.

Answer to Problem 1RE

The statement is false.

Explanation of Solution

Given:

The equation is $4x-3y=12$.

Calculation:

The graph of the given equation $4x-3y=12$ as shown below in Figure 1.

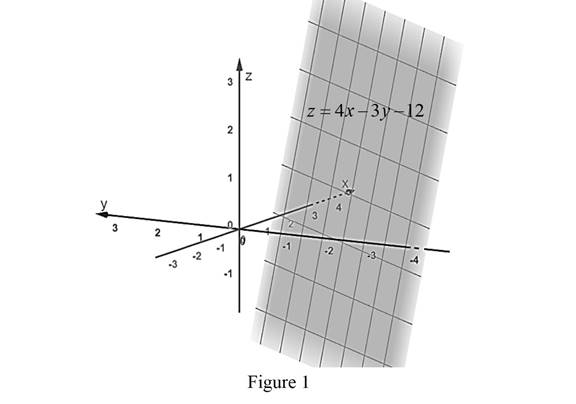
From Figure 1, it is observed that the given equation represents a plane in ${ℝ}^3$.

So, the given statement the equation $4x-3y=12$ describes a line in ${ℝ}^3$ does not satisfies.

Therefore, the statement is false.

(b)

To determine

Whether the equation $z^2=2x^2-6y^2$ satisfies z as a single function of x and y.

Answer to Problem 1RE

The statement is false.

Explanation of Solution

Given:

The equation is $z^2=2x^2-6y^2$.

Calculation:

The given equation is $z^2=2x^2-6y^2$.

If $2x^2-6y^2>0$ from the equation then the function of x and y is obtained.

Obtain the function in terms of x and y.

$\begin{array}{l}{z}^2=2x^2-6y^2\\ z=\pm \sqrt{2x^2-6y^2}\\ z=\sqrt{2x^2-6y^2},z=-\sqrt{2x^2-6y^2}\end{array}$

The functions are $z\left(x,y\right)=\sqrt{2x^2-6y^2}$ and $z\left(x,y\right)=-\sqrt{2x^2-6y^2}$ in terms of x and y.

Thus, z as a two function in terms of x and y.

Therefore, the statement is false.

(c)

To determine

Whether the function f satisfies the derivative $f_{xxy}=f_{yyx}$.

Answer to Problem 1RE

The statement is false.

Explanation of Solution

Let the function f has a continuous partial derivatives of all orders.

Then prove that $f_{xxy}=f_{yyx}$.

For example, assume $f\left(x,y\right)=x^{2}y$.

Obtain the value of $f_{xxy}$.

Take partial derivative of the function f with respect to x and obtain $f_x$.

$\begin{array}{c}{f}_x=\frac{\partial }{\partial x}\left(x^{2}y\right)\\ =y\frac{\partial }{\partial x}\left(x^2\right)\\ =y\left(2x\right)\\ =2xy\end{array}$

Thus, $f_x=2xy$ (1)

Take partial derivative of the equation (1) with respect to x and obtain $f_{xx}$.

$\begin{array}{c}{f}_{xx}=\frac{\partial }{\partial x}\left(2xy\right)\\ =2y\frac{\partial }{\partial x}\left(x\right)\\ =2y\left(1\right)\\ =2y\end{array}$

Hence, $f_{xx}=2y$ (2)

Again, take partial derivative for the equation (2) with respect to y and obtain $f_{xxy}$.

$\begin{array}{c}{f}_{xxy}=\frac{\partial }{\partial y}\left(2y\right)\\ =2\frac{\partial }{\partial y}\left(y\right)\\ =2\left(1\right)\\ =2\end{array}$

Therefore, $f_{xxy}=2$.

Obtain the value of $f_{yyx}$.

Take partial derivative of the function f with respect to y and obtain $f_y$.

$\begin{array}{c}{f}_y=\frac{\partial }{\partial y}\left(x^{2}y\right)\\ =x^2\frac{\partial }{\partial y}\left(y\right)\\ =x^2\left(1\right)\\ =x^2\end{array}$

Thus, $f_y=x^2$ (3)

Take partial derivative of the equation (1) with respect to y and obtain $f_{yy}$.

$\begin{array}{c}{f}_{yy}=\frac{\partial }{\partial y}\left(x^2\right)\\ =x^2\frac{\partial }{\partial y}\left(1\right)\\ =x^2\left(0\right)\\ =0\end{array}$

Hence, $f_{yy}=0$ (4)

Again, take partial derivative for the equation (2) with respect to x and obtain $f_{yyx}$.

$\begin{array}{c}{f}_{yyx}=\frac{\partial }{\partial x}\left(0\right)\\ =0\end{array}$

Therefore, $f_{yyx}=0$.

From above, it is concluded that $f_{xxy}=2\text{and}{f}_{yyx}=0$.

Thus, $f_{xxy}\ne f_{yyx}$.

Therefore, the statement is false.

(d)

To determine

Whether the gradient $\nabla f\left(a,b\right)$ lies in the plane tangent to the surface at $\left(a,b,f\left(a,b\right)\right)$.

Answer to Problem 1RE

The statement is false.

Explanation of Solution

Given:

The surface is $z=f\left(x,y\right)$.

Theorem used: The Gradient and Level Curves

“Given a function f differentiable at $\left(a,b\right)$, the line tangent to the level curve of f at $\left(a,b\right)$ is orthogonal to the gradient $\nabla f\left(a,b\right)$, provided $\nabla f\left(a,b\right)\ne 0$”.

Calculation:

The given surface is $z=f\left(x,y\right)$.

Assume the critical point be $\left(a,b\right)$.

Then, the given function is differentiable at $\left(a,b\right)$.

Thus, the gradient of $\nabla f\left(a,b\right)$ is calculated.

By above theorem, it can be concluded that the line tangent to the level curve of f at $\left(a,b\right)$ is orthogonal to the gradient $\nabla f\left(a,b\right)$.

But it does not satisfy the given statement. Because, it is given that the the gradient $\nabla f\left(a,b\right)$ lies in the plane tangent to the surface at $\left(a,b,f\left(a,b\right)\right)$.

Since, $\nabla f\left(a,b\right)$ lies in the xy- plane.

Therefore, the statement is false.

(e)

To determine

Whether the plane is always orthogonal to both the distinct intersecting planes.

Answer to Problem 1RE

The statement is true.

Explanation of Solution

Assume the equations of a plane.

The normal vector is calculated for an orthogonal plane and the two intersecting planes by taking the cross product.

Therefore, the statement is true.