
Concept explainers
Read bar graphs, line graphs, and circle graphs.
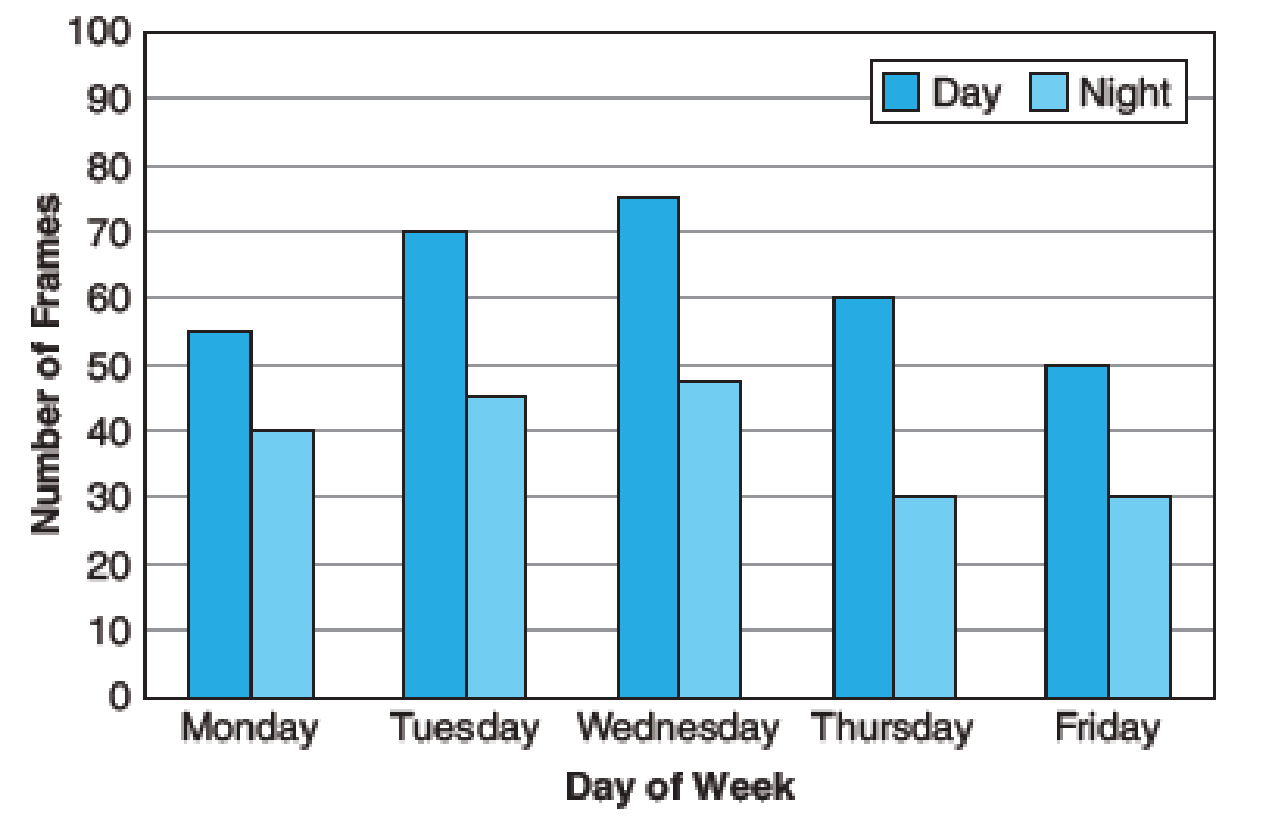
Trades Management From the bar graph below,
- (a) Determine the number of frames assembled by the Tuesday day shift. __________
- (b) Calculate the percent decrease in output from the Monday day shift to the Monday night shift. __________
Weekly Frame Assembly
Monthly Paint Jobs at Autobrite
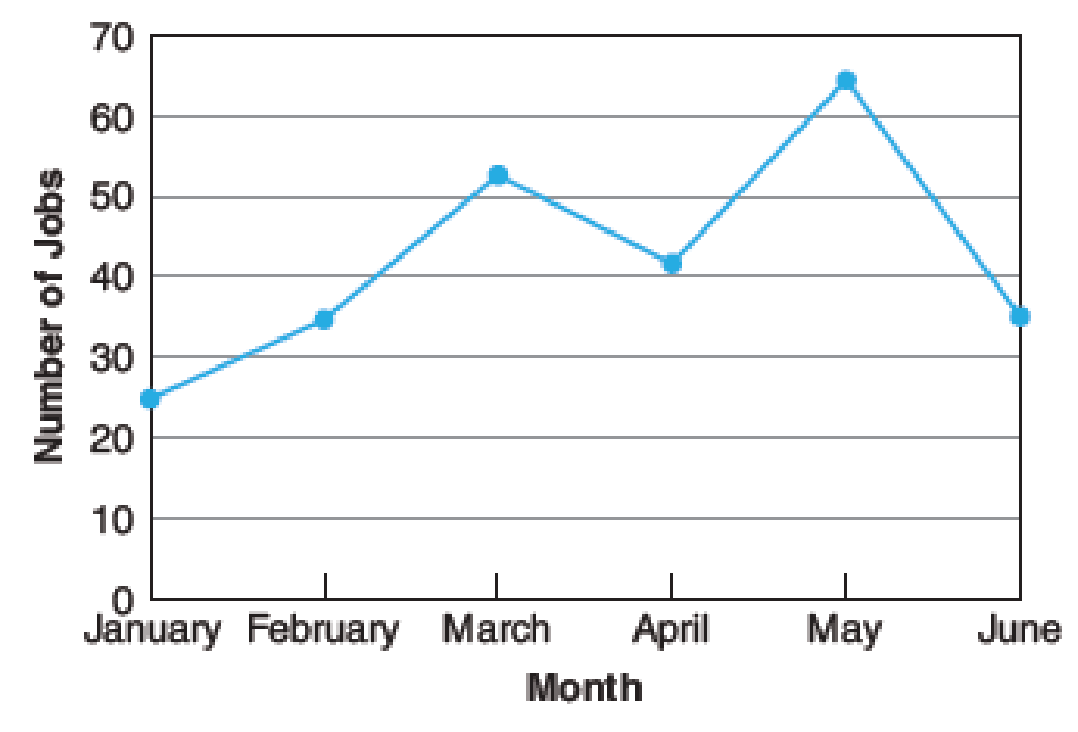
Problems (c) and (d) refer to the line graph above.
- (c) Determine the maximum number of paint jobs and the month during which they occurred. _________
- (d) Calculate the percent increase in the number of paint jobs from January to February. _________
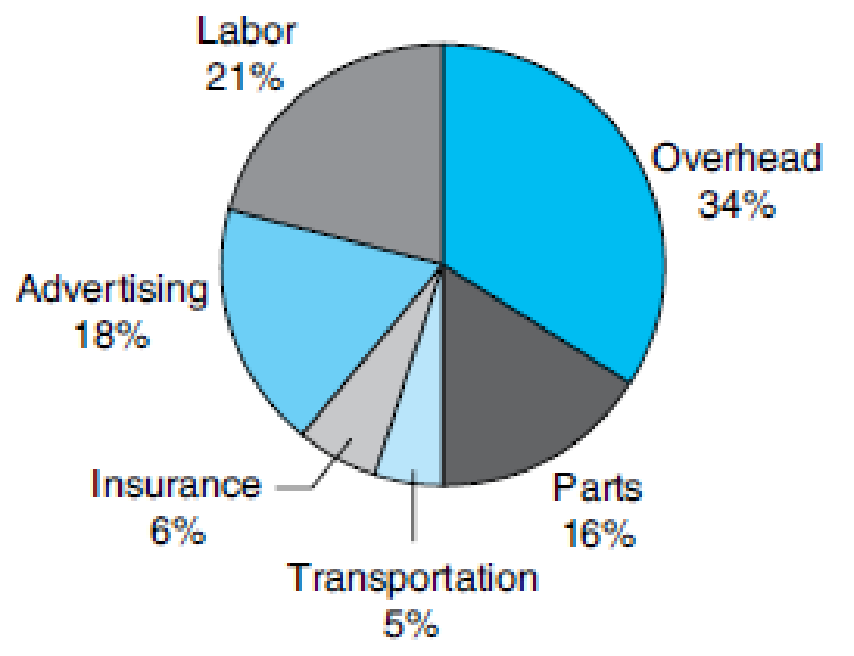
- (e) The average job for ABC Plumbing generates $227.50. Use the circle graph on the next page to calculate what portion of this amount is spent on advertising. _________
Percent of Business Expenditures
(a)
The number of frames assembled by the Tuesday day shift
Answer to Problem 1P
The number of frames assembled by the Tuesday day shift is
Explanation of Solution
Given:
The bar graph for the weekly frame assembly that is the number of frames in the day shift and night shift is mentioned.
Calculation:
From the bar graph, the height of the bar corresponding to the day of Tuesday for the day shift is 70. That is, there are 70 frames in the day shift.
Thus, the number of frames assembled by the Tuesday day shift is
(b)
The percent decrease in output from the Monday day shift to the Monday night shift
Answer to Problem 1P
The percent decrease in output from the Monday day shift to the Monday night shift is
Explanation of Solution
Formula used:
Percent change in proportion:
Calculation:
From the bar graph, the height of the bar corresponding to the day of Monday for the day shift is 55. That is, there are 55 frames in the day shift. The day of Monday for the night shift is 40. That is, there are 40 frames in the day shift.
The difference in frames is,
Substitute 55 as base and 15 as amount of decrease in the percent formula.
Thus, the percent decrease in output from the Monday day shift to the Monday night shift is
(c)
The maximum number of paint jobs and the month during which they occurred
Answer to Problem 1P
The maximum number of paint jobs is
The month during which maximum number of paint jobs occurred is
Explanation of Solution
Given:
The line graph of Monthly Paint Jobs at Autobrite is mentioned.
Calculation:
From the line graph it can be observed that the highest point of the paint jobs is 65 which correspond to the month of May. That is, the month of May has the highest jobs of 65.
Thus, the maximum number of paint jobs is
(d)
The percent increase in the number of paint jobs from January to February
Answer to Problem 1P
The percent increase in the number of paint jobs from January to February is
Explanation of Solution
From the line graph, the number of jobs corresponding to the month of January is 25 and the number of jobs corresponding to the month of February is 35.
The difference in jobs is,
Substitute 25 as base and 10 as amount of increase in the percent formula.
Thus, the percent increase in the number of paint jobs from January to February is
(e)
The portion of amount $227.50 that is spent on advertising based on the circle graph
Answer to Problem 1P
The portion of amount $227.50 that is spent on advertising based on the circle graph is
Explanation of Solution
Given:
The circle graph of Percent of Business Expenditures is mentioned. Also, average job for ABC Plumbing generates $227.50.
Calculation:
From the circle graph, the percentage of the business expenditure spent on advertising is 18%.
The amount is,
Thus, the portion of amount $227.50 that is spent on advertising based on the circle graph is
Want to see more full solutions like this?
Chapter 12 Solutions
Mathematics for the Trades: A Guided Approach (10th Edition) - Standalone book
- Find a polynomial with integer coefficients that satisfies the given conditions. T(x) has degree 4, zeros i and 1 + i, and constant term 12.arrow_forwardFind the absolute extrema of the function f(x, y) = x² + y² - 3x-3y+3 on the domain defined by x² + y² <9. Round answers to 3 decimals or more. Absolute Maximum: Absolute Minimum:arrow_forwardFind the maximum and minimum values of the function f(x, y) = e² subject to ï³ + y³ = 128 Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist. Maximum value:arrow_forward
- A chemical manufacturing plant can produce x units of chemical Z given p units of chemical P and 7 units of chemical R, where: z = 140p0.6,0.4 Chemical P costs $300 a unit and chemical R costs $1,500 a unit. The company wants to produce as many units of chemical Z as possible with a total budget of $187,500. A) How many units each chemical (P and R) should be "purchased" to maximize production of chemical Z subject to the budgetary constraint? Units of chemical P, p = Units of chemical R, r = B) What is the maximum number of units of chemical Z under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production, z= unitsarrow_forwardA firm manufactures a commodity at two different factories, Factory X and Factory Y. The total cost (in dollars) of manufacturing depends on the quantities, and y produced at each factory, respectively, and is expressed by the joint cost function: C(x, y) = x² + xy +4y²+400 A) If the company's objective is to produce 1,900 units per month while minimizing the total monthly cost of production, how many units should be produced at each factory? (Round your answer to whole units, i.e. no decimal places.) To minimize costs, the company should produce: units at Factory X and units at Factory Y B) For this combination of units, their minimal costs will be enter any commas in your answer.) Question Help: Video dollars. (Do notarrow_forwarduse Lagrange multipliers to solvearrow_forward
- Suppose a Cobb-Douglas Production function is given by the following: P(L,K)=80L0.75 K-0.25 where L is units of labor, K is units of capital, and P(L, K) is total units that can be produced with this labor/capital combination. Suppose each unit of labor costs $400 and each unit of capital costs $1,600. Further suppose a total of $384,000 is available to be invested in labor and capital (combined). A) How many units of labor and capital should be "purchased" to maximize production subject to your budgetary constraint? Units of labor, L = Units of capital, K = B) What is the maximum number of units of production under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production = unitsarrow_forwardSuppose a Cobb-Douglas Production function is given by the function: P(L, K) = 7L0.0 K0.4 Furthemore, the cost function for a facility is given by the function: C(L, K) = 100L +400K Suppose the monthly production goal of this facility is to produce 15,000 items. In this problem, we will assume L represents units of labor invested and K represents units of capital invested, and that you can invest in tenths of units for each of these. What allocation of labor and capital will minimize total production Costs? Units of Labor L = Units of Capital K = (Show your answer is exactly 1 decimal place) (Show your answer is exactly 1 decimal place) Also, what is the minimal cost to produce 15,000 units? (Use your rounded values for L and K from above to answer this question.) The minimal cost to produce 15,000 units is $ Hint: 1. Your constraint equation involves the Cobb Douglas Production function, not the Cost function. 2. When finding a relationship between L and K in your system of equations,…arrow_forward1. Give a subset that satisfies all the following properties simultaneously: Subspace Convex set Affine set Balanced set Symmetric set Hyperspace Hyperplane 2. Give a subset that satisfies some of the conditions mentioned in (1) but not all, with examples. 3. Provide a mathematical example (not just an explanation) of the union of two balanced sets that is not balanced. 4. What is the precise mathematical condition for the union of two hyperspaces to also be a hyperspace? Provide a proof. edited 9:11arrow_forward
- Find the absolute maximum and minimum of f(x, y) = x + y within the domain x² + y² ≤ 4. Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist. 1. Absolute minimum of f(x, y) isarrow_forwardSuppose that one factory inputs its goods from two different plants, A and B, with different costs, 3 and 7 each respective. And suppose the price function in the market is decided as p(x, y) = 100 - x - y where I and y are the demand functions and 0 < x,y. Then as x = y = the factory can attain the maximum profit,arrow_forward0|0|0|0 - Consider the time series X₁ and Y₁ = (I – B)² (I – B³)Xt. What transformations were performed on Xt to obtain Yt? seasonal difference of order 2 simple difference of order 5 seasonal difference of order 1 seasonal difference of order 5 simple difference of order 2arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill  Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning





