Discrete Mathematics with Graph Theory (Classic Version) (3rd Edition) (Pearson Modern Classics for Advanced Mathematics Series)
3rd Edition
ISBN: 9780134689555
Author: Edgar Goodaire, Michael Parmenter
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 12, Problem 12RE
To determine
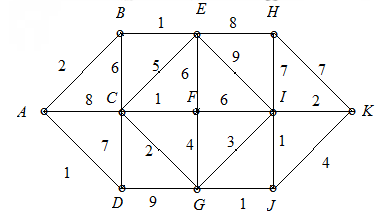
A minimum spanning tree of the weighted graph shown by using Prim’s algorithm. Also find the weight of a minimum spanning tree.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Students were asked to simplify the expression (secØ - cosØ)/secØ Two students' work is given.Student A: step 1 secØ/secØ - cosØ/secØstep 2 cosØ/1 - (1/cosØ)step 3 1 - cos^2Østep 4 sin^2ØStudent B: step 1 (1/cosØ)-cosØ)/secØstep 2 (1 - cos^2Ø/cosØ)/secØstep 3 sin^2Ø/cos^2Østep 4 tan^2ØPart A: Which student simplified the expression incorrectly? Explain the errors that were made or the formulas that were misused.Part B: Complete the student's solution correctly, beginning with the location of the error.
Although 330° is a special angle on the unit circle, Amar wanted to determine its coordinates using the sum and difference formulas.Part A: Determine cos 330° using the cosine sum identity. Be sure to include all necessary work.Part B: Determine sin 330° using the sine difference identity. Be sure to include all necessary work.
A public health researcher is studying the impacts of nudge marketing techniques on shoppers vegetables
Chapter 12 Solutions
Discrete Mathematics with Graph Theory (Classic Version) (3rd Edition) (Pearson Modern Classics for Advanced Mathematics Series)
Ch. 12.1 - Prob. 1TFQCh. 12.1 - Prob. 2TFQCh. 12.1 - Prob. 3TFQCh. 12.1 - Prob. 4TFQCh. 12.1 - Prob. 5TFQCh. 12.1 - Prob. 6TFQCh. 12.1 - Prob. 7TFQCh. 12.1 - Prob. 8TFQCh. 12.1 - Prob. 9TFQCh. 12.1 - Prob. 10TFQ
Ch. 12.1 - Prob. 1ECh. 12.1 - Prob. 2ECh. 12.1 - Prob. 3ECh. 12.1 - Prob. 4ECh. 12.1 - Prob. 5ECh. 12.1 - Prob. 6ECh. 12.1 - Prob. 7ECh. 12.1 - Prob. 8ECh. 12.1 - 9. The vertices in the graph represent town; the...Ch. 12.1 - Prob. 11ECh. 12.1 - 12. [BB] suppose and are two paths from a vertex...Ch. 12.1 - Prob. 13ECh. 12.1 - Prob. 14ECh. 12.1 - Prob. 15ECh. 12.1 - Prob. 16ECh. 12.1 - 17. [BB] Recall that a graph is acyclic if it has...Ch. 12.1 - Prob. 18ECh. 12.1 - Prob. 19ECh. 12.1 - Prob. 20ECh. 12.1 - Prob. 21ECh. 12.1 - Prob. 22ECh. 12.1 - The answers to exercises marked [BB] can be found...Ch. 12.1 - Prob. 24ECh. 12.1 - Prob. 25ECh. 12.1 - A forest is a graph every component of which is a...Ch. 12.1 - Prob. 27ECh. 12.2 - Prob. 1TFQCh. 12.2 - Prob. 2TFQCh. 12.2 - Prob. 3TFQCh. 12.2 - Prob. 4TFQCh. 12.2 - Prob. 5TFQCh. 12.2 - Prob. 6TFQCh. 12.2 - Prob. 7TFQCh. 12.2 - Prob. 8TFQCh. 12.2 - Prob. 9TFQCh. 12.2 - Prob. 1ECh. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Prob. 6ECh. 12.2 - Prob. 7ECh. 12.2 - Prob. 8ECh. 12.2 - Prob. 9ECh. 12.2 - Prob. 10ECh. 12.2 - Prob. 11ECh. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.3 - If Kruskal’s algorithm is applied to after one...Ch. 12.3 - 2. If Kruskal’s algorithm is applied to we might...Ch. 12.3 - 3. If Kruskal’s algorithm is applied to we might...Ch. 12.3 - If Prim’s algorithm is applied to after one...Ch. 12.3 - If Prims algorithm is applied to we might end up...Ch. 12.3 - If Prims algorithm is applied to we might end up...Ch. 12.3 - Prob. 7TFQCh. 12.3 - Prob. 8TFQCh. 12.3 - Prob. 9TFQCh. 12.3 - Prob. 10TFQCh. 12.3 - Prob. 1ECh. 12.3 - Prob. 2ECh. 12.3 - Prob. 3ECh. 12.3 - Prob. 4ECh. 12.3 - The answers to exercises marked [BB] can be found...Ch. 12.3 - Prob. 6ECh. 12.3 - Prob. 7ECh. 12.3 - Prob. 8ECh. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - In our discussion of the complexity of Kruskals...Ch. 12.3 - Prob. 13ECh. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - Prob. 17ECh. 12.3 - Prob. 18ECh. 12.4 - The digraph pictured by is a cyclic.Ch. 12.4 - Prob. 2TFQCh. 12.4 - Prob. 3TFQCh. 12.4 - Prob. 4TFQCh. 12.4 - Prob. 5TFQCh. 12.4 - Prob. 6TFQCh. 12.4 - Prob. 7TFQCh. 12.4 - Prob. 8TFQCh. 12.4 - Prob. 9TFQCh. 12.4 - Prob. 10TFQCh. 12.4 - Prob. 1ECh. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Prob. 4ECh. 12.4 - 5. The algorithm described in the proof of...Ch. 12.4 - How many shortest path algorithms can you name?...Ch. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 10ECh. 12.4 - Prob. 11ECh. 12.4 - Prob. 12ECh. 12.4 - [BB] Explain how Bellmans algorithm can be...Ch. 12.4 - Prob. 14ECh. 12.5 - Prob. 1TFQCh. 12.5 - Depth-first search has assigned labels 1 and 2 as...Ch. 12.5 - Depth-first search has assigned labels 1 and 2 as...Ch. 12.5 - Prob. 4TFQCh. 12.5 - Prob. 5TFQCh. 12.5 - Prob. 6TFQCh. 12.5 - Prob. 7TFQCh. 12.5 - Prob. 8TFQCh. 12.5 - 9. Breadth-first search (see exercise 10) has...Ch. 12.5 - Prob. 10TFQCh. 12.5 - Prob. 1ECh. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - 4. (a) [BB] Let v be a vertex in a graph G that is...Ch. 12.5 - Prob. 5ECh. 12.5 - Prob. 6ECh. 12.5 - Prob. 7ECh. 12.5 - Prob. 8ECh. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - [BB; (a)] Apply a breath-first search to each of...Ch. 12.5 - Prob. 12ECh. 12.5 - Prob. 13ECh. 12.5 - Prob. 14ECh. 12.6 - Prob. 1TFQCh. 12.6 - Prob. 2TFQCh. 12.6 - Prob. 3TFQCh. 12.6 - Prob. 4TFQCh. 12.6 - Prob. 5TFQCh. 12.6 - Prob. 6TFQCh. 12.6 - Prob. 7TFQCh. 12.6 - Prob. 8TFQCh. 12.6 - Prob. 9TFQCh. 12.6 - Prob. 10TFQCh. 12.6 - Prob. 1ECh. 12.6 - Prob. 2ECh. 12.6 - Prob. 3ECh. 12.6 - Prob. 4ECh. 12.6 - Prob. 5ECh. 12.6 - Prob. 6ECh. 12.6 - Prob. 7ECh. 12.6 - Prob. 8ECh. 12.6 - Prob. 9ECh. 12.6 - Prob. 10ECh. 12.6 - Prob. 11ECh. 12.6 - Prob. 12ECh. 12.6 - Prob. 13ECh. 12.6 - Prob. 14ECh. 12.6 - Prob. 15ECh. 12 - Prob. 1RECh. 12 - Prob. 2RECh. 12 - Prob. 3RECh. 12 - Prob. 4RECh. 12 - 5. (a) Let G be a graph with the property that...Ch. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Prob. 15RECh. 12 - Prob. 16RECh. 12 - Prob. 17RECh. 12 - Prob. 18RECh. 12 - In each of the following graphs, a depth-first...Ch. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 4. Let A {w, e, s, t, f, i, e, l, d, s, t, a, t, e}. (a) How many different words (they do not have to make sense) can you spell with the letters in A? (b) Is your answer from above the same as the cardinality of the powerset of A, i.e. of P(A)? (c) What is |A|?arrow_forwardwhat can the answer be pls helparrow_forward5. How many numbers can you make out of the digits 1, 2, 3, 4, 6 if the rule is that every digit has to be larger than the digit preceding it? For example 124 is ok, 122 is not ok. Every digit can be used only once, but you do not have to use every digit. A tree might help.arrow_forward
- The director of admissions at Kinzua University in Nova Scotia estimated the distribution of student admissions for the fall semester on the basis of past experience. Admissions Probability 1,100 0.5 1,400 0.4 1,300 0.1 Click here for the Excel Data File Required: What is the expected number of admissions for the fall semester? Compute the variance and the standard deviation of the number of admissions. Note: Round your standard deviation to 2 decimal places.arrow_forwardDo number 3 plsarrow_forward10 plsarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License