Discrete Mathematics with Graph Theory (Classic Version) (3rd Edition) (Pearson Modern Classics for Advanced Mathematics Series)
3rd Edition
ISBN: 9780134689555
Author: Edgar Goodaire, Michael Parmenter
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
Chapter 12.2, Problem 2E
(a)
To determine
Three spanning trees representing two isomorphism classes of graph using the graph shown below and also find the total number of spanning trees.
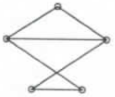
(b)
To determine
Three spanning trees representing two isomorphism classes of graph shown below and also find the total number of spanning trees.
(c)
To determine
Three spanning trees representing two isomorphism classes of graph shown below and also find the total number of spanning trees.
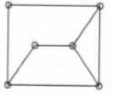
(d)
To determine
Three spanning trees representing two isomorphism classes of graph shown below and also find the total number of spanning trees.
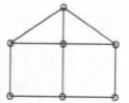
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Which angles are complementary to each other? Select all that apply.
3
2
4
in
5
1
Z1 and 23
Z1 and 25
22 and 23
Z2 and 25
Submit
Which angles are adjacent to each other? Select all that apply.
3
2
4
67
5 8
11
10
12
12
9
27 and 28
Z9 and 12
Z3 and 24
Z10 and
Z11
If the arc length of NMP is 11π, what is the length
of MNP expressed in terms of πT?
M
N
5 44%
○ A. 54π
OB. 108π
P
О с.
103
18
O D.
108
Chapter 12 Solutions
Discrete Mathematics with Graph Theory (Classic Version) (3rd Edition) (Pearson Modern Classics for Advanced Mathematics Series)
Ch. 12.1 - Prob. 1TFQCh. 12.1 - Prob. 2TFQCh. 12.1 - Prob. 3TFQCh. 12.1 - Prob. 4TFQCh. 12.1 - Prob. 5TFQCh. 12.1 - Prob. 6TFQCh. 12.1 - Prob. 7TFQCh. 12.1 - Prob. 8TFQCh. 12.1 - Prob. 9TFQCh. 12.1 - Prob. 10TFQ
Ch. 12.1 - Prob. 1ECh. 12.1 - Prob. 2ECh. 12.1 - Prob. 3ECh. 12.1 - Prob. 4ECh. 12.1 - Prob. 5ECh. 12.1 - Prob. 6ECh. 12.1 - Prob. 7ECh. 12.1 - Prob. 8ECh. 12.1 - 9. The vertices in the graph represent town; the...Ch. 12.1 - Prob. 11ECh. 12.1 - 12. [BB] suppose and are two paths from a vertex...Ch. 12.1 - Prob. 13ECh. 12.1 - Prob. 14ECh. 12.1 - Prob. 15ECh. 12.1 - Prob. 16ECh. 12.1 - 17. [BB] Recall that a graph is acyclic if it has...Ch. 12.1 - Prob. 18ECh. 12.1 - Prob. 19ECh. 12.1 - Prob. 20ECh. 12.1 - Prob. 21ECh. 12.1 - Prob. 22ECh. 12.1 - The answers to exercises marked [BB] can be found...Ch. 12.1 - Prob. 24ECh. 12.1 - Prob. 25ECh. 12.1 - A forest is a graph every component of which is a...Ch. 12.1 - Prob. 27ECh. 12.2 - Prob. 1TFQCh. 12.2 - Prob. 2TFQCh. 12.2 - Prob. 3TFQCh. 12.2 - Prob. 4TFQCh. 12.2 - Prob. 5TFQCh. 12.2 - Prob. 6TFQCh. 12.2 - Prob. 7TFQCh. 12.2 - Prob. 8TFQCh. 12.2 - Prob. 9TFQCh. 12.2 - Prob. 1ECh. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Prob. 6ECh. 12.2 - Prob. 7ECh. 12.2 - Prob. 8ECh. 12.2 - Prob. 9ECh. 12.2 - Prob. 10ECh. 12.2 - Prob. 11ECh. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.3 - If Kruskal’s algorithm is applied to after one...Ch. 12.3 - 2. If Kruskal’s algorithm is applied to we might...Ch. 12.3 - 3. If Kruskal’s algorithm is applied to we might...Ch. 12.3 - If Prim’s algorithm is applied to after one...Ch. 12.3 - If Prims algorithm is applied to we might end up...Ch. 12.3 - If Prims algorithm is applied to we might end up...Ch. 12.3 - Prob. 7TFQCh. 12.3 - Prob. 8TFQCh. 12.3 - Prob. 9TFQCh. 12.3 - Prob. 10TFQCh. 12.3 - Prob. 1ECh. 12.3 - Prob. 2ECh. 12.3 - Prob. 3ECh. 12.3 - Prob. 4ECh. 12.3 - The answers to exercises marked [BB] can be found...Ch. 12.3 - Prob. 6ECh. 12.3 - Prob. 7ECh. 12.3 - Prob. 8ECh. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - In our discussion of the complexity of Kruskals...Ch. 12.3 - Prob. 13ECh. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - Prob. 17ECh. 12.3 - Prob. 18ECh. 12.4 - The digraph pictured by is a cyclic.Ch. 12.4 - Prob. 2TFQCh. 12.4 - Prob. 3TFQCh. 12.4 - Prob. 4TFQCh. 12.4 - Prob. 5TFQCh. 12.4 - Prob. 6TFQCh. 12.4 - Prob. 7TFQCh. 12.4 - Prob. 8TFQCh. 12.4 - Prob. 9TFQCh. 12.4 - Prob. 10TFQCh. 12.4 - Prob. 1ECh. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Prob. 4ECh. 12.4 - 5. The algorithm described in the proof of...Ch. 12.4 - How many shortest path algorithms can you name?...Ch. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 10ECh. 12.4 - Prob. 11ECh. 12.4 - Prob. 12ECh. 12.4 - [BB] Explain how Bellmans algorithm can be...Ch. 12.4 - Prob. 14ECh. 12.5 - Prob. 1TFQCh. 12.5 - Depth-first search has assigned labels 1 and 2 as...Ch. 12.5 - Depth-first search has assigned labels 1 and 2 as...Ch. 12.5 - Prob. 4TFQCh. 12.5 - Prob. 5TFQCh. 12.5 - Prob. 6TFQCh. 12.5 - Prob. 7TFQCh. 12.5 - Prob. 8TFQCh. 12.5 - 9. Breadth-first search (see exercise 10) has...Ch. 12.5 - Prob. 10TFQCh. 12.5 - Prob. 1ECh. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - 4. (a) [BB] Let v be a vertex in a graph G that is...Ch. 12.5 - Prob. 5ECh. 12.5 - Prob. 6ECh. 12.5 - Prob. 7ECh. 12.5 - Prob. 8ECh. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - [BB; (a)] Apply a breath-first search to each of...Ch. 12.5 - Prob. 12ECh. 12.5 - Prob. 13ECh. 12.5 - Prob. 14ECh. 12.6 - Prob. 1TFQCh. 12.6 - Prob. 2TFQCh. 12.6 - Prob. 3TFQCh. 12.6 - Prob. 4TFQCh. 12.6 - Prob. 5TFQCh. 12.6 - Prob. 6TFQCh. 12.6 - Prob. 7TFQCh. 12.6 - Prob. 8TFQCh. 12.6 - Prob. 9TFQCh. 12.6 - Prob. 10TFQCh. 12.6 - Prob. 1ECh. 12.6 - Prob. 2ECh. 12.6 - Prob. 3ECh. 12.6 - Prob. 4ECh. 12.6 - Prob. 5ECh. 12.6 - Prob. 6ECh. 12.6 - Prob. 7ECh. 12.6 - Prob. 8ECh. 12.6 - Prob. 9ECh. 12.6 - Prob. 10ECh. 12.6 - Prob. 11ECh. 12.6 - Prob. 12ECh. 12.6 - Prob. 13ECh. 12.6 - Prob. 14ECh. 12.6 - Prob. 15ECh. 12 - Prob. 1RECh. 12 - Prob. 2RECh. 12 - Prob. 3RECh. 12 - Prob. 4RECh. 12 - 5. (a) Let G be a graph with the property that...Ch. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Prob. 15RECh. 12 - Prob. 16RECh. 12 - Prob. 17RECh. 12 - Prob. 18RECh. 12 - In each of the following graphs, a depth-first...Ch. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RE
Knowledge Booster
Similar questions
- Using Karnaugh maps and Gray coding, reduce the following circuit represented as a table and write the final circuit in simplest form (first in terms of number of gates then in terms of fan-in of those gates). HINT: Pay closeattention to both the 1’s and the 0’s of the function.arrow_forwardRecall the RSA encryption/decryption system. The following questions are based on RSA. Suppose n (=15) is the product of the two prime numbers 3 and 5.1. Find an encryption key e for for the pair (e, n)2. Find a decryption key d for for the pair (d, n)3. Given the plaintext message x = 3, find the ciphertext y = x^(e) (where x^e is the message x encoded with encryption key e)4. Given the ciphertext message y (which you found in previous part), Show that the original message x = 3 can be recovered using (d, n)arrow_forwardTheorem 1: A number n ∈ N is divisible by 3 if and only if when n is writtenin base 10 the sum of its digits is divisible by 3. As an example, 132 is divisible by 3 and 1 + 3 + 2 is divisible by 3.1. Prove Theorem 1 2. Using Theorem 1 construct an NFA over the alphabet Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}which recognizes the language {w ∈ Σ^(∗)| w = 3k, k ∈ N}.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education