Chapter 12, Problem 12P

Review. While Lost-a-Lot ponders his next move in the situation described in Problem 11 and illustrated in Figure P12.11, the enemy attacks! An incoming projectile breaks off the stone ledge so that the end of the drawbridge can be lowered past the wall where it usually rests. In addition, a fragment of the projectile bounces up and cuts the drawbridge cable! The hinge between the castle wall and the bridge is frictionless, and the bridge swings down freely until it is vertical and smacks into the vertical castle wall below the castle entrance. (a) How long does Lost-a-Lot stay in contact with the bridge while it swings downward? 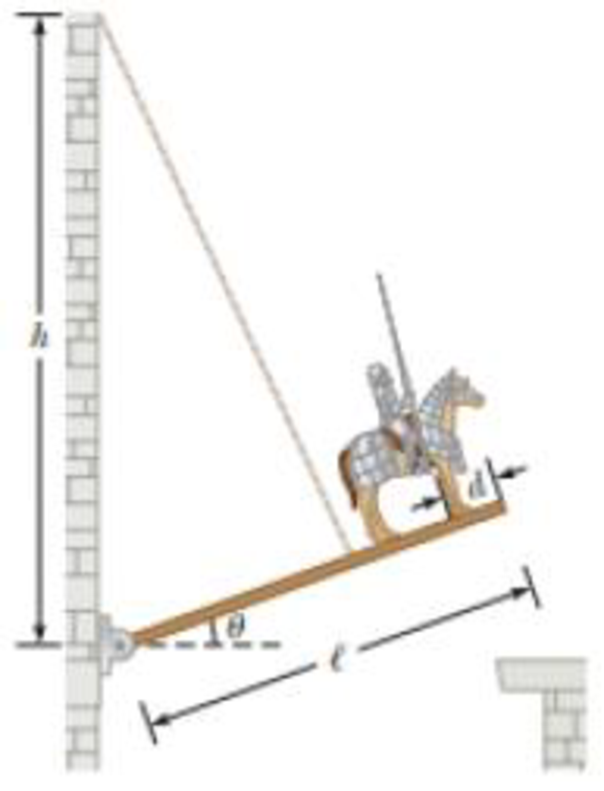(b) Find the angular acceleration of the bridge just as it starts to move. (c) Find the angular speed of the bridge when it strikes the wall below the hinge. Find the force exerted by the hinge on the bridge (d) immediately after the cable breaks and (e) immediately before it strikes the castle wall.

To determine

The time that Lost a Lot stay in contact with the bridge while it swings downward.

Answer to Problem 12P

The time that Lost a Lot stay in contact with the bridge while it swings downward is $0\text{s}$.

Explanation of Solution

Given info: The length of the uniform bridge is $8.00\text{m}$, the mass of the bridge is $2000\text{kg}$, the height of the castle wall is $12.0\text{m}$ and the angle made by the bridge from of horizontal is $20.0°$.

There is no time interval as the Lost a Lot stay in contact with the bridge while it swings downward because the horse feet loose contact with the down bridge as soon as it begins to move because the vertical acceleration act on the feet is greater than the acceleration due to gravity due to that the horse is in the air and moves upward with a vertical component of acceleration.

Conclusion:

Therefore, the time that Lost a Lot stay in contact with the bridge while it swings downward is $0\text{s}$.

To determine

The angular acceleration of the bridge just as it starts to move.

Answer to Problem 12P

The angular acceleration of the bridge just as it starts to move is $1.73{\text{rad}/\text{s}}^2$.

Explanation of Solution

Given info: The length of the uniform bridge is $8.00\text{m}$, the mass of the bridge is $2000\text{kg}$, the height of the castle wall is $12.0\text{m}$ and the angle made by the bridge from of horizontal is $20.0°$.

The mass moment of inertial along the centroid is,

$I=\frac{1}{3}m{l}^2$

The total moment along the centroid is,

${\displaystyle \sum M}=mg\left(\frac{l}{2}\right)\cos \theta$

Here,

$I$ is the mass moment o0f inertia along the centroid.

$m$ is the mass of the bridge.

$l$ is the length of the bridge.

$g$ is the acceleration due to gravity.

$\theta$ is the angle made by the bridge from of horizontal.

Total moment along the centroid is,

${\displaystyle \sum M}=I\alpha$ (1)

Here,

$M$ is the moment along centroid of bridge.

$\alpha$ is the angular acceleration.

Substitute $mg\left(\frac{l}{2}\right)\cos \theta$ for ${\displaystyle \sum M}$ and $\frac{1}{3}m{l}^2$ for $I$ in equation (1).

$\begin{array}{c}mg\left(\frac{l}{2}\right)\cos \theta =\frac{1}{3}m{l}^2\alpha \\ \alpha =\frac{3g\cos \theta }{2l}\end{array}$ (2)

Substitute $9.81{\text{m}/\text{s}}^2$ for $g$, $20.0°$ for $\theta$ and $8\text{m}$ for $l$ in equation (2)

$\begin{array}{c}\alpha =\frac{3\left(9.81{\text{m}/\text{s}}^2\right)\cos \left(20.0°\right)}{2\left(8.00\text{m}\right)}\\ =1.73{\text{rad}/\text{s}}^2\end{array}$

Conclusion:

Therefore, the angular acceleration of the bridge just as it starts to move is $1.73{\text{rad}/\text{s}}^2$.

To determine

The angular speed of the bridge when it strikes the wall below the hinge.

Answer to Problem 12P

The angular speed of the bridge when it strikes the wall below the hinge is $2.22\text{rad}/\text{s}$.

Explanation of Solution

Given info: The length of the uniform bridge is $8.00\text{m}$, the mass of the bridge is $2000\text{kg}$, the height of the castle wall is $12.0\text{m}$ and the angle made by the bridge from of horizontal is $20.0°$.

The total height of the wall from the point of hinge is,

$\begin{array}{c}h=\frac{l}{2}+\frac{l}{2}\sin \theta \\ =\frac{l}{2}\left(1+\sin \theta \right)\end{array}$

Here,

$h$ is the height of the castle wall.

From the conservation of energy, the total potential energy will be equal to the rotational energy is,

$mgh=\frac{1}{2}I{\omega }^2$ (2)

Here,

$\omega$ is the angular speed.

Substitute $\frac{l}{2}\left(1+\sin \theta \right)$ for $h$ and $\frac{1}{3}m{l}^2$ for $I$ in equation (2) to find $\omega$.

$\begin{array}{c}mg\frac{l}{2}\left(1+\sin \theta \right)=\frac{1}{2}\left(\frac{1}{3}m{l}^2\right){\omega }^2\\ \omega =\sqrt{\frac{3g\left(1+\sin \theta \right)}{l}}\end{array}$ (3)

Substitute $9.81{\text{m}/\text{s}}^2$ for $g$, $20.0°$ for $\theta$ and $8\text{m}$ for $l$ in equation (3).

$\begin{array}{c}\omega =\sqrt{\frac{3\left(9.81{\text{m}/\text{s}}^2\right)\left(1+\sin \left(20.0°\right)\right)}{8\text{m}}}\\ =2.22\text{rad}/\text{s}\end{array}$

Conclusion:

Therefore, the angular speed of the bridge when it strikes the wall below the hinge is $2.22\text{rad}/\text{s}$.

To determine

The force exerted by the hinge on the bridge immediately after the cable breaks.

Answer to Problem 12P

The force exerted by the hinge on the bridge immediately after the cable breaks is $\left(4.72\widehat{\text{i}}+6.62\widehat{\text{j}}\right)\text{kN}$.

Explanation of Solution

Given info: The length of the uniform bridge is $8.00\text{m}$, the mass of the bridge is $2000\text{kg}$, the height of the castle wall is $12.0\text{m}$ and the angle made by the bridge from of horizontal is $20.0°$.

From Figure (1), the tangential acceleration is,

$a_{\text{t}}=\frac{l}{2}\alpha$

Here,

$a_{\text{t}}$ is the tangential acceleration.

Substitute $8.00\text{m}$ for $l$ and $1.73{\text{rad}/\text{s}}^2$ for $\alpha$ in above equation to find $a_{\text{t}}$.

$\begin{array}{c}{a}_{\text{t}}=\frac{8.00\text{m}}{2}\left(1.73{\text{rad}/\text{s}}^2\right)\\ =6.92{\text{m}/\text{s}}^2\end{array}$

Thus, the tangential acceleration is $6.92{\text{m}/\text{s}}^2$.

The acceleration along the horizontal is,

$a_{\text{x}}=a_{\text{t}}\sin \theta$

Here,

$a_{\text{x}}$ is the acceleration along the horizontal.

The acceleration along the vertical is,

$a_{\text{y}}=\left(g-a_{\text{t}}\cos \theta \right)$

Here,

$a_{\text{y}}$ is the acceleration along the vertical

Force along the horizontal direction is,

$F_{\text{x}}={\mathrm{ma}}_{\text{x}}$ (4)

Here,

$F_{\text{x}}$ is the force along the horizontal.

Substitute $a_{\text{t}}\sin 20°$ for $a_{\text{x}}$ in equation (4).

$F_{\text{x}}=\mathrm{m}{a}_{\text{t}}\sin \theta$ (5)

Substitute $2000\text{kg}$ for $m$, $20.0°$ for $\theta$ and $6.92{\text{m}/\text{s}}^2$ for $a_{\text{t}}$ in equation (5) to find $F_{\text{x}}$.

$\begin{array}{c}{F}_{\text{x}}=\left(2000\text{kg}\right)\left(6.92{\text{m}/\text{s}}^2\right)\sin \left(20°\right)\\ =4.72\times {10}^3\text{N}\left(\frac{{10}^{-3}\text{kN}}{1\text{N}}\right)\\ =4.72\text{kN}\end{array}$

Thus, the force along the horizontal is $4.72\text{kN}$.

Force along the vertical is,

$F_{\text{y}}=m{a}_{\text{y}}$ (6)

Here,

$F_{\text{y}}$ is the force along the vertical.

Substitute $\left(g-a_{\text{t}}\cos \theta \right)$ foe $a_{\text{y}}$ in equation (6).

$F_{\text{y}}=m\left(g-a_{\text{t}}\cos \theta \right)$ (7)

Substitute $2000\text{kg}$ for $m$, $20.0°$ for $\theta$, $9.81{\text{m}/\text{s}}^2$ for $g$ and $6.92{\text{m}/\text{s}}^2$ for $a_{\text{t}}$ in equation (7) to find $F_{\text{y}}$.

$\begin{array}{c}{F}_{\text{y}}=\left(2000\text{kg}\right)\left(9.81{\text{m}/\text{s}}^2-\left(6.92{\text{m}/\text{s}}^2\right)\cos 20.0°\right)\\ =6.62\text{N}\left(\frac{{10}^{-3}\text{kN}}{1\text{N}}\right)\\ =6.62\text{kN}\end{array}$

Thus, the vertical force is $6.62\text{kN}$.

The force exerted by the hinge on the bridge is,

$F=F_{\text{x}}+F_{\text{y}}$ (8)

Here,

$F$ is the force exerted by the hinge on the bridge.

Substitute $6.62\text{kN}$ for $F_{\text{y}}$ and $4.72\text{kN}$ for $F_{\text{x}}$ in equation (8) to find $F$.

$F=\left(4.72\widehat{\text{i}}+6.62\widehat{\text{j}}\right)\text{kN}$

Conclusion:

Therefore, the force exerted by the hinge on the bridge immediately after the cable breaks is $\left(4.72\widehat{\text{i}}+6.62\widehat{\text{j}}\right)\text{kN}$.

To determine

The force exerted by the hinge on the bridge immediately before strikes the cable wall.

Answer to Problem 12P

The force exerted by the hinge on the bridge immediately before strikes the cable wall is $59.1\text{kN}$.

Explanation of Solution

Given info: The length of the uniform bridge is $8.00\text{m}$, the mass of the bridge is $2000\text{kg}$, the height of the castle wall is $12.0\text{m}$ and the angle made by the bridge from of horizontal is $20.0°$.

The acceleration along the vertical is,

$a_{\text{y}}={\omega }^2\frac{l}{2}$

From Newton’s second law, the total force along the vertical is,

$\begin{array}{c}{\displaystyle \sum F_{\text{y}}}=m{a}_{\text{y}}\\ F_{\text{y}}-mg=m{a}_{\text{y}}\\ F_{\text{y}}=m\left(g+a_{\text{y}}\right)\end{array}$ (9)

Substitute ${\omega }^2\frac{l}{2}$ for $a_{\text{y}}$ in equation (9) to find $F_{\text{y}}$.

$F_{\text{y}}=m\left(g+{\omega }^2\frac{l}{2}\right)$ (10)

Substitute $2000\text{kg}$ for $m$, $2.22\text{rad}/\text{s}$ for $\omega$, $9.81{\text{m}/\text{s}}^2$ for $g$ and $8.00\text{m}$ for $l$ in equation (10) to find $F_{\text{y}}$.

$\begin{array}{c}{F}_{\text{y}}=\left(2000\text{kg}\right)\left(9.81{\text{m}/\text{s}}^2+{\left(2.22\text{rad}/\text{s}\right)}^2\frac{8.00\text{m}}{2}\right)\\ =59.1\text{N}\left(\frac{{10}^{-3}\text{kN}}{1\text{N}}\right)\\ =59.1\text{kN}\end{array}$

Conclusion:

Therefore, the force exerted by the hinge on the bridge immediately before strikes the cable wall is $59.1\text{kN}$.