
Concept explainers
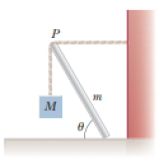
A uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end (point P) produces a 90° bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (Fig. P12.35). Let μs represent the coefficient of static friction between beam and floor. Assume μs is less than the cotangent of θ. (a) Find an expression for the maximum mass M that can be suspended from the top before the beam slips. Determine (b) the magnitude of the reaction force at the floor and (c) the magnitude of the force exerted by the beam on the rope at P in terms of m, M, and μs.
Figure P12.35
(a)
The expression for the maximum mass that can be suspended from the top surface before the beam starts slip.
Answer to Problem 12.51AP
The expression for the maximum mass that can be suspended from the top surface before the beam starts slip is
Explanation of Solution
The mass of the beam is
The following figure shows the force diagram of the beam.

Figure-(I)
Formula to calculate the frictional force acting on the base of the beam is,
Here,
Formula to calculate the net torque about the point
Here,
Rearrange the above equation to find
Formula to calculate the net vertical forces is,
Rearrange the above equation to find
Formula to calculate the net horizontal force is,
Substitute
Further simplify the above equation to find
Conclusion:
Therefore, the expression for the maximum mass that can be suspended from the top surface before the beam starts slip is
(b)
The magnitude of the reaction force at the floor.
Answer to Problem 12.51AP
The magnitude of the reaction force at the floor is
Explanation of Solution
The mass of the beam is
Formula to calculate the net reaction force acting in the floor is,
Here,
Substitute
Conclusion:
Therefore, the magnitude of the reaction force at the floor is
(c)
The magnitude of the force exerted by the beam in the rope at
Answer to Problem 12.51AP
The magnitude of the force exerted by the beam in the rope at
Explanation of Solution
The mass of the beam is
Since the coefficient of static friction of the floor is less than cotangent of the angle
Substitute
Formula to calculate the magnitude of the net force exerted by the beam in the rope at point
Here,
Substitute
Substitute
Conclusion:
Therefore, the magnitude of the force exerted by the beam in the rope at
Want to see more full solutions like this?
Chapter 12 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- please answer this asap!!!!arrow_forwardRT = 4.7E-30 18V IT = 2.3E-3A+ 12 38Ω ли 56Ω ли r5 27Ω ли r3 28Ω r4 > 75Ω r6 600 0.343V 75.8A Now figure out how much current in going through the r4 resistor. |4 = unit And then use that current to find the voltage drop across the r resistor. V4 = unitarrow_forward7 Find the volume inside the cone z² = x²+y², above the (x, y) plane, and between the spheres x²+y²+z² = 1 and x² + y²+z² = 4. Hint: use spherical polar coordinates.arrow_forward
- ганм Two long, straight wires are oriented perpendicular to the page, as shown in the figure(Figure 1). The current in one wire is I₁ = 3.0 A, pointing into the page, and the current in the other wire is 12 4.0 A, pointing out of the page. = Find the magnitude and direction of the net magnetic field at point P. Express your answer using two significant figures. VO ΜΕ ΑΣΦ ? Figure P 5.0 cm 5.0 cm ₁ = 3.0 A 12 = 4.0 A B: μΤ You have already submitted this answer. Enter a new answer. No credit lost. Try again. Submit Previous Answers Request Answer 1 of 1 Part B X Express your answer using two significant figures. ΜΕ ΑΣΦ 0 = 0 ? below the dashed line to the right P You have already submitted this answer. Enter a new answer. No credit lost. Try again.arrow_forwardAn infinitely long conducting cylindrical rod with a positive charge λ per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of −2λ and radius r1, as shown in the figure. What is σinner, the surface charge density (charge per unit area) on the inner surface of the conducting shell? What is σouter, the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by −2λ.)arrow_forwardA small conducting spherical shell with inner radius aa and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d (Figure 1). The inner shell has total charge +2q, and the outer shell has charge −2q. What's the total charge on the inner surface of the small shell? What's the total charge on the outer surface of the small shell? What's the total charge on the inner surface of the large shell? What's the total charge on the outer surface of the large shell?arrow_forward
- A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius cc and outer radius d (Figure 1). The inner shell has total charge +2q, and the outer shell has charge −2q. What is the direction of the electric field for b<r<c? Calculate the magnitude of the electric field for c<r<d. Calculate the magnitude of the electric field for r>d.arrow_forwardTICE D Conservation of Momentum 1. A 63.0 kg astronaut is on a spacewalk when the tether line to the shuttle breaks. The astronaut is able to throw a spare 10.0 kg oxygen tank in a direction away from the shuttle with a speed of 12.0 m/s, propelling the astronaut back to the shuttle. Assuming that the astronaut starts from rest with respect to the shuttle, find the astronaut's final speed with respect to the shuttle after the tank is thrown. 2. An 85.0 kg fisherman jumps from a dock into a 135.0 kg rowboat at rest on the west side of the dock. If the velocity of the fisherman is 4.30 m/s to the west as he leaves the dock, what is the final velocity of the fisher- man and the boat? 3. Each croquet ball in a set has a mass of 0.50 kg. The green ball, traveling at 12.0 m/s, strikes the blue ball, which is at rest. Assuming that the balls slide on a frictionless surface and all collisions are head-on, find the final speed of the blue ball in each of the following situations: a. The green…arrow_forwardThe 5.15 A current through a 1.50 H inductor is dissipated by a 2.15 Q resistor in a circuit like that in the figure below with the switch in position 2. 0.632/ C A L (a) 0.368/ 0+ 0 = L/R 2T 3r 4 (b) (a) What is the initial energy (in J) in the inductor? 0 t = L/R 2t (c) Эт 4t 19.89 ] (b) How long will it take (in s) the current to decline to 5.00% of its initial value? 2.09 S (c) Calculate the average power (in W) dissipated, and compare it with the initial power dissipated by the resistor. 28.5 1.96 x W X (ratio of initial power to average power)arrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





