
Concept explainers
Disk A rotates in a horizontal plane about a vertical axis at the
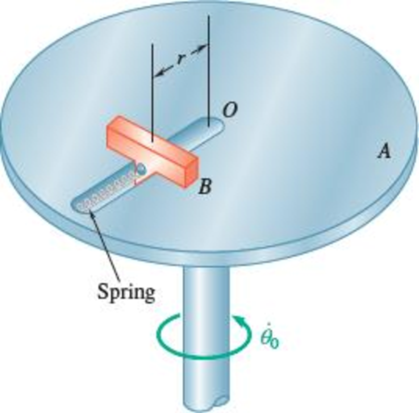
(a)
Find the position of the slider and horizontal force exerted on the slider by disk at
Answer to Problem 12.133RP
The position of the slider at
The horizontal force exerted on the slider by disk at
Explanation of Solution
Given information:
The polar coordinate
The mass
The distance
The spring constant (k) is 100 N/m.
Calculation:
Consider the Position of the slider is in point O
Find the displacement of spring when
Consider distance of the slider (r) from the point O is 500 mm.
Find the displacement of spring when
Substitute 500 mm for r.
Find the restoring force (F) of spring when
Substitute 100 N/m for k and 500 mm for
Sketch the free body diagram and kinetic diagram of forces on disk A and spring as shown in in Figure (1).
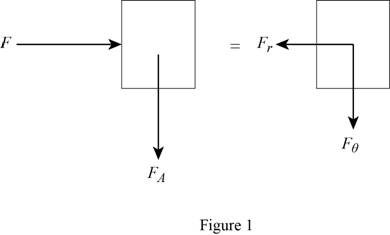
Refer Figure (1).
Write the equation of radial component of acceleration
Apply Newton’s law of equation along radial direction.
The radial force is equal to the restoring force.
Find the equation of restoring force (F).
Substitute
Substitute
Write the equation of
Integrate Equation (1) to find
Use Equation (1) to substitute for
Slider B is at initial position when
Write
Integrate Equation (4) to find
Use Equation (3) to substitute for
Find the position of the slider at
Use Equation (4) to substitute for
Thus, the position of the slider at
Refer Figure 1.
Apply Newton’s law of Equation along transverse direction.
Write the transverse component of acceleration
Here,
The transverse force is the horizontal force exerted on the slider by disk.
The disk is rotating at constant rate. Therefore, the polar coordinate of transverse acceleration,
Find the horizontal force exerted on the slider by disk at
Write the equation of transverse force
Substitute
Substitute 0 for
Substitute Equation (3) in Equation (7).
Thus, the horizontal force exerted on the slider by disk at
(b)
Find the position of the slider and horizontal force exerted on the slider by disk at
Answer to Problem 12.133RP
The position of the slider at
The horizontal force exerted on the slider by disk at
Explanation of Solution
Calculation:
Consider the Position of the slider is in point O
Find the displacement of spring when
Consider distance of the slider (r) from the point O is 500 mm.
Find the displacement of spring when
Substitute 500 mm for r.
Find the restoring force (F) of spring when
Substitute 200 N/m for k and 500 mm for
Refer Figure (1).
Write the equation of radial component of acceleration
Apply Newton’s law of equation along radial direction.
The radial force is equal to the restoring force.
Find the equation of restoring force (F).
Substitute
Substitute
Write the equation of radial velocity of the slider in terms of r.
Here,
Write equation of the rate of change of position coordinate in terms of differential equation.
Apply differentiation to Equation (8)
Rewrite Equation (10) by multiplying and dividing the right-hand side by dr.
Substitute Equation (10) to rewrite Equation (11).
Substitute Equation (8) to rewrite Equation (12).
Substitute
Apply the limits to integrate the Equation (14).
At the time of instant
Substitute Equation (8) in Equation (15).
Integrate Equation (16).
Use spherical polar coordinates and choose,
Differentiate Equation (18).
Rewrite Equation (18).
Rewrite Equation (20) for
Use Equation (20) and (21) to change the values of limit in Equation (17).
Apply the trigonometric formula of
Use Equation (23) to rewrite Equation (22).
Substitute 0.5m for
Thus, the position of the slider at
Find the radial polar coordinate of velocity using Equation (24).
Differentiate Equation (24) with respect to t.
Substitute 500 mm for
Find the horizontal force exerted on the slider by disk at
Substitute
Substitute 0.1 s for t and
Thus, the horizontal force exerted on the slider by disk at
Want to see more full solutions like this?
Chapter 12 Solutions
<LCPO> VECTOR MECH,STAT+DYNAMICS
Additional Engineering Textbook Solutions
Vector Mechanics For Engineers
BASIC BIOMECHANICS
Database Concepts (8th Edition)
Thermodynamics: An Engineering Approach
Mechanics of Materials (10th Edition)
Modern Database Management
- Determine the magnitudes of the reactions at the supports for this large plate.arrow_forwardOnly expert should solvearrow_forwardA 15 cm-OD pipe is buried with its centerline 1.25 m below the surface of the ground [k of soil is 0.35 W/(m K)]. An oil having a density of 800 kg/m³ and a specific heat of 2.1 kJ/(kg K) flows in the pipe at 5.6 L/s. Assuming a ground surface temperature of 5°C and a pipe wall temperature of 95°C, estimate the length of pipe in which the oil temperature decreases by 5.5°C. + Tε = 5ºC Z= 1.25 m D= 15 cm 7p=95°Carrow_forward
- Find the solution of the following Differential Equations 1) 4y+y=0, y(0)=2, y'(0) = 0. 2) y+y=0, y(0) = A, y'(0) = B. 3) "+2y'-8y=0, y(0)=1, y'(0)=8. 4) y"-2y-3y=0, y(0)=1, y'(0)=7. 5) y"-ky' =0, y(0)=2, y'(0) =k. 6) y+ky'-2k2y=0, y(0)=2, y'(0) = 2k. 7) y'+4y=0, y(0)=2.8 y+y-17sin(21) y(0)=-1. 9) y-y'-6y=0, y(0)=6. y'(0)=13. 10) y-y=0, 11) y"-4y+4y=0, y(0)=4, y'(0) = 0. y(0) = 2.1, y'(0)=3.9 12) y+2y+2y=0, y(0)=1, y'(0)=-3. 13) "+7y+12y=21e", y(0)=3.5, y'(0)=-10. 14) "+9y=10e", y(0)=0. y'(0) = 0. 15) y+3y+2.25y=91³ +64. y(0)=1, y'(0) = 31.5 16) "-6y+5y= 29 cos(21), y(0)=3.2, y'(0) = 6.2 17) y+2y+2y=0, y(0)=0, y'(0)=1. 18) y+2y+17y=0, y(0)=0, y'(0)=12. 19) y-4y+5y=0, y(0)-1, y'(0) 2. 20) 9y-6y+y=0. y(0)=3, y'(0)=1. 21) -2y+10y=0, y(0)=3, y'(0)=3. 22) 4y-4y+37y=0, (0) 3. y(0) 1.5 23) 4y-8y+5y=0, (0)-0, y(0) 1. 24) y+y+1.25y=0, y(0) 1. y'(0) -0.5 25) y+y=2 cos(1). y(0) 2. y'(0) = 0. 26) -4y+3y=0, (0)-3, y'(0) = 7. 27) y+2y+y=e", y(0)-0. y'(0) = 0. 29) 28) y+2y-3y-10sinh(2),…arrow_forwardNote: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting appreciate your time and effort!. Question:arrow_forward4. Block A and B are two different pieces of wood. Determine the minimum dimension for "a", if the shear stress of the wood is 50Mpa. The thickness of the wood is 30cm. 600N Aarrow_forward
- 1. Determine the reaction force at A. 60 kN 5 B 1 m 1 m- -1 m 4 3 m 30 kN marrow_forwardFind the Laplace Transform of the following functions 1) f() cos(ar) Ans. F(s)=7 2ws 2) f() sin(at) Ans. F(s)= s² + a² 3) f(r)-rcosh(at) Ans. F(s)= 2as 4)(t)=sin(at) Ans. F(s)= 2 5) f(1) = 2te' Ans. F(s)= (S-1) 5+2 6) (1) e cos() Ans. F(s) = (+2)+1 7) (1) (Acostẞr)+ Bsin(Br)) Ans. F(s)- A(s+a)+BB (s+a)+B 8) f()-(-)() Ans. F(s)= 9)(1)(1) Ans. F(s): 10) f(r),()sin() Ans. F(s): 11) 2 k 12) 0 13) 0 70 ㄷ.. a 2a 3a 4a 2 3 4 14) f(1)=1, 0<1<2 15) (1) Ksin(t) 0arrow_forward2. Determine the average normal stress developed in rod AB. The mass is 50kg and the diameter of the rod AB is 8mm. B 8 mmarrow_forward2.64 A 2.75-kN tensile load is applied to a test coupon made from 1.6-mm flat steel plate (E = 200 GPa, v = 0.30). Determine the resulting change in (a) the 50-mm gage length, (b) the width of portion AB of the test coupon, (c) the thickness of portion AB, (d) the cross-sectional area of portion AB. 2.75 kN A 12 mm 50 mm B 2.75 kNarrow_forwardProcedure:1- Cartesian system, 2(D)/(3)D,type of support2- Free body diagram3 - Find the support reactions4- If you find a negativenumber then flip the force5- Find the internal force3D\sum Fx=0\sum Fy=0\sum Fz=0\sum Mx=0\sum My=0\Sigma Mz=02D\Sigma Fx=0\Sigma Fy=0\Sigma Mz=05- Use method of sectionand cut the elementwhere you want to findthe internal force andkeep either side of thesectionarrow_forward3. The design of a pump and pipe system has been completed, except for the valves. The system is used to transpor10t water at 120°F through 2 nom sch 40 commercial steel pipe at a required flow rate of 85 gpm. Without the valves, the pump selected has the capability to overcome an additional 18 psi of pressure drop due to the valves and still provide the required flow rate. The pipe/valve joints are threaded. Determine how many 2-inch globe valves can be installed in this pump and pipe system.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





