
The gray square in Table
Apply each of the three transformations given in Table
To verify:
The three transformations of the gray square have indicated effect.
Answer to Problem 1P
Solution:
It is verified that each transformation has the indicated effect.
Explanation of Solution
Given:
The vertices of the gray square are:
Approach:
Multiplication of Matrices:
If
Transformation matrix:
Calculation:
The data matrix is given by
Plot the points on the graph and connect them by a line segment.
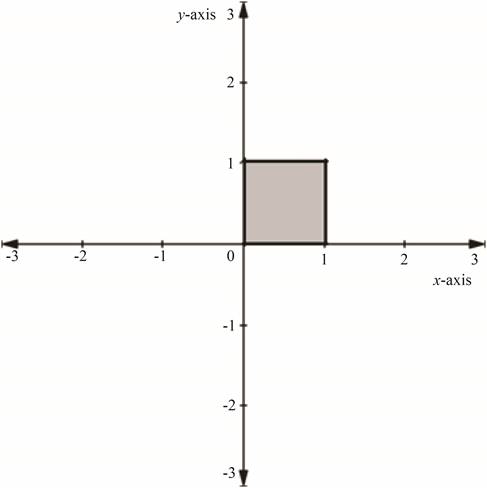
Figure
Multiply the
The following matrix is obtained
Obtain the resulting graph by plotting the points and joining them by a line.
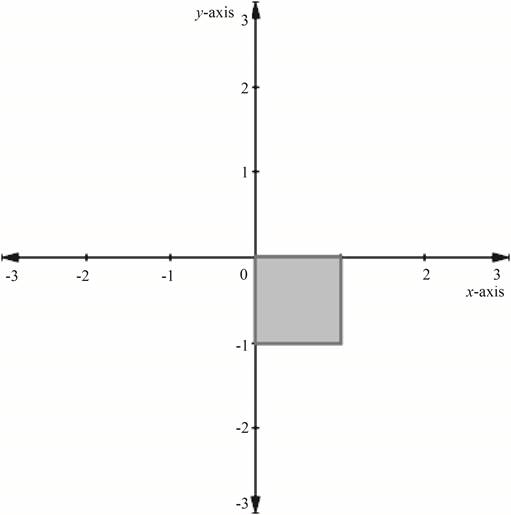
Figure
Substitute
The following matrix is obtained
Obtain the resulting graph by plotting the points and joining them by a line.
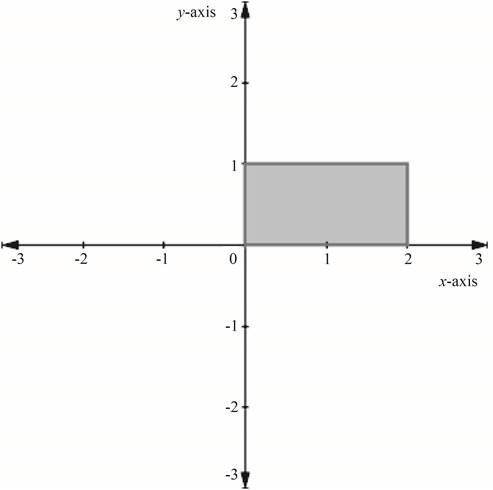
Figure
Substitute
The following matrix is obtained
Obtain the resulting graph by plotting the points and joining them by a line.
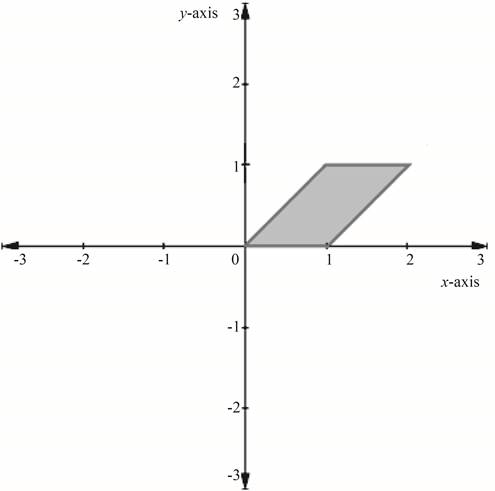
Figure
Conclusion:
Hence, it is verified that each transformation has the indicated effect.
Want to see more full solutions like this?
Chapter 11 Solutions
EBK ALGEBRA AND TRIGONOMETRY
- Practice Assignment 5.6 Rational Functions M Practice Assig Practice Assignment 5.6 Rational Functions Score: 120/150 Answered: 12/15 Question 10 A Write an equation for the function graphed below 5 + 4 1 2 H + + -7 -6 -5 -4 -3 -2 -1 2 34567 | -2 ర y = Question Help: Video Message instructor Post to forum Submit Questionarrow_forwardit's not algebra 4th gradearrow_forwardCan you tell me if I answered and showed my work correctlyarrow_forward
- Q1: A: Let M and N be two subspace of finite dimension linear space X, show that if M = N then dim M = dim N but the converse need not to be true. B: Let A and B two balanced subsets of a linear space X, show that whether An B and AUB are balanced sets or nor verly A:LeLM be a subset of a linear space X, show that M is a hyperplane of X iff there exists fe X'/[0] and a EF such that M = {x Ex/f(x) = = a}. B:Show that every two norms on finite dimension linear space are equivalent C: Let f be a linear function from a normed space X in to a normed space Y, show that continuous at x, EX iff for any sequence (x) in X converge to x, then the sequence (f(x)) converge to (f(x)) in Y.arrow_forward2/26 Delta Math | Schoology X Unit 4: Importance of Education X Speech at the United Nations b x Book Thief Part 7 Summaries x + > CA Materials pdsd.schoology.com/external_tool/3157780380/launch ☆ MC Updates Grades Members BrainPOP Canva for Education DeltaMath Discovery Education FactCite Gale In Context: High Sc. Graw McGraw Hill K-12 SSO Draw a line representing the "rise" and a line representing the "run" of the line. State the slope of the line in simplest form. Click twice to plot each segment. Click a segment to delete it. 10 9 8 5 сл y Hill Nearpod 3 2 Newsela -10 -9 -8 -7 b -5 -4-3-2 -1 1 23 4 5 b 7 89 10 Scholastic Digital Mana. World Book Online Information Grading periods MP3: 2025-01-25-2025-03- 31, MP4: 2025-04-01-2025- 06-13 ← 2 M -> C % 95 54 # m e 4 7 巴 DELL A t y & * ) 7 8 9 . i L Feb 27 12:19 US + 11arrow_forwardLet & be linear map from as Pacex into aspace and {X1, X2, – 1— x3 basis for x show that f a one-to-one isf {f(x1), f (xx); — F (Kn) } linearly independent. மம் let M be a Proper sub space of aspace X then M is ahyper space iff for any text&M X=. C) let X be a linear space and fe X1{0} Show that is bjective or not and why? ***********arrow_forward
- Q₁/(a) Let S and T be subsets of a vector space X over a field F such that SCT,show that whether (1) if S generate X then T generate X or not. (2) if T generate X then S generate X or not. (b) Let X be a vector space over a field F and A,B are subsets of X such that A is convex set and B is affine set, show that whether AnB is convex set or not, and if f be a function from X into a space Y then f(B) is an affine set or not. /(a) Let M and N be two hyperspaces of a space X write a condition to prove MUN is a hyperspace of X and condition to get that MUN is not hyperspace of X. Write with prove application n Panach theoremarrow_forwardMatch the division problem on the left with the correct quotient on the left. Note that the denominators of the reminders are omitted and replaced with R. 1) (k3-10k²+k+1) ÷ (k − 1) 2) (k4-4k-28k45k+26)+(k+7) 3) (20k+222-7k+7)+(5k-2) 4) (3+63-15k +32k-25)+(k+4) 5) (317k 13) ÷ (k+4) - 6) (k-k+8k+5)+(k+1) 7) (4-12k+6) + (k-3) 8) (3k+4k3 + 15k + 10) ÷ (3k+4) A) 3k3-6k29k - 4 B) 4k2 + 6 R 7 C)²-9k-8- R D) 4k2+6x+1+ E) 10 Elk³-5-12 R 9 F) k² - 4k R 9 R G) k3-3k2-7k+4 H) k³-k²+8 - 3 R - R 9 Rarrow_forwardAnswer choices are: 35 7 -324 4 -9 19494 5 684 3 -17 -3 20 81 15 8 -1 185193arrow_forward
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage





