Chapter 11.4, Problem 24E

Solution

a.

To find: The average rate of change of the population from $1910$ to $1950$ and $1950$ to $1990$ .

The average rate of change of the population from year $1910$ to $1950$ is $1124$ persons per year and from year $1950$ to $1990$ is $17327$ persons per year.

Given information: The table below shows the population growth of Clark County:

Year	Population
$1910$	$3321$
$1920$	$4859$
$1930$	$8532$
$1940$	$16414$
$1950$	$48289$
$1960$	$127016$
$1970$	$273288$
$1980$	$463087$
$1990$	$741368$
$2000$	$1375741$
$2010$	$1951269$
$2016$	$2155664$

Calculation:

From the table, it can be observed that the population in $1910$ is $3,321$ , in $1950$ is $48,289$ and in $1990$ is $741,368$ .

Calculate the average rate of change of the population from year $1910$ to $1950$ .

  $\begin{array}{c}\text{Average}=\frac{48289-3321}{1950-1910}\\ =\frac{44968}{40}\\ \approx 1124\end{array}$

Calculate the average rate of change of the population from year $1950$ to $1990$ .

  $\begin{array}{c}\text{Average}=\frac{741368-48289}{1990-1950}\\ =\frac{693079}{40}\\ \approx 17327\end{array}$

Thus, the average rate of change of the population from year $1910$ to $1950$ is $1124$ persons per year and from year $1950$ to $1990$ is $17327$ persons per year.

b.

To graph: The scatter plot of the given data and appropriate regression graph.

The scatter plot of the given data is shown in figure (1) and appropriate regression is shown in figure (3).

Given information: The table below shows the population growth of Clark County:

Year	Population
$1910$	$3321$
$1920$	$4859$
$1930$	$8532$
$1940$	$16414$
$1950$	$48289$
$1960$	$127016$
$1970$	$273288$
$1980$	$463087$
$1990$	$741368$
$2000$	$1375741$
$2010$	$1951269$
$2016$	$2155664$

Graph:

To scatter plot of the given data in graphing calculator, under $\text{L}1$ enters the years from $1910$ to $2016$ and under $\text{L}2$ enter the population as shown below.

  

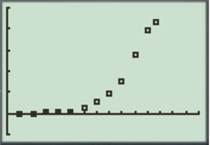
Figure (1)

To find the logistic equation from the given data, select $\text{Logistic}$ and press $\text{STAT}$ key.

  

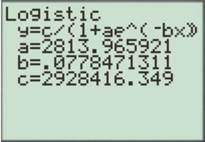
Figure (2)

The logistic equation of the given data is:

  $y=\frac{2928416.349}{1+2813.966e^{-0.07785x}}$

Now, draw the graph of the equation as shown below in the viewing window $\left[0,200\right]$ by $\left[-500000,3500000\right]$ .

  

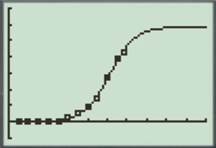
Figure (3)

Thus, the scatter plot of the given data is shown in figure (1) and appropriate regression is shown in figure (3).

c.

To find: The instantaneous rate of change of the population and the year in which fastest growth occur.

The instantaneous rate of change of the population is $56643$ and the growth occur fastest in the year $2000$ .

Given information: The table below shows the population growth of Clark County:

Year	Population
$1910$	$3321$
$1920$	$4859$
$1930$	$8532$
$1940$	$16414$
$1950$	$48289$
$1960$	$127016$
$1970$	$273288$
$1980$	$463087$
$1990$	$741368$
$2000$	$1375741$
$2010$	$1951269$
$2016$	$2155664$

Calculation:

From figure (3) in part (b), the curve grows fastest at $x=100$ or the year $2000$ .

Press $\text{MATH}$ key on the graphing calculator and select $\text{nDeriv}($ to find the numerical derivative of the function.

  

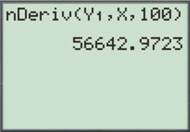
Figure (4)

Thus, the instantaneous rate of change of the population is $56643$ and the growth occur fastest in the year $2000$ .