
Concept explainers
A particle moves in a straight line with a constant acceleration of −4 ft/s2 for 6 s, zero acceleration for the next 4 s, and a constant acceleration of +4 ft/s2 for the next 4 s. Knowing that the particle starts from the origin and that its velocity is −8 ft/s during the zero acceleration time interval, (a) construct the v−t and x−t curves for 0 ≤ t ≤ 14 s, (b) determine the position and the velocity of the particle and the total distance traveled when t = 14 s.
Fig. P11.61 and P11.62
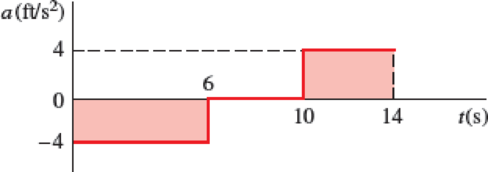
(a)
Construct the
Explanation of Solution
Given information:
The constant acceleration
The acceleration is zero from 6sec to 10 sec.
From 10 sec to 14 sec the acceleration
The velocity
Calculation:
Show a-t curve of particle that moves in a straight line as in Figure (1).
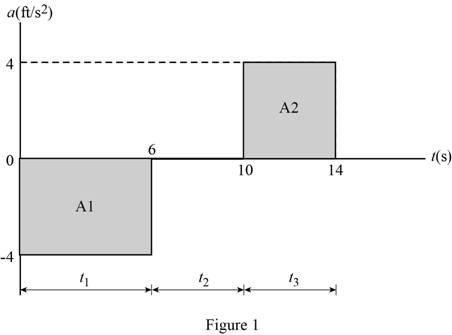
Calculate the area
Substitute 6 sec for
Calculate the area
Substitute 4 sec for
Calculate the velocity
Substitute
Calculate the velocity
Substitute
Calculate the velocity
Substitute
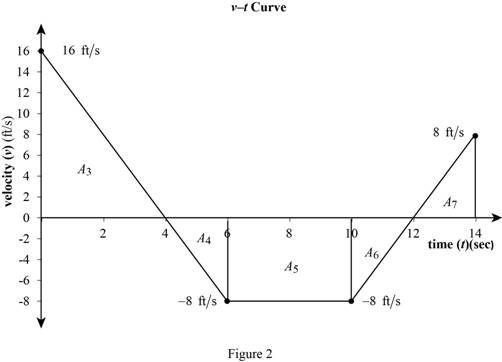
Tabulated the acceleration (a), velocity (v) corresponding to time (t) in Table (1) :
| t(s) | ||
| 0 | -4 | 16 |
| 6 | 0 | -8 |
| 10 | 0 | -8 |
| 14 | 4 | 8 |
Plot the v-t curve of particle that moves in a straight line with areas as in Figure (2).
Calculate the area
Here,
Substitute 4 sec for
Calculate the area
Here,
Substitute 2 sec for
Calculate the area
Here,
Substitute 4 sec for
Calculate the area
Here,
Substitute 2 sec for
Calculate the area
Here,
Substitute 4 sec for
Calculate the position
Calculate the position
Substitute 0 for
Calculate the position
Substitute
Calculate the position
Substitute
Calculate the position
Substitute
Calculate the position
Substitute
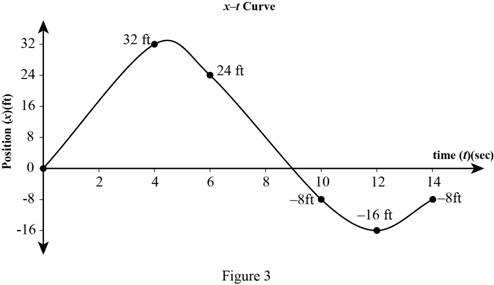
Tabulated the position (x) corresponding to time (t) in Table 2:
| t (sec) | x (ft) |
| 0 | 0 |
| 4 | 32 |
| 6 | 24 |
| 10 | -8 |
| 12 | -16 |
| 14 | -8 |
Plot x-t curve of particle that moves in a straight line with areas as in Figure 3.
(b)
The position, velocity of the particle and the total distance (d) traveled when time (t) 14 sec.
Answer to Problem 11.61P
The total distance (d) traveled when time (t) 14 sec is
Explanation of Solution
Given information:
The constant acceleration
The acceleration is zero from 6sec to 10 sec.
From 10 sec to 14 sec the acceleration
The velocity
Calculation:
Calculate the area
Substitute 6 sec for
Calculate the area
Substitute 4 sec for
Calculate the velocity
Substitute
Calculate the velocity
Substitute
Calculate the velocity
Substitute
Calculate the area
Here,
Substitute 4 sec for
Calculate the area
Here,
Substitute 2 sec for
Calculate the area
Here,
Substitute 4 sec for
Calculate the area
Here,
Substitute 2 sec for
Calculate the area
Here,
Substitute 4 sec for
Calculate the position
Calculate the position
Substitute 0 for
Calculate the position
Substitute
Calculate the position
Substitute
Calculate the position
Substitute
Calculate the position
Substitute
Calculate the distance
Substitute 0 for
Calculate the distance
Substitute
Calculate the distance
Substitute
Calculate the total distance (d) traveled when time (t) is 14 sec
Substitute
Therefore, the total distance (d) traveled when time (t) 14 sec is
Want to see more full solutions like this?
Chapter 11 Solutions
Connect 1 Semester Access Card for Vector Mechanics for Engineers: Statics and Dynamics
- Q1/ A vertical, circular gate with water on one side as shown. Determine the total resultant force acting on the gate and the location of the center of pressure, use water specific weight 9.81 kN/m³ 1 m 4 marrow_forwardI need handwritten solution with sketches for eacharrow_forwardGiven answers to be: i) 14.65 kN; 6.16 kN; 8.46 kN ii) 8.63 kN; 9.88 kN iii) Bearing 6315 for B1 & B2, or Bearing 6215 for B1arrow_forward
- (b) A steel 'hot rolled structural hollow section' column of length 5.75 m, has the cross-section shown in Figure Q.5(b) and supports a load of 750 kN. During service, it is subjected to axial compression loading where one end of the column is effectively restrained in position and direction (fixed) and the other is effectively held in position but not in direction (pinned). i) Given that the steel has a design strength of 275 MN/m², determine the load factor for the structural member based upon the BS5950 design approach using Datasheet Q.5(b). [11] ii) Determine the axial load that can be supported by the column using the Rankine-Gordon formula, given that the yield strength of the material is 280 MN/m² and the constant *a* is 1/30000. [6] 300 600 2-300 mm wide x 5 mm thick plates. Figure Q.5(b) L=5.75m Pinned Fixedarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forward
- Q2: For the following figure, find the reactions of the system. The specific weight of the plate is 500 lb/ft³arrow_forwardQ1: For the following force system, find the moments with respect to axes x, y, and zarrow_forwardQ10) Body A weighs 600 lb contact with smooth surfaces at D and E. Determine the tension in the cord and the forces acting on C on member BD, also calculate the reaction at B and F. Cable 6' 3' wwwarrow_forward
- Help ارجو مساعدتي في حل هذا السؤالarrow_forwardQ3: Find the resultant of the force system.arrow_forwardQuestion 1 A three-blade propeller of a diameter of 2 m has an activity factor AF of 200 and its ratio of static thrust coefficient to static torque coefficient is 10. The propeller's integrated lift coefficient is 0.3.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





