A Problem Solving Approach to Mathematics for Elementary School Teachers (12th Edition)
12th Edition
ISBN: 9780321987297
Author: Rick Billstein, Shlomo Libeskind, Johnny Lott
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 11.2A, Problem 1A
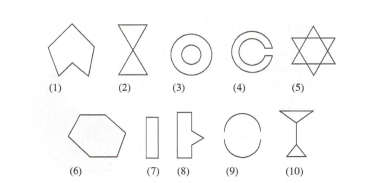
Determine which of the following figures labeled (1) through (10) can be classified under the given description.
a. Simple closed curve
b.
c. Convex polygon
d. Concave polygon
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
In a volatile housing market, the overall value of a home can be modeled by V(x) = 415x² - 4600x + 200000, where V represents the value of the home and x represents each year after 2020.
Part A: Find the vertex of V(x). Show all work.
Part B: Interpret what the vertex means in terms of the value of the home.
Show all work to solve 3x² + 5x - 2 = 0.
Two functions are given below: f(x) and h(x). State the axis of symmetry for each function and explain how to find it.
f(x)
h(x)
21
5
4+
3
f(x) = −2(x − 4)² +2
+
-5 -4-3-2-1
1
2
3
4
5
-1
-2
-3
5
Chapter 11 Solutions
A Problem Solving Approach to Mathematics for Elementary School Teachers (12th Edition)
Ch. 11.1 - Answer each of the following and explain your...Ch. 11.1 - Given a line and a point not on the line, explain...Ch. 11.1 - How are pairs of parallel lines and skew lines a....Ch. 11.1 - Is it possible for ABC to have vertex C? Why?Ch. 11.1 - If planes and are distinct planes having points...Ch. 11.1 - Prob. 7MCCh. 11.1 - MATHEMATICAL CONNECTIONS A line n is perpendicular...Ch. 11.1 - MATHEMATICAL CONNECTIONS a. Sketch three rays that...Ch. 11.1 - Identify a physical object within the classroom to...Ch. 11.1 - Prob. 12MC
Ch. 11.1 - Let each member of your group use a protractor to...Ch. 11.1 - Allie says that AB and CD are parallel because...Ch. 11.1 - Prob. 15MCCh. 11.1 - A student says that ABBA because AB starts at A...Ch. 11.1 - Prob. 17MCCh. 11.1 - A student claims that if any two planes that do...Ch. 11.1 - A student says that it is actually impossible to...Ch. 11.1 - Prob. 20MCCh. 11.1 - A student says there can be only 360 different...Ch. 11.1 - What is the intersection of rays PQ and QP in the...Ch. 11.1 - Lines a and b are parallel to each other. Lines c...Ch. 11.1 - Prob. 3NAEPCh. 11.1A - Name two rays that contain a. BC. b. EG.Ch. 11.1A - Let S be the set of lines, skew to a given line,...Ch. 11.1A - Label each of the following as true or false. If...Ch. 11.1A - a. Points A,B,C and D are collinear. In how many...Ch. 11.1A - The following figure is a rectangular box in which...Ch. 11.1A - Assessment Use the following drawing of one of the...Ch. 11.1A - ASSESSMENT Determine how many acute angles are...Ch. 11.1A - Identify a physical model for each of the...Ch. 11.1A - Find the measure of each of the following angles....Ch. 11.1A - Assessment a. Perform each of the following...Ch. 11.1A - Assessment Consider a correctly set clock that...Ch. 11.1A - In parts a and b of the following figures,...Ch. 11.1A - Given three collinear points A,B,C with B between...Ch. 11.1A - Prob. 14ACh. 11.1A - ASSESSMENT Trace each of the following drawings....Ch. 11.1A - Prob. 17ACh. 11.1A - Prob. 18ACh. 11.1B - ASSESSMENT Name three points that are not...Ch. 11.1B - Let C be the set of coplanar lines with a given...Ch. 11.1B - Prob. 4ACh. 11.1B - ASSESSMENT The following figure is a box in which...Ch. 11.1B - Prob. 6ACh. 11.1B - ASSESSMENT Determine the number of obtuse angles...Ch. 11.1B - Identify a physical model for each of the...Ch. 11.1B - ASSESSMENT Find the measures of each of the...Ch. 11.1B - a. Perform a following operations. Leave your...Ch. 11.1B - Prob. 11ACh. 11.1B - Assessment In each of the following figures,...Ch. 11.1B - ASSESSMENT In each of the following pairs,...Ch. 11.1B - Prob. 15ACh. 11.1B - ASSESSMENT On the dot paper below, draw all...Ch. 11.1B - ASSESSMENT In the figure below, O is the center of...Ch. 11.1B - If the measure of A is 30 more than twice the...Ch. 11.1B - ASSESSMENT Describe each of the following sets of...Ch. 11.2 - Prob. 1MCCh. 11.2 - Can a regular polygon be concave? Explain.Ch. 11.2 - Prob. 3MCCh. 11.2 - Classify each of the following as true or false....Ch. 11.2 - MATHEMATICAL CONNECTIONS Copy and complete...Ch. 11.2 - MATHEMATICAL CONNECTIONS On a geoboard or dot...Ch. 11.2 - Work with partners to create a Venn diagram with...Ch. 11.2 - Work with partners to create a Venn diagram...Ch. 11.2 - The six pattern blocks shown below are...Ch. 11.2 - Prob. 12MCCh. 11.2 - Prob. 13MCCh. 11.2 - Millie claims that a rhombus is regular because...Ch. 11.2 - Jane heard a student say that all squares are...Ch. 11.2 - A student asks if ABCD is a valid name for the...Ch. 11.2 - MATHEMATICAL CONNECTIONS A student claims that all...Ch. 11.2 - MATHEMATICAL CONNECTIONS Two students are thinking...Ch. 11.2 - Use GeoGebra Lab-2 to construct quadrilaterals.Ch. 11.2 - If three distinct rays with the same vertex are...Ch. 11.2 - Prob. 21MCCh. 11.2 - Prob. 22MCCh. 11.2 - Prob. 1NAEPCh. 11.2 - NATIONAL ASSESSMENT OF EDUCATIONAL PROGRESS NAEP...Ch. 11.2A - Determine which of the following figures labeled 1...Ch. 11.2A - What is the maximum number of intersection points...Ch. 11.2A - What type of polygon must have a diagonal such...Ch. 11.2A - Describe the shaded region as simply as possible.Ch. 11.2A - If possible, draw the following triangles. If it...Ch. 11.2A - Determine how many diagonals each of the following...Ch. 11.2A - Draw all lines of symmetry if any exist for each...Ch. 11.2A - Identify each of the following triangles as...Ch. 11.2A - Various international signs have symmetries....Ch. 11.2A - Prob. 11ACh. 11.2A - Design symbols that have each of the following...Ch. 11.2A - In each of the following figures, complete the...Ch. 11.2A - Prob. 14ACh. 11.2A - Prob. 15ACh. 11.2A - Complete the following figures so that they have...Ch. 11.2A - Prob. 17ACh. 11.2B - ASSESSMENT Determine which of the following...Ch. 11.2B - ASSESSMENT What is the maximum number of...Ch. 11.2B - ASSESSMENT A pentagon has only two diagonals that...Ch. 11.2B - ASSESSMENT Which of the following figures are...Ch. 11.2B - ASSESSMENT Describe the shaded region as simply as...Ch. 11.2B - Prob. 6ACh. 11.2B - Prob. 7ACh. 11.2B - Prob. 8ACh. 11.2B - ASSESSMENT Identify each of the following...Ch. 11.2B - Prob. 10ACh. 11.2B - Prob. 11ACh. 11.2B - Prob. 12ACh. 11.2B - Prob. 13ACh. 11.2B - Prob. 14ACh. 11.2B - Prob. 15ACh. 11.2B - Prob. 16ACh. 11.2B - Prob. 17ACh. 11.3 - Prob. 1MCCh. 11.3 - Prob. 2MCCh. 11.3 - Prob. 3MCCh. 11.3 - Prob. 4MCCh. 11.3 - Prob. 5MCCh. 11.3 - Prob. 6MCCh. 11.3 - Prob. 7MCCh. 11.3 - Prob. 8MCCh. 11.3 - Regular hexagons have been used to tile floors....Ch. 11.3 - Lines a and b are cut by transversals c and d. If...Ch. 11.3 - A beam of light from A hits the surface of a...Ch. 11.3 - Find a possible set of measures of the interior...Ch. 11.3 - Draw three different concave polygons. When you...Ch. 11.3 - Draw three concave polygons. Measure all the...Ch. 11.3 - Prob. 15MCCh. 11.3 - Prob. 16MCCh. 11.3 - Jan wants to make tiles in the shape of a convex...Ch. 11.3 - A student wonders if there exists a convex decagon...Ch. 11.3 - A student wants to know if a triangle can have two...Ch. 11.3 - In each of the following, name the required...Ch. 11.3 - Prob. 21MCCh. 11.3 - Prob. 22MCCh. 11.3 - Design symbols that have each of the following...Ch. 11.3 - Prob. 24MCCh. 11.3 - Explain whether the following quilt patterns have...Ch. 11.3 - Find the lines of symmetry, if any, for each of...Ch. 11.3 - Prob. 1NAEPCh. 11.3 - In the given figure, what is the measure of angle...Ch. 11.3 - Prob. 3NAEPCh. 11.3A - If three lines all meet in a single point, how...Ch. 11.3A - Prob. 2ACh. 11.3A - Find the measure of a complementary angle, a...Ch. 11.3A - Assessment In ABC, the measure of B is three times...Ch. 11.3A - Prob. 5ACh. 11.3A - Prob. 6ACh. 11.3A - Prob. 7ACh. 11.3A - Prob. 8ACh. 11.3A - Prob. 9ACh. 11.3A - Prob. 10ACh. 11.3A - Find the sum of the measures of the numbered...Ch. 11.3A - Prob. 12ACh. 11.3A - Prob. 13ACh. 11.3A - Prob. 14ACh. 11.3A - Prob. 15ACh. 11.3A - Prob. 16ACh. 11.3A - Prob. 17ACh. 11.3A - Find the measures of ange 1, 2, and 3 given that...Ch. 11.3A - Prob. 19ACh. 11.3A - Prob. 20ACh. 11.3A - Prob. 21ACh. 11.3A - Assessment 11-3A If m(2)=m(3), prove m(1)=m(4).Ch. 11.3B - If two planes intersect in a single line forming...Ch. 11.3B - Assessment 11-3B Find the measures of angle marked...Ch. 11.3B - Prob. 3ACh. 11.3B - Assessment 11-3B An angle measures 15 more than 4...Ch. 11.3B - Prob. 5ACh. 11.3B - Prob. 6ACh. 11.3B - Prob. 7ACh. 11.3B - In part (a), prove that kl .In parts (b)and(c),...Ch. 11.3B - Prob. 9ACh. 11.3B - Prob. 10ACh. 11.3B - Prob. 11ACh. 11.3B - Calculate the measure of each angle of a pentagon,...Ch. 11.3B - The sides of DEF are parallel to the sides of BCA....Ch. 11.3B - In each of the following figures, find the...Ch. 11.3B - Prob. 15ACh. 11.3B - Prob. 16ACh. 11.3B - Prob. 17ACh. 11.3B - Find the measure of x in the figure below.Ch. 11.3B - Prob. 19ACh. 11.3B - Prob. 20ACh. 11.3B - Given the figure shown with AXDY, find the...Ch. 11.3B - Prob. 22ACh. 11.4 - How many possible pairs of bases does a right...Ch. 11.4 - Prob. 2MCCh. 11.4 - Prob. 3MCCh. 11.4 - What is the name of a pyramid that has 9 vertices?Ch. 11.4 - Prob. 5MCCh. 11.4 - What is the minimum number of faces that intersect...Ch. 11.4 - Sketch at least 2 nets for the prism shown below.Ch. 11.4 - Prob. 11MCCh. 11.4 - Prob. 12MCCh. 11.4 - Prob. 13MCCh. 11.4 - Prob. 14MCCh. 11.4 - Prob. 15MCCh. 11.4 - Prob. 17MCCh. 11.4 - Prob. 18MCCh. 11.4 - Prob. 19MCCh. 11.4 - Find the supplement of 181342.Ch. 11.4 - Prob. 21MCCh. 11.4 - Can two adjacent angles be vertical angles?...Ch. 11.4 - How many diagonals are there in a decagon?Ch. 11.4 - In a regular 20-gon, what is the measure of each...Ch. 11.4 - If mn find m(1).Ch. 11.4 - Which of the following can be folded to form the...Ch. 11.4 - Kyle makes a 3-dimensional shape using 3...Ch. 11.4 - Prob. 3NAEPCh. 11.4 - The figure above shown a pyramid with a square...Ch. 11.4A - Identify each of the following polyhedral. If a...Ch. 11.4A - Prob. 2ACh. 11.4A - Given the tetrahedron shown, name the following....Ch. 11.4A - Prob. 4ACh. 11.4A - Prob. 5ACh. 11.4A - Prob. 6ACh. 11.4A - Classify each of the following statements as true...Ch. 11.4A - Prob. 8ACh. 11.4A - Prob. 9ACh. 11.4A - Sketch a pyramid that is hexahedron six facesCh. 11.4A - Prob. 11ACh. 11.4A - Prob. 12ACh. 11.4A - Prob. 13ACh. 11.4A - Prob. 14ACh. 11.4A - Prob. 15ACh. 11.4A - Prob. 16ACh. 11.4A - Name the intersection of each of the following...Ch. 11.4A - Prob. 18ACh. 11.4A - Prob. 19ACh. 11.4A - Prob. 20ACh. 11.4B - Identify each of the following three-dimensional...Ch. 11.4B - The following are pictures of solid cubes lying on...Ch. 11.4B - Prob. 4ACh. 11.4B - Prob. 5ACh. 11.4B - Determine the minimum number of edges possible for...Ch. 11.4B - Prob. 8ACh. 11.4B - Prob. 9ACh. 11.4B - Prob. 10ACh. 11.4B - Name the polyhedron that can be constructed using...Ch. 11.4B - Prob. 13ACh. 11.4B - Prob. 14ACh. 11.4B - Prob. 15ACh. 11.4B - On the left of each of the following figure is a...Ch. 11.4B - Prob. 17ACh. 11.4B - Prob. 18ACh. 11.4B - Answer each of the following questions about a...Ch. 11.4B - A diagonal of a prism is any segment determined by...Ch. 11.4B - A soccer ball resembles a polyhedron with 32 faces...Ch. 11.CR - Prob. 1CRCh. 11.CR - Prob. 3CRCh. 11.CR - Prob. 4CRCh. 11.CR - Prob. 5CRCh. 11.CR - a. Can a triangle have two obtuse angles? Justify...Ch. 11.CR - In a certain triangle, the measure of one angle is...Ch. 11.CR - If ABC is a right angles triangle and m(A)=42,...Ch. 11.CR - Prob. 9CRCh. 11.CR - Prob. 10CRCh. 11.CR - Prob. 11CRCh. 11.CR - Prob. 12CRCh. 11.CR - Prob. 13CRCh. 11.CR - Prob. 14CRCh. 11.CR - Prob. 15CRCh. 11.CR - Prob. 16CRCh. 11.CR - Prob. 18CRCh. 11.CR - Prob. 19CRCh. 11.CR - Prob. 20CRCh. 11.CR - Prob. 21CRCh. 11.CR - Prob. 22CRCh. 11.CR - Prob. 23CRCh. 11.CR - Prob. 24CRCh. 11.CR - In each of the following figures, determine the...Ch. 11.CR - Prob. 26CRCh. 11.CR - Prob. 28CRCh. 11.CR - In the figure below, ab. Find the following...Ch. 11.CR - Prob. 30CRCh. 11.CR - Carefully draw nets that can be folded into each...Ch. 11.CR - Prob. 32CRCh. 11.CR - Prob. 33CRCh. 11 - Just as a point separates a line into three parts,...Ch. 11 - a. Can skew lines have a point in common? Why? b....Ch. 11 - Now try this Convert 8.42 to degrees, minutes and...Ch. 11 - Prob. 6NTCh. 11 - Prob. 7NTCh. 11 - Prob. 8NTCh. 11 - Use the definitions in Table 8 and several...Ch. 11 - Prob. 11NTCh. 11 - Prob. 12NTCh. 11 - Prob. 13NT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- The functions f(x) = (x + 1)² - 2 and g(x) = (x-2)² + 1 have been rewritten using the completing-the-square method. Apply your knowledge of functions in vertex form to determine if the vertex for each function is a minimum or a maximum and explain your reasoning.arrow_forwardTotal marks 15 3. (i) Let FRN Rm be a mapping and x = RN is a given point. Which of the following statements are true? Construct counterex- amples for any that are false. (a) If F is continuous at x then F is differentiable at x. (b) If F is differentiable at x then F is continuous at x. If F is differentiable at x then F has all 1st order partial (c) derivatives at x. (d) If all 1st order partial derivatives of F exist and are con- tinuous on RN then F is differentiable at x. [5 Marks] (ii) Let mappings F= (F1, F2) R³ → R² and G=(G1, G2) R² → R² : be defined by F₁ (x1, x2, x3) = x1 + x², G1(1, 2) = 31, F2(x1, x2, x3) = x² + x3, G2(1, 2)=sin(1+ y2). By using the chain rule, calculate the Jacobian matrix of the mapping GoF R3 R², i.e., JGoF(x1, x2, x3). What is JGOF(0, 0, 0)? (iii) [7 Marks] Give reasons why the mapping Go F is differentiable at (0, 0, 0) R³ and determine the derivative matrix D(GF)(0, 0, 0). [3 Marks]arrow_forward5. (i) Let f R2 R be defined by f(x1, x2) = x² - 4x1x2 + 2x3. Find all local minima of f on R². (ii) [10 Marks] Give an example of a function f: R2 R which is not bounded above and has exactly one critical point, which is a minimum. Justify briefly Total marks 15 your answer. [5 Marks]arrow_forward
- Total marks 15 4. : Let f R2 R be defined by f(x1, x2) = 2x²- 8x1x2+4x+2. Find all local minima of f on R². [10 Marks] (ii) Give an example of a function f R2 R which is neither bounded below nor bounded above, and has no critical point. Justify briefly your answer. [5 Marks]arrow_forward4. Let F RNR be a mapping. (i) x ЄRN ? (ii) : What does it mean to say that F is differentiable at a point [1 Mark] In Theorem 5.4 in the Lecture Notes we proved that if F is differentiable at a point x E RN then F is continuous at x. Proof. Let (n) CRN be a sequence such that xn → x ЄERN as n → ∞. We want to show that F(xn) F(x), which means F is continuous at x. Denote hnxn - x, so that ||hn|| 0. Thus we find ||F(xn) − F(x)|| = ||F(x + hn) − F(x)|| * ||DF (x)hn + R(hn) || (**) ||DF(x)hn||+||R(hn)||| → 0, because the linear mapping DF(x) is continuous and for all large nЄ N, (***) ||R(hn) || ||R(hn) || ≤ → 0. ||hn|| (a) Explain in details why ||hn|| → 0. [3 Marks] (b) Explain the steps labelled (*), (**), (***). [6 Marks]arrow_forward4. In Theorem 5.4 in the Lecture Notes we proved that if F: RN → Rm is differentiable at x = RN then F is continuous at x. Proof. Let (xn) CRN be a sequence such that x → x Є RN as n → ∞. We want F(x), which means F is continuous at x. to show that F(xn) Denote hn xnx, so that ||hn||| 0. Thus we find ||F (xn) − F(x) || (*) ||F(x + hn) − F(x)|| = ||DF(x)hn + R(hn)|| (**) ||DF(x)hn|| + ||R(hn) || → 0, because the linear mapping DF(x) is continuous and for all large n = N, |||R(hn) || ≤ (***) ||R(hn)|| ||hn|| → 0. Explain the steps labelled (*), (**), (***) [6 Marks] (ii) Give an example of a function F: RR such that F is contin- Total marks 10 uous at x=0 but F is not differentiable at at x = 0. [4 Marks]arrow_forward
- 3. Let f R2 R be a function. (i) Explain in your own words the relationship between the existence of all partial derivatives of f and differentiability of f at a point x = R². (ii) Consider R2 → R defined by : [5 Marks] f(x1, x2) = |2x1x2|1/2 Show that af af -(0,0) = 0 and -(0, 0) = 0, Jx1 მx2 but f is not differentiable at (0,0). [10 Marks]arrow_forward13) Consider the checkerboard arrangement shown below. Assume that the red checker can move diagonally upward, one square at a time, on the white squares. It may not enter a square if occupied by another checker, but may jump over it. How many routes are there for the red checker to the top of the board?arrow_forwardFill in the blanks to describe squares. The square of a number is that number Question Blank 1 of 4 . The square of negative 12 is written as Question Blank 2 of 4 , but the opposite of the square of 12 is written as Question Blank 3 of 4 . 2 • 2 = 4. Another number that can be multiplied by itself to equal 4 is Question Blank 4 of 4 .arrow_forward
- 12) The prime factors of 1365 are 3, 5, 7 and 13. Determine the total number of divisors of 1365.arrow_forward11) What is the sum of numbers in row #8 of Pascal's Triangle?arrow_forward14) Seven students and three teachers wish to join a committee. Four of them will be selected by the school administration. What is the probability that three students and one teacher will be selected?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Propositional Logic, Propositional Variables & Compound Propositions; Author: Neso Academy;https://www.youtube.com/watch?v=Ib5njCwNMdk;License: Standard YouTube License, CC-BY
Propositional Logic - Discrete math; Author: Charles Edeki - Math Computer Science Programming;https://www.youtube.com/watch?v=rL_8y2v1Guw;License: Standard YouTube License, CC-BY
DM-12-Propositional Logic-Basics; Author: GATEBOOK VIDEO LECTURES;https://www.youtube.com/watch?v=pzUBrJLIESU;License: Standard Youtube License
Lecture 1 - Propositional Logic; Author: nptelhrd;https://www.youtube.com/watch?v=xlUFkMKSB3Y;License: Standard YouTube License, CC-BY
MFCS unit-1 || Part:1 || JNTU || Well formed formula || propositional calculus || truth tables; Author: Learn with Smily;https://www.youtube.com/watch?v=XV15Q4mCcHc;License: Standard YouTube License, CC-BY