Mathematics for Elementary Teachers with Activities, Books a la carte edition (5th Edition)
5th Edition
ISBN: 9780134423319
Author: Sybilla Beckmann
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 11.2, Problem 4P
Describe one-dlmenslonal, two-dlmenslonal, and three dimensional parts or aspects of the blocks in Figure 11.11 . In each case. compare the sizes of the 3 blocks, using an appropriate unit. Use this unit to show that each block can be considered biggest of all 3.
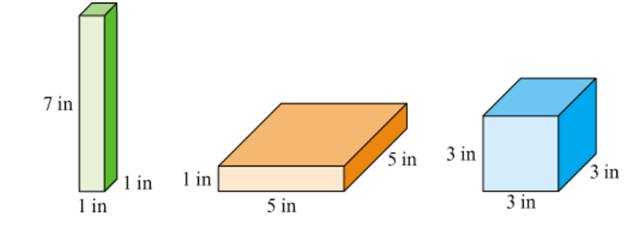
Flgure 11.11 Which block ls biggest?
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
solve the system of equations
30% of all college students major in STEM (Science, Technology, Engineering, and Math). If 48 college students are randomly selected, find the probability thata. Exactly 12 of them major in STEM. b. At most 17 of them major in STEM. c. At least 12 of them major in STEM. d. Between 9 and 13 (including 9 and 13) of them major in STEM.
7% of all Americans live in poverty. If 40 Americans are randomly selected, find the probability thata. Exactly 4 of them live in poverty. b. At most 1 of them live in poverty. c. At least 1 of them live in poverty. d. Between 2 and 9 (including 2 and 9) of them live in poverty.
Chapter 11 Solutions
Mathematics for Elementary Teachers with Activities, Books a la carte edition (5th Edition)
Ch. 11.1 - For each of the following metric units, give...Ch. 11.1 - For each of the following items, state which U.S....Ch. 11.1 - What does it mean to say that a shape has an area...Ch. 11.1 - Discuss why it is easy to give an incorrect...Ch. 11.1 - Discuss: Why is it not completely correct to...Ch. 11.1 - Describe how it could happen that three different...Ch. 11.1 - Pick two ideas or concepts from your reading of...Ch. 11.1 - Visit a store and write down at least 10 different...Ch. 11.2 - Describe one-dimensional, two-dimensional, and...Ch. 11.2 - Describe one-dimensional, two-dimensional, and...
Ch. 11.2 - Drawing on your reading from this section,...Ch. 11.2 - Describe one-dlmenslonal, two-dlmenslonal, and...Ch. 11.2 - The Lazy Daze Pool Club and the Slumber-N-Sunshine...Ch. 11.2 - Suppose there are 2 rectangular pools: One is 30...Ch. 11.2 - Minh says that the rectangle on the left in Flgure...Ch. 11.3 - One source says that the average distance from the...Ch. 11.3 - If an object is described as weighing 6.20 grams,...Ch. 11.3 - Tyra ls calculating the distance from town A to...Ch. 11.3 - John has a paper square that he believes is 100 cm...Ch. 11.3 - Sally has a Plexiglas cube that she believes is...Ch. 11.4 - A recipe calls tor 4 ounces ot chocolate. If you...Ch. 11.4 - A class needs 27 pieces of ribbon, each piece 2...Ch. 11.4 - To convert 24 yards to feet, should you multiply...Ch. 11.4 - To convert 2000 kilometers to meters, should you...Ch. 11.4 - Shauntay used identical plastic bears to measure...Ch. 11.4 - A car is 16 feet, 3 inches long. How long is it in...Ch. 11.4 - The distance between two cities is described as...Ch. 11.4 - In Germany, people often drive 130 kilometers per...Ch. 11.4 - One foot is 12 inches. Does this mean that 1...Ch. 11.4 - A room has a floor area of 48 square yards. What...Ch. 11.4 - One kilometer is 1000 meters. Does this mean that...Ch. 11.4 - One foot is 12 inches. Does this mean that 1 cubic...Ch. 11.4 - How much mulch will you need to cover a...Ch. 11.4 - A classroom has a floor area of 600 square feet....Ch. 11.4 - A house has a floor area of 800 square meters....Ch. 11.4 - A house has a floor area of 250 square meters....Ch. 11.4 - The Smiths will be carpeting a room in their...Ch. 11.4 - One acre is 43,560 square feet. If a square piece...Ch. 11.4 - A construction company has dump trucks that hold...Ch. 11.4 - The following questlon explores why It doesn’t...Ch. 11.4 - A penny is 116 of an inch thick. Suppose you have...Ch. 11.4 - Write 100 zeros on a piece of paper and time how...Ch. 11.4 - For a certain type of rice, about 50 grains till a...Ch. 11.4 - Assuming that 1 gram of gold is worth $30 how much...Ch. 11.4 - Imagine that all the people on earth could stand...Ch. 11.4 - Joey has a toy car that is a 1: 64 scale model of...
Additional Math Textbook Solutions
Find more solutions based on key concepts
23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...
College Algebra (Collegiate Math)
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
Provide an example of a qualitative variable and an example of a quantitative variable.
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
Find E(X) for each of the distributions given in Exercise 2.1-3.
Probability And Statistical Inference (10th Edition)
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 48% of all violent felons in the prison system are repeat offenders. If 40 violent felons are randomly selected, find the probability that a. Exactly 18 of them are repeat offenders. b. At most 18 of them are repeat offenders. c. At least 18 of them are repeat offenders. d. Between 17 and 21 (including 17 and 21) of them are repeat offenders.arrow_forwardNo chatgpt pls will upvotearrow_forwardQ. A: For any set A define the set -A=(y R13x A such that y=-x). Prove that if A c R is non-empty and bounded then sup(-A) = -inf(A). Qi, B: State and Prove Monotone Convergence Theorem. Q. C. Prove that for any irrational number, there exists a sequence of rational numbers (x) converging to . Aarrow_forward
- 4. Some psychologists contend that the number of facts of a certain type that are remembered after t hours is given by f(t)== 90t 951-90 Find the rate at which the number of facts remembered is changing after 1 hour and after 10 hours. Interpret.arrow_forward12:05 MA S 58 58. If f(x) = ci.metaproxy.org 25 2xon [0, 10] and n is a positive integer, then there is some Riemann sum Sthat equals the exact area under the graph of ƒ from x = Oto x = 10. 59. If the area under the graph of fon [a, b] is equal to both the left sum L, and the right sum Rfor some positive integer n, then fis constant on [a, b]. 60. If ƒ is a decreasing function on [a, b], then the area under the graph of fis greater than the left sum Land less than the right sum R₂, for any positive integer n. Problems 61 and 62 refer to the following figure showing two parcels of land along a river: River Parcel 2 Parcel 1 h(x) 500 ft 1,000 ft. Figure for 61 and 62 61. You want to purchase both parcels of land shown in the figure and make a quick check on their combined area. There is no equation for the river frontage, so you use the average of the left and right sums of rectangles covering the area. The 1,000-foot baseline is divided into 10 equal parts. At the end of each…arrow_forwardStan(x)√√2+ √√4 59 4 + cos(x)dxarrow_forward
- No chatgpt pls will upvotearrow_forwardIf a snowball melts so that its surface area decreases at a rate of 10 cm²/min, find the rate (in cm/min) at which the diameter decreases when the diameter is 12 cm. (Round your answer to three decimal places.) cm/minarrow_forwardया it 11 if the mechanism is given, then using Newton's posterior formula for the derivative Lind P(0.9) × 0 0.2 0.4 0.6 0.8 1 f 0 0.12 0.48 1.1 2 3.2arrow_forward
- Consider an MA(6) model with θ1 = 0.5, θ2 = −25, θ3 = 0.125, θ4 = −0.0625, θ5 = 0.03125, and θ6 = −0.015625. Find a much simpler model that has nearly the same ψ-weights.arrow_forwardLet {Yt} be an AR(2) process of the special form Yt = φ2Yt − 2 + et. Use first principles to find the range of values of φ2 for which the process is stationary.arrow_forwardDescribe the important characteristics of the autocorrelation function for the following models: (a) MA(1), (b) MA(2), (c) AR(1), (d) AR(2), and (e) ARMA(1,1).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Write the Complex Number in Trigonometric (Polar) Form; Author: The Math Sorcerer;https://www.youtube.com/watch?v=9kZOHHRjfIQ;License: Standard YouTube License, CC-BY