MYLAB W/ETEXT FOR MATHEMATICS ALL AROUN
6th Edition
ISBN: 9780135902783
Author: Pirnot
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 11.2, Problem 3E
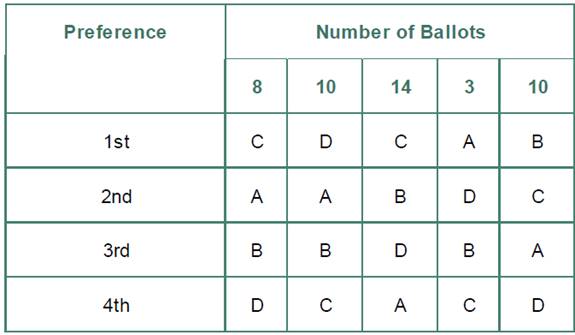
Determining the legal drinking age. A state commission is voting on changing the legal drinking age. The options are A, lower the age to 18; B, lower the age to 19; C, lower the age to 20; and D, keep the age at 21. Use the preference table to determine the winner using the Borda count method. Show that Condorcet’s criterion is not satisfied.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
12:25 AM Sun Dec 22
uestion 6- Week 8: QuX
Assume that a company X +
→ C
ezto.mheducation.com
Week 8: Quiz i
Saved
6
4
points
Help
Save & Exit
Submit
Assume that a company is considering purchasing a machine for $50,000 that will have a five-year useful life and a $5,000 salvage value. The
machine will lower operating costs by $17,000 per year. The company's required rate of return is 15%. The net present value of this investment
is closest to:
Click here to view Exhibit 12B-1 and Exhibit 12B-2, to determine the appropriate discount factor(s) using the tables provided.
00:33:45
Multiple Choice
О
$6,984.
$11,859.
$22,919.
○ $9,469,
Mc
Graw
Hill
2
100-
No chatgpt pls will upvote
7. [10 marks]
Let G
=
(V,E) be a 3-connected graph. We prove that for every x, y, z Є V, there is a
cycle in G on which x, y, and z all lie.
(a) First prove that there are two internally disjoint xy-paths Po and P₁.
(b) If z is on either Po or P₁, then combining Po and P₁ produces a cycle on which
x, y, and z all lie. So assume that z is not on Po and not on P₁. Now prove that
there are three paths Qo, Q1, and Q2 such that:
⚫each Qi starts at z;
• each Qi ends at a vertex w; that is on Po or on P₁, where wo, w₁, and w₂ are
distinct;
the paths Qo, Q1, Q2 are disjoint from each other (except at the start vertex
2) and are disjoint from the paths Po and P₁ (except at the end vertices wo,
W1, and w₂).
(c) Use paths Po, P₁, Qo, Q1, and Q2 to prove that there is a cycle on which x, y, and
z all lie. (To do this, notice that two of the w; must be on the same Pj.)
Chapter 11 Solutions
MYLAB W/ETEXT FOR MATHEMATICS ALL AROUN
Ch. 11.1 - Four candidates running for a vacant seat on the...Ch. 11.1 - Five candidates running for mayor receive votes as...Ch. 11.1 - The university administration has asked a group of...Ch. 11.1 - The university administration has asked a group of...Ch. 11.1 - The university administration has asked a group of...Ch. 11.1 - The university administration has asked a group of...Ch. 11.1 - The drama society members are voting for the type...Ch. 11.1 - The drama society members are voting for the type...Ch. 11.1 - The drama society members are voting for the type...Ch. 11.1 - The drama society members are voting for the type...
Ch. 11.1 - Before a conference on Trends in the next Decade,...Ch. 11.1 - Before a conference on Trends in the next Decade,...Ch. 11.1 - Prob. 13ECh. 11.1 - Prob. 14ECh. 11.1 - A small employee-owned Internet company is voting...Ch. 11.1 - Prob. 16ECh. 11.1 - Prob. 17ECh. 11.1 - A small employee-owned Internet company is voting...Ch. 11.1 - Prob. 19ECh. 11.1 - Prob. 20ECh. 11.1 - Prob. 21ECh. 11.1 - Prob. 22ECh. 11.1 - In Exercises 23-26, refer to the preference table...Ch. 11.1 - Prob. 24ECh. 11.1 - In Exercises 23-26, refer to the preference table...Ch. 11.1 - Prob. 26ECh. 11.1 - In Exercises 27-30, refer to the preference table...Ch. 11.1 - In Exercises 27-30, refer to the preference table...Ch. 11.1 - In Exercises 27-30, refer to the preference table...Ch. 11.1 - Prob. 30ECh. 11.1 - Prob. 31ECh. 11.1 - Prob. 32ECh. 11.1 - Prob. 33ECh. 11.1 - Prob. 34ECh. 11.1 - Prob. 35ECh. 11.1 - Prob. 36ECh. 11.1 - Prob. 37ECh. 11.1 - Prob. 38ECh. 11.1 - Prob. 39ECh. 11.1 - Prob. 40ECh. 11.1 - Prob. 41ECh. 11.1 - Prob. 42ECh. 11.1 - Prob. 43ECh. 11.1 - Math in Your Life: Between the Numbers Instant...Ch. 11.1 - In approval voting, a person can vote for more...Ch. 11.1 - Prob. 46ECh. 11.1 - Prob. 47ECh. 11.1 - Prob. 48ECh. 11.1 - Prob. 49ECh. 11.1 - Prob. 50ECh. 11.1 - Prob. 51ECh. 11.1 - Prob. 52ECh. 11.2 - Some of these exercises have no fixed solution...Ch. 11.2 - Some of these exercises have no fixed solution...Ch. 11.2 - Determining the legal drinking age. A state...Ch. 11.2 - Voting for the president of a club. A chapter of...Ch. 11.2 - Choosing a location for a research facility. Teach...Ch. 11.2 - Locating a new factory. The Land Mover Tractor...Ch. 11.2 - Reducing a budget. Due to a decrease in state...Ch. 11.2 - Voting on an award for best restaurant. A group of...Ch. 11.2 - Use the following preference table for Exercises 9...Ch. 11.2 - Use the following preference table for Exercises 9...Ch. 11.2 - Complete the preference table so that the Borda...Ch. 11.2 - Complete the preference table so that A is the...Ch. 11.2 - Prob. 13ECh. 11.2 - Make a preference table similar to the one given...Ch. 11.2 - Complete the preference table so that the...Ch. 11.2 - Does the plurality method satisfy the majority...Ch. 11.2 - Does the plurality-with-elimination method satisfy...Ch. 11.2 - Prob. 18ECh. 11.2 - Presidential election. One of the several...Ch. 11.2 - Prob. 20ECh. 11.2 - Prob. 21ECh. 11.2 - A run off election. Repeat Exercise 21 using this...Ch. 11.2 - Prob. 23ECh. 11.2 - Prob. 24ECh. 11.2 - Prob. 25ECh. 11.2 - Prob. 26ECh. 11.2 - Prob. 27ECh. 11.2 - Voters are choosing among five options. Make a...Ch. 11.2 - Make a preference table, similar to the one given...Ch. 11.2 - Prob. 30ECh. 11.2 - Prob. 31ECh. 11.2 - Prob. 32ECh. 11.2 - Prob. 33ECh. 11.2 - Prob. 34ECh. 11.2 - One of the voting methods we have been discussing...Ch. 11.3 - Prob. 1ECh. 11.3 - Prob. 2ECh. 11.3 - In Exercises 1-12, the weight represent voters A,...Ch. 11.3 - Prob. 4ECh. 11.3 - Prob. 5ECh. 11.3 - Prob. 6ECh. 11.3 - In Exercises 1-12, the weight represent voters A,...Ch. 11.3 - In Exercises 1-12, the weight represent voters A,...Ch. 11.3 - In Exercises 1-12, the weight represent voters A,...Ch. 11.3 - Prob. 10ECh. 11.3 - Prob. 11ECh. 11.3 - Prob. 12ECh. 11.3 - In Exercises 13-16, write out all winning...Ch. 11.3 - Prob. 14ECh. 11.3 - In Exercises 13-16, write out all winning...Ch. 11.3 - Prob. 16ECh. 11.3 - Prob. 17ECh. 11.3 - Prob. 18ECh. 11.3 - Prob. 19ECh. 11.3 - Prob. 20ECh. 11.3 - Prob. 21ECh. 11.3 - Prob. 22ECh. 11.3 - Prob. 23ECh. 11.3 - Prob. 24ECh. 11.3 - Prob. 25ECh. 11.3 - Prob. 26ECh. 11.3 - Prob. 27ECh. 11.3 - Prob. 28ECh. 11.3 - Prob. 29ECh. 11.3 - Prob. 30ECh. 11.3 - Prob. 31ECh. 11.3 - Prob. 32ECh. 11.3 - In Exercises 29-34, determine the Banzhaf power...Ch. 11.3 - Prob. 34ECh. 11.3 - The system [3:1,1,1,1,1] is an example of a one...Ch. 11.3 - Prob. 36ECh. 11.3 - Consider the system [14:15,2,3,3,5] in which A is...Ch. 11.3 - Prob. 38ECh. 11.3 - Calculating power in the electoral college. After...Ch. 11.3 - Prob. 40ECh. 11.3 - Prob. 41ECh. 11.3 - Prob. 42ECh. 11.3 - Prob. 43ECh. 11.3 - In Example 5, we analyzed the voting power of the...Ch. 11.3 - In Example 5, we analyzed the voting power of the...Ch. 11.3 - Prob. 46ECh. 11.3 - Prob. 47ECh. 11.3 - Prob. 48ECh. 11.3 - Prob. 49ECh. 11.3 - Prob. 50ECh. 11.3 - A dummy in a weighted voting system is a voter...Ch. 11.3 - Prob. 52ECh. 11.3 - Prob. 53ECh. 11.3 - Prob. 54ECh. 11.3 - In Exercises 55 and 56, devise a voting system...Ch. 11.3 - Prob. 56ECh. 11.4 - In Exercises 1 4, use tree diagrams to find all...Ch. 11.4 - Prob. 2ECh. 11.4 - In Exercises 1 4, use tree diagrams to find all...Ch. 11.4 - Prob. 4ECh. 11.4 - Prob. 5ECh. 11.4 - Prob. 6ECh. 11.4 - Prob. 7ECh. 11.4 - Prob. 8ECh. 11.4 - Prob. 9ECh. 11.4 - Prob. 10ECh. 11.4 - Prob. 11ECh. 11.4 - Prob. 12ECh. 11.4 - In Exercises 1116, determine the Shapley-Shubik...Ch. 11.4 - Prob. 14ECh. 11.4 - Prob. 15ECh. 11.4 - Prob. 16ECh. 11.4 - The system [3:1,1,1,1,1] is an example of a one...Ch. 11.4 - Measuring power on a jury. We can consider a...Ch. 11.4 - Prob. 19ECh. 11.4 - Prob. 20ECh. 11.4 - Prob. 21ECh. 11.4 - Measuring power on a theater guild. The Theater...Ch. 11.4 - Measuring power on a state committee. The college...Ch. 11.4 - Prob. 24ECh. 11.4 - Prob. 25ECh. 11.4 - A new social media company, Chirp, has an...Ch. 11.4 - Prob. 27ECh. 11.4 - Measuring power among states. Repeat Exercise 27...Ch. 11.4 - Explain the difference between the Banzhaf index...Ch. 11.4 - Prob. 30ECh. 11.4 - Prob. 31ECh. 11.4 - Prob. 32ECh. 11.4 - Prob. 33ECh. 11.4 - Prob. 34ECh. 11.CR - Prob. 1CRCh. 11.CR - Prob. 2CRCh. 11.CR - Prob. 3CRCh. 11.CR - Prob. 4CRCh. 11.CR - Prob. 5CRCh. 11.CR - Prob. 6CRCh. 11.CR - Prob. 7CRCh. 11.CR - Prob. 8CRCh. 11.CR - Prob. 9CRCh. 11.CR - Prob. 10CRCh. 11.CR - Prob. 11CRCh. 11.CR - Prob. 12CRCh. 11.CR - Prob. 13CRCh. 11.CR - Prob. 14CRCh. 11.CR - Prob. 15CRCh. 11.CR - Prob. 16CRCh. 11.CR - Prob. 17CRCh. 11.CR - Prob. 18CRCh. 11.CT - Prob. 1CTCh. 11.CT - Prob. 2CTCh. 11.CT - Prob. 3CTCh. 11.CT - Prob. 4CTCh. 11.CT - Prob. 5CTCh. 11.CT - Prob. 6CTCh. 11.CT - Prob. 7CTCh. 11.CT - Prob. 8CTCh. 11.CT - Prob. 9CTCh. 11.CT - Determine the Banzhaf power index for each voter...Ch. 11.CT - Prob. 11CTCh. 11.CT - Prob. 12CTCh. 11.CT - Prob. 13CTCh. 11.CT - Prob. 14CTCh. 11.CT - Prob. 15CTCh. 11.CT - Prob. 16CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 6. [10 marks] Let T be a tree with n ≥ 2 vertices and leaves. Let BL(T) denote the block graph of T. (a) How many vertices does BL(T) have? (b) How many edges does BL(T) have? Prove that your answers are correct.arrow_forward4. [10 marks] Find both a matching of maximum size and a vertex cover of minimum size in the following bipartite graph. Prove that your answer is correct. ย ພarrow_forward5. [10 marks] Let G = (V,E) be a graph, and let X C V be a set of vertices. Prove that if |S||N(S)\X for every SCX, then G contains a matching M that matches every vertex of X (i.e., such that every x X is an end of an edge in M).arrow_forward
- Q/show that 2" +4 has a removable discontinuity at Z=2i Z(≥2-21)arrow_forwardRefer to page 100 for problems on graph theory and linear algebra. Instructions: • Analyze the adjacency matrix of a given graph to find its eigenvalues and eigenvectors. • Interpret the eigenvalues in the context of graph properties like connectivity or clustering. Discuss applications of spectral graph theory in network analysis. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 110 for problems on optimization. Instructions: Given a loss function, analyze its critical points to identify minima and maxima. • Discuss the role of gradient descent in finding the optimal solution. . Compare convex and non-convex functions and their implications for optimization. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 140 for problems on infinite sets. Instructions: • Compare the cardinalities of given sets and classify them as finite, countable, or uncountable. • Prove or disprove the equivalence of two sets using bijections. • Discuss the implications of Cantor's theorem on real-world computation. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 120 for problems on numerical computation. Instructions: • Analyze the sources of error in a given numerical method (e.g., round-off, truncation). • Compute the error bounds for approximating the solution of an equation. • Discuss strategies to minimize error in iterative methods like Newton-Raphson. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 145 for problems on constrained optimization. Instructions: • Solve an optimization problem with constraints using the method of Lagrange multipliers. • • Interpret the significance of the Lagrange multipliers in the given context. Discuss the applications of this method in machine learning or operations research. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Only 100% sure experts solve it correct complete solutions okarrow_forwardGive an example of a graph with at least 3 vertices that has exactly 2 automorphisms(one of which is necessarily the identity automorphism). Prove that your example iscorrect.arrow_forward3. [10 marks] Let Go (Vo, Eo) and G₁ = (V1, E1) be two graphs that ⚫ have at least 2 vertices each, ⚫are disjoint (i.e., Von V₁ = 0), ⚫ and are both Eulerian. Consider connecting Go and G₁ by adding a set of new edges F, where each new edge has one end in Vo and the other end in V₁. (a) Is it possible to add a set of edges F of the form (x, y) with x € Vo and y = V₁ so that the resulting graph (VUV₁, Eo UE₁ UF) is Eulerian? (b) If so, what is the size of the smallest possible F? Prove that your answers are correct.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License