Calculus: Special Edition: Chapters 1-5 (w/ WebAssign)
6th Edition
ISBN: 9781524908102
Author: SMITH KARL J, STRAUSS MONTY J, TODA MAGDALENA DANIELE
Publisher: Kendall Hunt Publishing
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 11.1, Problem 37PS
To determine
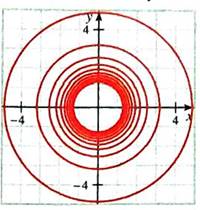
To match: The family of level curves for the equation
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Problem 1. An Apache helicopter of enemy is flying
along the path given by the curve f(x)=x2 + 7. A soldier,
placed at the point (1,2), wants to shoot the helicopter
when it is nearest to him. What is the nearest distance?
Help me, kindly solve it step by step
2. In submarine location problems, it is often important to find a submarine's closest point
of approach to a sonobuoy (a sound detector). Suppose that a submarine travels along a
parabolic path y = x² and the sonobuoy is at position (2, -0.5).
It has been known that the value of a needed to minimize the distance between the
submarine and the buoy must satisfy the following equation
1
1+x²
1
x=
Use Newton's Method to find a solution to the equation x =
9 decimal places.
1
1+x²
correct up to
Chapter 11 Solutions
Calculus: Special Edition: Chapters 1-5 (w/ WebAssign)
Ch. 11.1 - Prob. 1PSCh. 11.1 - Prob. 2PSCh. 11.1 - Prob. 3PSCh. 11.1 - Prob. 4PSCh. 11.1 - Prob. 5PSCh. 11.1 - Prob. 6PSCh. 11.1 - Prob. 7PSCh. 11.1 - Prob. 8PSCh. 11.1 - Prob. 9PSCh. 11.1 - Prob. 10PS
Ch. 11.1 - Prob. 11PSCh. 11.1 - Prob. 12PSCh. 11.1 - Prob. 13PSCh. 11.1 - Prob. 14PSCh. 11.1 - Prob. 15PSCh. 11.1 - Prob. 16PSCh. 11.1 - Prob. 17PSCh. 11.1 - Prob. 18PSCh. 11.1 - Prob. 19PSCh. 11.1 - Prob. 20PSCh. 11.1 - Prob. 21PSCh. 11.1 - Prob. 22PSCh. 11.1 - Prob. 23PSCh. 11.1 - Prob. 24PSCh. 11.1 - Prob. 25PSCh. 11.1 - Prob. 26PSCh. 11.1 - Prob. 27PSCh. 11.1 - Prob. 28PSCh. 11.1 - Prob. 29PSCh. 11.1 - Prob. 30PSCh. 11.1 - Prob. 31PSCh. 11.1 - Prob. 32PSCh. 11.1 - Prob. 33PSCh. 11.1 - Prob. 34PSCh. 11.1 - Prob. 35PSCh. 11.1 - Prob. 36PSCh. 11.1 - Prob. 37PSCh. 11.1 - Prob. 38PSCh. 11.1 - Prob. 39PSCh. 11.1 - Prob. 40PSCh. 11.1 - Prob. 41PSCh. 11.1 - Prob. 42PSCh. 11.1 - Prob. 43PSCh. 11.1 - Prob. 44PSCh. 11.1 - Prob. 45PSCh. 11.1 - Prob. 46PSCh. 11.1 - Prob. 47PSCh. 11.1 - Prob. 48PSCh. 11.1 - Prob. 49PSCh. 11.1 - Prob. 50PSCh. 11.1 - Prob. 51PSCh. 11.1 - Prob. 52PSCh. 11.1 - Prob. 53PSCh. 11.1 - Prob. 54PSCh. 11.1 - Prob. 55PSCh. 11.1 - Prob. 56PSCh. 11.1 - Prob. 57PSCh. 11.1 - Prob. 58PSCh. 11.1 - Prob. 59PSCh. 11.1 - Prob. 60PSCh. 11.2 - Prob. 1PSCh. 11.2 - Prob. 2PSCh. 11.2 - Prob. 3PSCh. 11.2 - Prob. 4PSCh. 11.2 - Prob. 5PSCh. 11.2 - Prob. 6PSCh. 11.2 - Prob. 7PSCh. 11.2 - Prob. 8PSCh. 11.2 - Prob. 9PSCh. 11.2 - Prob. 10PSCh. 11.2 - Prob. 11PSCh. 11.2 - Prob. 12PSCh. 11.2 - Prob. 13PSCh. 11.2 - Prob. 14PSCh. 11.2 - Prob. 15PSCh. 11.2 - Prob. 16PSCh. 11.2 - Prob. 17PSCh. 11.2 - Prob. 18PSCh. 11.2 - Prob. 19PSCh. 11.2 - Prob. 20PSCh. 11.2 - Prob. 21PSCh. 11.2 - Prob. 22PSCh. 11.2 - Prob. 23PSCh. 11.2 - Prob. 24PSCh. 11.2 - Prob. 25PSCh. 11.2 - Prob. 26PSCh. 11.2 - Prob. 27PSCh. 11.2 - Prob. 28PSCh. 11.2 - Prob. 29PSCh. 11.2 - Prob. 30PSCh. 11.2 - Prob. 31PSCh. 11.2 - Prob. 32PSCh. 11.2 - Prob. 33PSCh. 11.2 - Prob. 34PSCh. 11.2 - Prob. 35PSCh. 11.2 - Prob. 36PSCh. 11.2 - Prob. 37PSCh. 11.2 - Prob. 38PSCh. 11.2 - Prob. 39PSCh. 11.2 - Prob. 40PSCh. 11.2 - Prob. 41PSCh. 11.2 - Prob. 42PSCh. 11.2 - Prob. 43PSCh. 11.2 - Prob. 44PSCh. 11.2 - Prob. 45PSCh. 11.2 - Prob. 46PSCh. 11.2 - Prob. 47PSCh. 11.2 - Prob. 48PSCh. 11.2 - Prob. 49PSCh. 11.2 - Prob. 50PSCh. 11.2 - Prob. 51PSCh. 11.2 - Prob. 52PSCh. 11.2 - Prob. 53PSCh. 11.2 - Prob. 54PSCh. 11.2 - Prob. 55PSCh. 11.2 - Prob. 56PSCh. 11.2 - Prob. 57PSCh. 11.2 - Prob. 58PSCh. 11.2 - Prob. 59PSCh. 11.2 - Prob. 60PSCh. 11.3 - Prob. 1PSCh. 11.3 - Prob. 2PSCh. 11.3 - Prob. 3PSCh. 11.3 - Prob. 4PSCh. 11.3 - Prob. 5PSCh. 11.3 - Prob. 6PSCh. 11.3 - Prob. 7PSCh. 11.3 - Prob. 8PSCh. 11.3 - Prob. 9PSCh. 11.3 - Prob. 10PSCh. 11.3 - Prob. 11PSCh. 11.3 - Prob. 12PSCh. 11.3 - Prob. 13PSCh. 11.3 - Prob. 14PSCh. 11.3 - Prob. 15PSCh. 11.3 - Prob. 16PSCh. 11.3 - Prob. 17PSCh. 11.3 - Prob. 18PSCh. 11.3 - Prob. 19PSCh. 11.3 - Prob. 20PSCh. 11.3 - Prob. 21PSCh. 11.3 - Prob. 22PSCh. 11.3 - Prob. 23PSCh. 11.3 - Prob. 24PSCh. 11.3 - Prob. 25PSCh. 11.3 - Prob. 26PSCh. 11.3 - Prob. 27PSCh. 11.3 - Prob. 28PSCh. 11.3 - Prob. 29PSCh. 11.3 - Prob. 30PSCh. 11.3 - Prob. 31PSCh. 11.3 - Prob. 32PSCh. 11.3 - Prob. 33PSCh. 11.3 - Prob. 34PSCh. 11.3 - Prob. 35PSCh. 11.3 - Prob. 36PSCh. 11.3 - Prob. 37PSCh. 11.3 - Prob. 38PSCh. 11.3 - Prob. 39PSCh. 11.3 - Prob. 40PSCh. 11.3 - Prob. 41PSCh. 11.3 - Prob. 42PSCh. 11.3 - Prob. 43PSCh. 11.3 - Prob. 44PSCh. 11.3 - Prob. 45PSCh. 11.3 - Prob. 46PSCh. 11.3 - Prob. 47PSCh. 11.3 - Prob. 48PSCh. 11.3 - Prob. 49PSCh. 11.3 - Prob. 50PSCh. 11.3 - Prob. 51PSCh. 11.3 - Prob. 52PSCh. 11.3 - Prob. 53PSCh. 11.3 - Prob. 54PSCh. 11.3 - Prob. 55PSCh. 11.3 - Prob. 56PSCh. 11.3 - Prob. 57PSCh. 11.3 - Prob. 58PSCh. 11.3 - Prob. 59PSCh. 11.3 - Prob. 60PSCh. 11.4 - Prob. 1PSCh. 11.4 - Prob. 2PSCh. 11.4 - Prob. 3PSCh. 11.4 - Prob. 4PSCh. 11.4 - Prob. 5PSCh. 11.4 - Prob. 6PSCh. 11.4 - Prob. 7PSCh. 11.4 - Prob. 8PSCh. 11.4 - Prob. 9PSCh. 11.4 - Prob. 10PSCh. 11.4 - Prob. 11PSCh. 11.4 - Prob. 12PSCh. 11.4 - Prob. 13PSCh. 11.4 - Prob. 14PSCh. 11.4 - Prob. 15PSCh. 11.4 - Prob. 16PSCh. 11.4 - Prob. 17PSCh. 11.4 - Prob. 18PSCh. 11.4 - Prob. 19PSCh. 11.4 - Prob. 20PSCh. 11.4 - Prob. 21PSCh. 11.4 - Prob. 22PSCh. 11.4 - Prob. 23PSCh. 11.4 - Prob. 24PSCh. 11.4 - Prob. 25PSCh. 11.4 - Prob. 26PSCh. 11.4 - Prob. 27PSCh. 11.4 - Prob. 28PSCh. 11.4 - Prob. 29PSCh. 11.4 - Prob. 30PSCh. 11.4 - Prob. 31PSCh. 11.4 - Prob. 32PSCh. 11.4 - Prob. 33PSCh. 11.4 - Prob. 34PSCh. 11.4 - Prob. 35PSCh. 11.4 - Prob. 36PSCh. 11.4 - Prob. 37PSCh. 11.4 - Prob. 38PSCh. 11.4 - Prob. 39PSCh. 11.4 - Prob. 40PSCh. 11.4 - Prob. 41PSCh. 11.4 - Prob. 42PSCh. 11.4 - Prob. 43PSCh. 11.4 - Prob. 44PSCh. 11.4 - Prob. 45PSCh. 11.4 - Prob. 46PSCh. 11.4 - Prob. 47PSCh. 11.4 - Prob. 48PSCh. 11.4 - Prob. 49PSCh. 11.4 - Prob. 50PSCh. 11.4 - Prob. 51PSCh. 11.4 - Prob. 52PSCh. 11.4 - Prob. 53PSCh. 11.4 - Prob. 54PSCh. 11.4 - Prob. 55PSCh. 11.4 - Prob. 56PSCh. 11.4 - Prob. 57PSCh. 11.4 - Prob. 58PSCh. 11.4 - Prob. 59PSCh. 11.4 - Prob. 60PSCh. 11.5 - Prob. 1PSCh. 11.5 - Prob. 2PSCh. 11.5 - Prob. 3PSCh. 11.5 - Prob. 4PSCh. 11.5 - Prob. 5PSCh. 11.5 - Prob. 6PSCh. 11.5 - Prob. 7PSCh. 11.5 - Prob. 8PSCh. 11.5 - Prob. 9PSCh. 11.5 - Prob. 10PSCh. 11.5 - Prob. 11PSCh. 11.5 - Prob. 12PSCh. 11.5 - Prob. 13PSCh. 11.5 - Prob. 14PSCh. 11.5 - Prob. 15PSCh. 11.5 - Prob. 16PSCh. 11.5 - Prob. 17PSCh. 11.5 - Prob. 18PSCh. 11.5 - Prob. 19PSCh. 11.5 - Prob. 20PSCh. 11.5 - Prob. 21PSCh. 11.5 - Prob. 22PSCh. 11.5 - Prob. 23PSCh. 11.5 - Prob. 24PSCh. 11.5 - Prob. 25PSCh. 11.5 - Prob. 26PSCh. 11.5 - Prob. 27PSCh. 11.5 - Prob. 28PSCh. 11.5 - Prob. 29PSCh. 11.5 - Prob. 30PSCh. 11.5 - Prob. 31PSCh. 11.5 - Prob. 32PSCh. 11.5 - Prob. 33PSCh. 11.5 - Prob. 34PSCh. 11.5 - Prob. 35PSCh. 11.5 - Prob. 36PSCh. 11.5 - Prob. 37PSCh. 11.5 - Prob. 38PSCh. 11.5 - Prob. 39PSCh. 11.5 - Prob. 40PSCh. 11.5 - Prob. 41PSCh. 11.5 - Prob. 42PSCh. 11.5 - Prob. 43PSCh. 11.5 - Prob. 44PSCh. 11.5 - Prob. 45PSCh. 11.5 - Prob. 46PSCh. 11.5 - Prob. 47PSCh. 11.5 - Prob. 48PSCh. 11.5 - Prob. 49PSCh. 11.5 - Prob. 50PSCh. 11.5 - Prob. 51PSCh. 11.5 - Prob. 52PSCh. 11.5 - Prob. 53PSCh. 11.5 - Prob. 54PSCh. 11.5 - Prob. 55PSCh. 11.5 - Prob. 56PSCh. 11.5 - Prob. 57PSCh. 11.5 - Prob. 58PSCh. 11.5 - Prob. 59PSCh. 11.5 - Prob. 60PSCh. 11.6 - Prob. 1PSCh. 11.6 - Prob. 2PSCh. 11.6 - Prob. 3PSCh. 11.6 - Prob. 4PSCh. 11.6 - Prob. 5PSCh. 11.6 - Prob. 6PSCh. 11.6 - Prob. 7PSCh. 11.6 - Prob. 8PSCh. 11.6 - Prob. 9PSCh. 11.6 - Prob. 10PSCh. 11.6 - Prob. 11PSCh. 11.6 - Prob. 12PSCh. 11.6 - Prob. 13PSCh. 11.6 - Prob. 14PSCh. 11.6 - Prob. 15PSCh. 11.6 - Prob. 16PSCh. 11.6 - Prob. 17PSCh. 11.6 - Prob. 18PSCh. 11.6 - Prob. 19PSCh. 11.6 - Prob. 20PSCh. 11.6 - Prob. 21PSCh. 11.6 - Prob. 22PSCh. 11.6 - Prob. 23PSCh. 11.6 - Prob. 24PSCh. 11.6 - Prob. 25PSCh. 11.6 - Prob. 26PSCh. 11.6 - Prob. 27PSCh. 11.6 - Prob. 28PSCh. 11.6 - Prob. 29PSCh. 11.6 - Prob. 30PSCh. 11.6 - Prob. 31PSCh. 11.6 - Prob. 32PSCh. 11.6 - Prob. 33PSCh. 11.6 - Prob. 34PSCh. 11.6 - Prob. 35PSCh. 11.6 - Prob. 36PSCh. 11.6 - Prob. 37PSCh. 11.6 - Prob. 38PSCh. 11.6 - Prob. 39PSCh. 11.6 - Prob. 40PSCh. 11.6 - Prob. 41PSCh. 11.6 - Prob. 42PSCh. 11.6 - Prob. 43PSCh. 11.6 - Prob. 44PSCh. 11.6 - Prob. 45PSCh. 11.6 - Prob. 46PSCh. 11.6 - Prob. 47PSCh. 11.6 - Prob. 48PSCh. 11.6 - Prob. 49PSCh. 11.6 - Prob. 50PSCh. 11.6 - Prob. 51PSCh. 11.6 - Prob. 52PSCh. 11.6 - Prob. 53PSCh. 11.6 - Prob. 54PSCh. 11.6 - Prob. 55PSCh. 11.6 - Prob. 56PSCh. 11.6 - Prob. 57PSCh. 11.6 - Prob. 58PSCh. 11.6 - Prob. 59PSCh. 11.6 - Prob. 60PSCh. 11.7 - Prob. 1PSCh. 11.7 - Prob. 2PSCh. 11.7 - Prob. 3PSCh. 11.7 - Prob. 4PSCh. 11.7 - Prob. 5PSCh. 11.7 - Prob. 6PSCh. 11.7 - Prob. 7PSCh. 11.7 - Prob. 8PSCh. 11.7 - Prob. 9PSCh. 11.7 - Prob. 10PSCh. 11.7 - Prob. 11PSCh. 11.7 - Prob. 12PSCh. 11.7 - Prob. 13PSCh. 11.7 - Prob. 14PSCh. 11.7 - Prob. 15PSCh. 11.7 - Prob. 16PSCh. 11.7 - Prob. 17PSCh. 11.7 - Prob. 18PSCh. 11.7 - Prob. 19PSCh. 11.7 - Prob. 20PSCh. 11.7 - Prob. 21PSCh. 11.7 - Prob. 22PSCh. 11.7 - Prob. 23PSCh. 11.7 - Prob. 24PSCh. 11.7 - Prob. 25PSCh. 11.7 - Prob. 26PSCh. 11.7 - Prob. 27PSCh. 11.7 - Prob. 28PSCh. 11.7 - Prob. 29PSCh. 11.7 - Prob. 30PSCh. 11.7 - Prob. 31PSCh. 11.7 - Prob. 32PSCh. 11.7 - Prob. 33PSCh. 11.7 - Prob. 34PSCh. 11.7 - Prob. 35PSCh. 11.7 - Prob. 36PSCh. 11.7 - Prob. 37PSCh. 11.7 - Prob. 38PSCh. 11.7 - Prob. 39PSCh. 11.7 - Prob. 40PSCh. 11.7 - Prob. 41PSCh. 11.7 - Prob. 42PSCh. 11.7 - Prob. 43PSCh. 11.7 - Prob. 44PSCh. 11.7 - Prob. 45PSCh. 11.7 - Prob. 46PSCh. 11.7 - Prob. 47PSCh. 11.7 - Prob. 48PSCh. 11.7 - Prob. 49PSCh. 11.7 - Prob. 50PSCh. 11.7 - Prob. 51PSCh. 11.7 - Prob. 52PSCh. 11.7 - Prob. 53PSCh. 11.7 - Prob. 54PSCh. 11.7 - Prob. 55PSCh. 11.7 - Prob. 56PSCh. 11.7 - Prob. 57PSCh. 11.7 - Prob. 58PSCh. 11.7 - Prob. 59PSCh. 11.7 - Prob. 60PSCh. 11.8 - Prob. 1PSCh. 11.8 - Prob. 2PSCh. 11.8 - Prob. 3PSCh. 11.8 - Prob. 4PSCh. 11.8 - Prob. 5PSCh. 11.8 - Prob. 6PSCh. 11.8 - Prob. 7PSCh. 11.8 - Prob. 8PSCh. 11.8 - Prob. 9PSCh. 11.8 - Prob. 10PSCh. 11.8 - Prob. 11PSCh. 11.8 - Prob. 12PSCh. 11.8 - Prob. 13PSCh. 11.8 - Prob. 14PSCh. 11.8 - Prob. 15PSCh. 11.8 - Prob. 16PSCh. 11.8 - Prob. 17PSCh. 11.8 - Prob. 18PSCh. 11.8 - Prob. 19PSCh. 11.8 - Prob. 20PSCh. 11.8 - Prob. 21PSCh. 11.8 - Prob. 22PSCh. 11.8 - Prob. 23PSCh. 11.8 - Prob. 24PSCh. 11.8 - Prob. 25PSCh. 11.8 - Prob. 26PSCh. 11.8 - Prob. 27PSCh. 11.8 - Prob. 28PSCh. 11.8 - Prob. 29PSCh. 11.8 - Prob. 30PSCh. 11.8 - Prob. 31PSCh. 11.8 - Prob. 32PSCh. 11.8 - Prob. 33PSCh. 11.8 - Prob. 34PSCh. 11.8 - Prob. 35PSCh. 11.8 - Prob. 36PSCh. 11.8 - Prob. 37PSCh. 11.8 - Prob. 38PSCh. 11.8 - Prob. 39PSCh. 11.8 - Prob. 40PSCh. 11.8 - Prob. 41PSCh. 11.8 - Prob. 42PSCh. 11.8 - Prob. 43PSCh. 11.8 - Prob. 44PSCh. 11.8 - Prob. 45PSCh. 11.8 - Prob. 46PSCh. 11.8 - Prob. 47PSCh. 11.8 - Prob. 48PSCh. 11.8 - Prob. 49PSCh. 11.8 - Prob. 50PSCh. 11.8 - Prob. 51PSCh. 11.8 - Prob. 52PSCh. 11.8 - Prob. 53PSCh. 11.8 - Prob. 54PSCh. 11.8 - Prob. 55PSCh. 11.8 - Prob. 56PSCh. 11.8 - Prob. 57PSCh. 11.8 - Prob. 58PSCh. 11.8 - Prob. 59PSCh. 11.8 - Prob. 60PSCh. 11 - Prob. 1PECh. 11 - Prob. 2PECh. 11 - Prob. 3PECh. 11 - Prob. 4PECh. 11 - Prob. 5PECh. 11 - Prob. 6PECh. 11 - Prob. 7PECh. 11 - Prob. 8PECh. 11 - Prob. 9PECh. 11 - Prob. 10PECh. 11 - Prob. 11PECh. 11 - Prob. 12PECh. 11 - Prob. 13PECh. 11 - Prob. 14PECh. 11 - Prob. 15PECh. 11 - Prob. 16PECh. 11 - Prob. 17PECh. 11 - Prob. 18PECh. 11 - Prob. 19PECh. 11 - Prob. 20PECh. 11 - Prob. 21PECh. 11 - Prob. 22PECh. 11 - Prob. 23PECh. 11 - Prob. 24PECh. 11 - Prob. 25PECh. 11 - Prob. 26PECh. 11 - Prob. 27PECh. 11 - Prob. 28PECh. 11 - Prob. 29PECh. 11 - Prob. 30PECh. 11 - Prob. 1SPCh. 11 - Prob. 2SPCh. 11 - Prob. 3SPCh. 11 - Prob. 4SPCh. 11 - Prob. 5SPCh. 11 - Prob. 6SPCh. 11 - Prob. 7SPCh. 11 - Prob. 8SPCh. 11 - Prob. 9SPCh. 11 - Prob. 10SPCh. 11 - Prob. 11SPCh. 11 - Prob. 12SPCh. 11 - Prob. 13SPCh. 11 - Prob. 14SPCh. 11 - Prob. 15SPCh. 11 - Prob. 16SPCh. 11 - Prob. 17SPCh. 11 - Prob. 18SPCh. 11 - Prob. 19SPCh. 11 - Prob. 20SPCh. 11 - Prob. 21SPCh. 11 - Prob. 22SPCh. 11 - Prob. 23SPCh. 11 - Prob. 24SPCh. 11 - Prob. 25SPCh. 11 - Prob. 26SPCh. 11 - Prob. 27SPCh. 11 - Prob. 28SPCh. 11 - Prob. 29SPCh. 11 - Prob. 30SPCh. 11 - Prob. 31SPCh. 11 - Prob. 32SPCh. 11 - Prob. 33SPCh. 11 - Prob. 34SPCh. 11 - Prob. 35SPCh. 11 - Prob. 36SPCh. 11 - Prob. 37SPCh. 11 - Prob. 38SPCh. 11 - Prob. 39SPCh. 11 - Prob. 40SPCh. 11 - Prob. 41SPCh. 11 - Prob. 42SPCh. 11 - Prob. 43SPCh. 11 - Prob. 44SPCh. 11 - Prob. 45SPCh. 11 - Prob. 46SPCh. 11 - Prob. 47SPCh. 11 - Prob. 48SPCh. 11 - Prob. 49SPCh. 11 - Prob. 50SPCh. 11 - Prob. 51SPCh. 11 - Prob. 52SPCh. 11 - Prob. 53SPCh. 11 - Prob. 54SPCh. 11 - Prob. 55SPCh. 11 - Prob. 56SPCh. 11 - Prob. 57SPCh. 11 - Prob. 58SPCh. 11 - Prob. 59SPCh. 11 - Prob. 60SPCh. 11 - Prob. 61SPCh. 11 - Prob. 62SPCh. 11 - Prob. 63SPCh. 11 - Prob. 64SPCh. 11 - Prob. 65SPCh. 11 - Prob. 66SPCh. 11 - Prob. 67SPCh. 11 - Prob. 68SPCh. 11 - Prob. 69SPCh. 11 - Prob. 70SPCh. 11 - Prob. 71SPCh. 11 - Prob. 72SPCh. 11 - Prob. 73SPCh. 11 - Prob. 74SPCh. 11 - Prob. 75SPCh. 11 - Prob. 76SPCh. 11 - Prob. 77SPCh. 11 - Prob. 78SPCh. 11 - Prob. 79SPCh. 11 - Prob. 80SPCh. 11 - Prob. 81SPCh. 11 - Prob. 82SPCh. 11 - Prob. 83SPCh. 11 - Prob. 84SPCh. 11 - Prob. 85SPCh. 11 - Prob. 86SPCh. 11 - Prob. 87SPCh. 11 - Prob. 88SPCh. 11 - Prob. 89SPCh. 11 - Prob. 90SPCh. 11 - Prob. 91SPCh. 11 - Prob. 92SPCh. 11 - Prob. 93SPCh. 11 - Prob. 94SPCh. 11 - Prob. 95SPCh. 11 - Prob. 96SPCh. 11 - Prob. 97SPCh. 11 - Prob. 98SPCh. 11 - Prob. 99SP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 10. Consider a parabola y = x² and a circle with center C(0,2), as shown below. The points A and B are special points where the parabola and circle are mutually tangential. -1 3 2 B (a) Let (x, y) be a point on the parabola, where x 0. Demonstrate the line from (x, y) which also passes through the center of the circle must have a slope of x² - 2 COS I (b) Let (b, b²) be the coordinates of B, the rightmost point of tangency. A special fact about the parabola y = x² is that its slope at a point (x, y) is always given by the formula m = 2x, so at x = b, the slope is 2b. Use this, along with your result from (a) to determine the value of these coordinates of B. Now determine an equation for the tangent line to the circle at B. Also, sketch a picture of this situation. Show your tangent line, the circle, and parabola all on one graph. (d) The normal line through a point is always perpendicular to the tangent line through that same point. Determine an equation for the normal line to the…arrow_forwardConsider the 2 implicitly-defined curves 5x + 2y + x³ + xy² 3 0 and 4 2x 5y + y² – xy² 0. Plot these 2 functions on the same graph. Notice that it appears as though they intersect at a right angle at the origin. For this discussion post, you will figure out (using Calculus) whether or not these 2 functions actually intersect at a right angle. You do not need to include a graph in your post, but you must explain your answer fully. — - =arrow_forward1 3. Show that y = x and y have tangent lines that are perpendicular. (Remember that perpendicular lines have slopes %3D - that are negative reciprocals of one another.)arrow_forward
- (1) Draw contour plots for the following functions. Your contour plot must include at least 6 level curves (contours) including positive and negative values for the level k. (i) ƒ(x, y) = x²y (2) For the function in part (i) of the previous problem, draw vertical cross-sections of its graph at x = k and y = k for at least 5 values of k.arrow_forwardDetermine the compromised areas between the given curves and lines. f(x) = x² -2x +1, x = -1, x = 3arrow_forwardProblem 3. Compute fF.dr along the specified curves. F(x, y) = (1 + x², xy²) (a) curve: from 0 to Q, along line segment PQ (b) curve: from 0 to Q, along segments OP and PQ y Q(2,3) P(0,3) Vy Answer: Answer:arrow_forward
- A certain factory using x do-dads and y widgets per hour will produce:T(x, y) = 60x2 + y thingamabobs per day.Describe the relationship between inputs x and y such that 3000 thingamabobs are produced per day. (That is, find the level curve of T corresponding to T = 3000.) (A) y = 1 50x2 (B) y = x2 50 (C) y = 60(x2 − 50) (D) y = 60(50 − x2) (E) y = 3000x2 (F) y = 60(50 + x2) (G) y = 50 x2 (H) y = 50x2arrow_forward2. A simple curve that often makes a good model for the variable costs of a company, as a function of the number of units produced, x, has the form: y = b₁x + b₂x² + b3x³. (There is no constant term because fixed costs are not included.) Consider the following table of recorded variable costs versus units produced for some company:arrow_forward4. Given the equation 2y2 – 2xy – 4y + x2 = 0 of a curve, obtain the x-coordinates of each point at which the curve has a horizontal tangent.arrow_forward
- Can you please solve these two sub problem and show all of the steps and say the correct letterarrow_forward3. Draw contour maps of each of the following functions, choosing appropriate an appropriate contour interval and showing at least 6 level curves. (a) f(x, y) = x² y² + 4 9 (b) g(x, y) = exp (c) h(x, y) = 3x -y +2.arrow_forward6. The graph of y = x° is graphed in blue. Which of the following equations could be equation of the function graphed in red? 1 y = 20 (2 – 2)* +1 1 y = 20 (x + 2)* +1 y = 20 (z – 2)° +1 O y=20 (z +2)° + 1 a bottom right b bottom left top left d top rightarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Chain Rule dy:dx = dy:du*du:dx; Author: Robert Cappetta;https://www.youtube.com/watch?v=IUYniALwbHs;License: Standard YouTube License, CC-BY
CHAIN RULE Part 1; Author: Btech Maths Hub;https://www.youtube.com/watch?v=TIAw6AJ_5Po;License: Standard YouTube License, CC-BY