
Concept explainers
BIO Correcting Torsiversion
Torsiversion is a medical condition in which a tooth is rotated away from its normal position about the long axis of the root Studies show that about 2 percent of the population suffer from this condition to some degree. For those who do, the improper alignment of the tooth can lead to tooth-to-tooth collisions during eating, as well as other problems. Typical patients display a rotation ranging from 20° to 60°, with an average around 30°.
An example is shown in Figure 11-69 (a), where the first premolar is not only displaced slightly from its proper location in the negative y direction, but also rotated clockwise from its normal orientation. To correct this condition an orthodontist might use an archwire and a bracket to apply both a force and a torque to the tooth. In the simplest case, two forces are applied to the tooth in different locations, as indicated by F1 and F2 in Figure 11-69 (a). These two forces, if chosen properly, can reposition the tooth by exerting a net force in the positive y direction, and also reorient it by applying a torque in the counterclockwise direction.
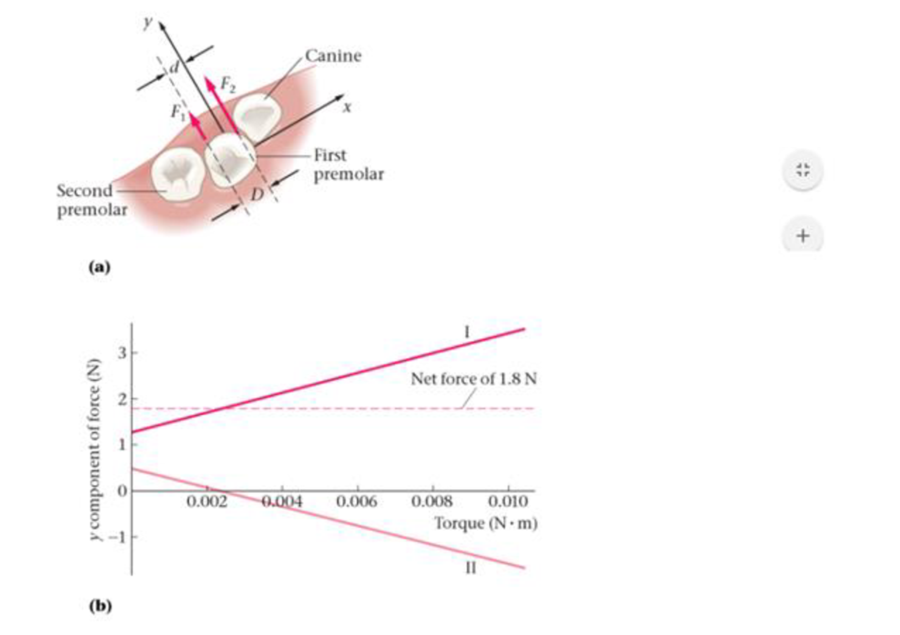
Figure 11-69 Problems 92, 93, 94, and 95
In a typical case it may be desired to have a net force in the positive y direction of 1.8 N. In addition, the distances in Figure 11-69 (a) can be taken to be d = 3.2 mm and D = 4.5 mm. Given these conditions, a range of torques is possible for various values of the y components of the forces, F1y and F2y. For example Figure 11-69 (b) shows the values of F1y and F2y necessary to produce a given torque, where the torque is measured about the center of the tooth (which is also the origin of the coordinate system). Notice that the two forces always add to 1.8 N in the positive y direction, though one of the forces changes sign as the torque is increased.
94. •• Find the values of F1y and F2y required to give zero net torque.
- A. F1y = −1.2 N, F2y = 3.0 N
- B. F1y = 1.1 N, F2y = 0.75 N
- C. F1y = −0.73 N, F2y = 2.5 N
- D. F1y = −0.52 N, F2y = 1.3N
Want to see the full answer?
Check out a sample textbook solution
Chapter 11 Solutions
Physics (5th Edition)
Additional Science Textbook Solutions
University Physics (14th Edition)
An Introduction to Thermal Physics
Conceptual Physics (12th Edition)
Life in the Universe (4th Edition)
Physics for Scientists and Engineers: A Strategic Approach with Modern Physics (4th Edition)
College Physics: A Strategic Approach (3rd Edition)
- Problems 62 and 63 are paired. 62. C A disk is rotating around a fixed axis that passes through its center and is perpendicular to the face of the disk. Consider a point on the rim of the disk (point R) and another point halfway between the center and the rim (point H) at one particular instant. a. How does the angular speed v of the disk at point H compare with the angular speed of the disk at point R? b. How does the tangential speed of the disk at point H compare with the tangential speed of the disk at point R? c. Suppose we pick a point H on the disk at random (by throwing a dart, for example), and we compare the speeds at that point with the speeds at point R. How will the answers to parts (a) and (b) be different? Explain.arrow_forwardA uniform cylindrical grindstion has a mass of 10 kg and a radius of 12 cm. (a) What is the rotational kinetic energy of the grindstone when it is rotating at 1.5103rev/min ? (b) After the grindstone’s motor is turned off, a knife blade is pressed against the outer edge coefficient of kinetic friction between the grindstone and the blade is 0.80. Use the work energy theorem to determine how many turns the grindstone makes before it stops.arrow_forwardAdditional Problems A typical propeller of a turbine used to generate electricity from the wind consists of three blades as in Figure P8.75. Each blade has a length of L = 35 in and a mass of m = 420 kg. The propeller rotates at the rate of 25 rev/min. (a) Convert the angular speed of the propeller to units of rad/s. Find (b) the moment of inertia of the propeller about the axis of rotation and (c) the total kinetic, energy of the propeller. Figure P8.75arrow_forward
- The dung beetle is known as one of the strongest animals for its size, often forming balls of dung up to 10 times their own mass and rolling them to locations where they can be buried and stored as food. A typical dung ball formed by the species K. nigroaeneus has a radius of 2.00 cm and is rolled by the beetle at 6.25 cm/s. (a) What is the rolling balls angular speed? (b) How many full rotations are required if the beetle rolls the ball a distance of 1.00 m?arrow_forwardAn electric sander consisting of a rotating disk of mass 0.7 kg and radius 10 cm rotates at 15 rev/sec. When applied to a rough wooden wall the rotation rate decreases by 20 . (a) What is the final rotational kinetic energy of the rotating disk? (a) How much has its rotational kinetic energy decreased?arrow_forwardOne method of pitching a softball is called the wind-mill delivery method, in which the pitchers arm rotates through approximately 360 in a vertical plane before the 198-gram ball is released at the lowest point of the circular motion. An experienced pitcher can throw a ball with a speed of 98.0 mi/h. Assume the angular acceleration is uniform throughout the pitching motion and take the distance between the softball and the shoulder joint to be 74.2 cm. (a) Determine the angular speed of the arm in rev/s at the instant of release, (b) Find the value of the angular acceleration in rev/s2 and the radial and tangential acceleration of the ball just before it is released, (c) Determine the force exerted on the ball by the pitchers hand (both radial and tangential components) just before it is released.arrow_forward
- A pulsar is a rapidly rotating neutron star. The Crab nebula pulsar in the constellation Taurus has a period of 33.510-3s , radius 10.0 km, and mass 2.81030kg . The pulsar’s rotational period will increase over time due to the release of electromagnetic radiation, which doesn’t change its radius but reduces its rotational energy. (a) What is the angular momentum of the pulsar? (b) Suppose the angular velocity decreases at a rate of 1014rad/s2 . What is the torque on the pulsar?arrow_forwardAs a compact disc (CD) spins clockwise as seen from above,information is read from it, starting with the innermost ring andmoving outward. When the information is being read from theinnermost ring, the CDs angular speed is 0 = 52.4 rad /s. TheCD slows down so that when information is read from the outermost ring, = 20.9 rad /s. It takes 74 min 33 s to read themusic from a particular CD. Find the constant angular acceleration of the CD.arrow_forwardWhile punting a football, a kicker rotates his leg about the hip joint. The moment of inertia of the leg is 3.75kg-m2 and its rotational kinetic energy is 175 J. (a) What is the angular velocity of the leg? (b) What is the velocity of tip of the punter's shoe if it is 1.05 m from the hip joint? (c) Explain how the football can be given a velocity greater than the tip of the shoe (necessary for a decent kick distance).arrow_forward
- To find the total angular displacement during the playing time of the compact disc in part (B) of Example 10.2, the disc was modeled as a rigid object under constant angular acceleration. In reality, the angular acceleration of a disc is not constant. In this problem, let us explore the actual time dependence of the angular acceleration. (a) Assume the track on the disc is a spiral such that adjacent loops of the track are separated by a small distance h. Slum that the radius r of a given portion of the track is given by r=ri+h2 where ri is the radius of the innermost portion of the track and is the angle through which the disc turns to arrive at the location of the track of radius r. (b) Show that the rate of change of the angle is given by ddt=vri+(h/2) where v is the constant speed with which the disc surface passes the laser. (c) From the result in part (b), use integration to find an expression for the angle as a function of time. (d) From the result in part (c), use differentiation to find the angular acceleration of the disc as a function of time.arrow_forwardThe angular velocity of a flywheel with radius 1.0 m varies according to (t)=2.0t . Plot ac(t) and at(t) from t=0 to 3.0 s for r=1.0m . Analyze these results to explain when acat and when acat for a point on the flywheel at a radius of 1.0 m.arrow_forwardWhile punting a football, a kicker rotates his leg about the hip joint. The moment of inertia of the leg is 3.75kgm2 and its rotational kinetic energy is 175 J. (a) What is the angular velocity of the leg? (b) What is the velocity of tip of the punter’s shoe if it is 1.05 m from the hip joint?arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





